Introducción a las ecuaciones diferenciales

Aplicaciones que llevan a ecuaciones diferenciales

En aplicaciones de física e ingeniería, a menudo consideramos las fuerzas que actúan sobre un objeto, y usamos esta información para comprender el movimiento resultante que puede ocurrir. Por ejemplo, si comenzamos con un objeto en la superficie de la Tierra, la fuerza primaria que actúa sobre ese objeto es la gravedad. Los físicos e ingenieros pueden usar esta información, junto con la segunda ley de movimiento de Newton (en forma de ecuación F = ma, donde F representa la fuerza, m representa la masa y a representa la aceleración), para deducir una ecuación que se pueda resolver.

Nuestro objetivo es hallar la velocidad v(t) en cualquier momento t. Para hacer esto, configuramos un problema de valor inicial. Supongamos que la masa de la pelota es m, donde m se mide en kilogramos. Usamos la segunda ley de Newton, que establece que la fuerza que actúa sobre un objeto es igual a su masa multiplicada por su aceleración (F = ma). La aceleración es la derivada de la velocidad, entonces a(t) = v′(t). Por lo tanto, la fuerza que actúa sobre la pelota de béisbol está dada por F = mv′(t). Sin embargo, esta fuerza debe ser igual a la fuerza de gravedad que actúa sobre el objeto, que (nuevamente usando la segunda ley de Newton) viene dada por F_g = −mg, ya que esta fuerza actúa en dirección descendente. Por lo tanto, obtenemos la ecuación F = F_g, que se convierte en mv′(t) = – mg. Dividir ambos lados de la ecuación por m da la ecuación

v′(t) = – g. 

Tenga en cuenta que esta ecuación diferencial sigue siendo la misma independientemente de la masa del objeto.

Ahora necesitamos un valor inicial. Debido a que estamos calculando la velocidad, tiene sentido en el contexto del problema suponer que conocemos la velocidad inicial, o la velocidad en el tiempo t = 0. Esto se denota por v(0) = v₀.

EJEMPLO ILUSTRATIVO 9.1_6. Velocidad de una pelota de béisbol en movimiento

Se lanza una pelota de béisbol hacia arriba desde una altura de 3 metros sobre la superficie de la Tierra con una velocidad inicial de 10 m/s, y la única fuerza que actúa sobre ella es la gravedad. La pelota tiene una masa de 0.15 kg en la superficie de la Tierra.
a. Encuentre la velocidad v(t) de la pelota de béisbol en el tiempo t.
b. ¿Cuál es su velocidad después de 2 segundos?

Solución:
a. De la discusión anterior, la ecuación diferencial que se aplica en esta situación es

donde g = 9.8 m/s². La condición inicial es v(0) = v₀, donde v₀ = 10 m/s. Por lo tanto, el problema del valor inicial es v′(t) = – m/s², v(0) = 10 m/s.
El primer paso para resolver este problema de valor inicial es tomar la antiderivada de ambos lados de la ecuación diferencial. Esto da

El siguiente paso es resolver C. Para hacer esto, sustituya t = 0 y v(0) = 10 en la ecuación anterior y despeje C:

Por lo tanto, C = 10, por lo que la función de velocidad viene dada por v(t) = – 9.8t + 10.

b. Para encontrar la velocidad después de 2 segundos, sustituya t = 2 en v(t),

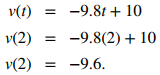
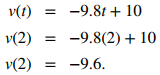
Las unidades de velocidad son metros por segundo. Como la respuesta es negativa, el objeto está cayendo a una velocidad de 9,6 m/s. ◊

Una pregunta natural después de resolver este tipo de problemas es qué tan alto estará el objeto sobre la superficie de la Tierra en un momento dado. Supongamos que s(t) denota la altura sobre la superficie de la Tierra del objeto, medida en metros. Como la velocidad es la derivada de la posición (en este caso, la altura), esta suposición da la ecuación s′(t) = v(t). Un valor inicial es necesario; en este caso la altura inicial del objeto funciona bien. Deje que la altura inicial esté dada por la ecuación s(0) = so. Juntos, estos supuestos dan el problema del valor inicial

s′(t) = v(t), s(0) = so. 

Si se conoce la función de velocidad, entonces también es posible resolver la función de posición.

EJEMPLO ILUSTRATIVO 9.1_7. Altura de una pelota de béisbol en movimiento

Se lanza una pelota de béisbol hacia arriba desde una altura de 3 metros sobre la superficie de la Tierra con una velocidad inicial de 10 m/s, y la única fuerza que actúa sobre ella es la gravedad. La pelota tiene una masa de 0,15 kilogramos en la superficie de la Tierra.
a. Encuentre la posición s(t) del béisbol en el tiempo t.
b. ¿Cuál es su altura después de 2 segundos?

Solución:
a. Ya sabemos que la función de velocidad para este problema es v(t) = – 9.8t + 10. La altura inicial de la pelota de béisbol es de 3 metros, por lo que so = 3. Por lo tanto, el problema del valor inicial para este ejemplo es

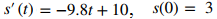
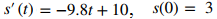
Para resolver el problema del valor inicial, primero encontramos las antiderivadas:

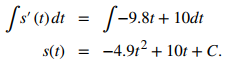
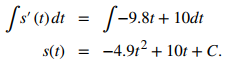
A continuación, sustituimos t = 0 y resolvemos C:

Por lo tanto, la función de posición es s(t) = – 4.9t² + 10t + 3.

b. La altura de la pelota de béisbol después de 2s viene dada por s(2):

Por lo tanto, la pelota de béisbol está a 3.4 metros sobre la superficie de la Tierra después de 2 segundos.

Vale la pena señalar que la masa de la pelota se ignoró por completo en el proceso de resolución del problema. ◊

Generalidades sobre las aplicaciones que llevan a ecuaciones diferenciales

    Para aplicar métodos matemáticos a un problema físico o de la “vida real”, debemos formular el problema en términos matemáticos; es decir, debemos construir un modelo matemático para el problema. Muchos problemas físicos se refieren a las relaciones entre cantidades cambiantes. Dado que las tasas de cambio están representadas matemáticamente por derivadas, los modelos matemáticos a menudo involucran ecuaciones relacionadas con una función desconocida y una o más de sus derivadas. Tales ecuaciones se denominan ecuaciones diferenciales.

    El modelo matemático para un problema aplicado es casi siempre más simple que la situación real en estudio, ya que generalmente se requieren suposiciones simplificadoras para obtener un problema matemático que pueda ser resuelto.  Por ejemplo, al modelar el movimiento de un objeto que cae, podríamos despreciar la resistencia del aire y la atracción gravitacional de cuerpos celestes que no sean la Tierra, o al modelar el crecimiento de la población, podríamos suponer que la población crece continuamente en lugar de en pasos discretos.

    Un buen modelo matemático tiene dos propiedades importantes:

• Es suficientemente simple para que el problema matemático pueda resolverse.
• Represente la situación real lo suficientemente bien como para que la solución al problema matemático  sea una predicción al resultado del problema real dentro de un grado útil de precisión. Si los resultados predichos por el modelo no está de acuerdo con las observaciones físicas, los supuestos subyacentes del modelo deben ser revisados hasta que se obtenga un acuerdo satisfactorio.

     Ahora daremos ejemplos de modelos matemáticos que involucran ecuaciones diferenciales. Volveremos a estos problemas en los momentos apropiados, a medida que aprendamos cómo resolver los diversos tipos de ecuaciones diferenciales que se pueden presentar en los modelos.

Todos los ejemplos en esta sección tratan con funciones donde la variable independiente representa al tiempo, que denotamos por t. Si y es una función de t, y y′ denota la derivada de y con respecto a t; entonces,

Crecimiento y decrecimiento de una población

    Aunque el número de miembros de una población (personas en un país determinado, bacterias en un cultivo de laboratorio, flores silvestres en un bosque, etc.) en un momento dado t es necesariamente un número entero, modelos que usan ecuaciones diferenciales para describir el crecimiento y la decadencia de las poblaciones generalmente se basan en el supuesto simplificador de que el número de miembros de la población puede considerarse como una función diferenciable P = P(t). En la mayoría de modelos se supone que la ecuación diferencial toma la formadonde a es una función continua de P.

En el modelo maltusiano, se supone que a(P) es una constante, por lo que se convierte en

Este modelo supone que los números de nacimientos y muertes por unidad de tiempo son proporcionales a la población. Las constantes de proporcionalidad son la tasa de natalidad (nacimientos por unidad de tiempo por individuo) y la tasa de mortalidad (muertes por unidad de tiempo por individuo); a es la tasa de natalidad menos la tasa de mortalidad.

Aprendiste en cálculo integral que si c es alguna constante, entoncessatisface a, de tal modo que esta ecuación diferencial tiene infinitas soluciones. Para seleccionar la solución particular del problema específico que estamos considerando, debemos conocer la población Po en un momento inicial, digamos en t = 0. Al establecer t = 0 ense obtiene c = P(0) = Po, entonces la solución aplicable esEsto implica quees decir, la población tiende al infinito si la tasa de natalidad excede la tasa de mortalidad, o tiende a cero si la tasa de mortalidad excede la tasa de natalidad.

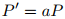
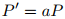
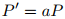
Para ver las limitaciones del modelo maltusiano, supongamos que estamos modelando la población de un país, comenzando desde un tiempo t = 0 cuando la tasa de natalidad excede la tasa de mortalidad (a > 0), y los recursos en términos de espacio, suministro de alimentos y otras necesidades de la vida pueden apoyar a la población existente. En este caso la predicción puede ser razonablemente precisa siempre que permanezca dentro de los límites que los recursos del país pueden soportar. Sin embargo, el modelo inevitablemente debe perder validez cuando la predicción excede estos límites (¡eventualmente no habrá suficiente espacio para la población prevista!).

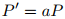
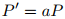
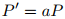
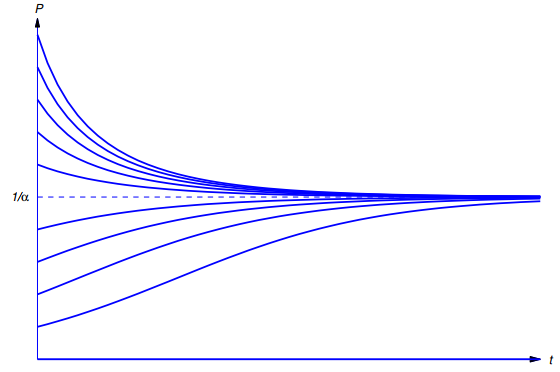
Esta falla en el modelo maltusiano sugiere la necesidad de un modelo que tenga en cuenta las limitaciones de espacio y recursos que tienden a oponerse a la tasa de crecimiento de la población a medida que aumenta la población. Quizás el modelo más famoso de este tipo es el modelo Verhulst, donde se reemplaza por

donde α es una constante positiva. Mientras P sea pequeño en comparación con 1/α, la relación P′/P es aproximadamente igual a a. Por lo tanto, el crecimiento es aproximadamente exponencial; sin embargo, a medida que P aumenta, la relación P′/P disminuye a medida que los factores opuestos se vuelven significativos.

La ecuaciónse conoce como la ecuación logística. La solución de la ecuación logística esdonde Po = P(0) > 0. Por lo tanto, lim_t→∞ P(t) = 1/α, independiente de Po.

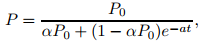
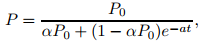
La figura 9.1_5 muestra gráficos típicos de P versus t para varios valores de Po:

La ley de enfriamiento de Newton

Según la ley de enfriamiento de Newton, la temperatura de un cuerpo cambia a un ritmo proporcional a la diferencia entre la temperatura del cuerpo y la temperatura del medio circundante. Por lo tanto, si T_m es la temperatura del medio y T = T(t) es la temperatura del cuerpo en el tiempo t, entoncesdonde k es una constante positiva y el signo menos indica que la temperatura del cuerpo aumenta con el tiempo si es menor que la temperatura del medio, o disminuye si es mayor. Más adelante veremos que si T_m es constante, entonces la solución de la ecuación diferenciales

donde To es la temperatura del cuerpo cuando t = 0. Por lo tanto, lim_t→∞ T(t) = T_m, independiente de T₀.
(El sentido común sugiere esto. ¿Por qué?)

La figura 9.1_6 muestra gráficos típicos de T versus t para varios valores de T₀.

Asumir que el medio permanece a temperatura constante parece razonable si estamos considerando enfriar una taza de café en una habitación, pero no si estamos enfriando un enorme caldero de metal fundido en la misma
habitación. La diferencia entre las dos situaciones es que no es probable que el calor perdido por el café incremente la temperatura de la habitación de manera apreciable, pero sí el calor perdido por el metal que se está enfriando. En esta segunda situación, debemos usar un modelo que explique el calor intercambiado entre el objeto y el medio. Sean T = T(t) y Tm = Tm(t) las temperaturas del objeto y el medio respectivamente, y que T₀ y Tm₀ sean sus valores iniciales. Nuevamente, asumimos que T y Tm están relacionados porTambién suponemos que el cambio en el calor del objeto a medida que su temperatura cambia de T₀ a T es a(T – T₀) y el cambio en el calor del medio a medida que su temperatura cambia de Tm₀ a Tm es am(Tm – Tm₀), donde a y am son constantes positivas dependiendo de las masas y las propiedades térmicas del objeto y el medio, respectivamente. Si suponemos que el calor total del en el objeto y el medio permanece constante (es decir, la energía se conserva), entonces

Resolver esto para Tm y sustituir el resultado enda como resultado la ecuación diferencial

para la temperatura del objeto. Después de aprender a resolver ecuaciones lineales de primer orden, podrás deducir que 

Absorción de glucosa por el cuerpo

    El cuerpo absorbe la glucosa a una velocidad proporcional a la cantidad de glucosa presente en el torrente sanguíneo.
Sea λ la constante (positiva) de proporcionalidad. Supongamos que hay G₀ unidades de glucosa en el torrente sanguíneo cuando t = 0, y sea G = G (t) el número de unidades en el torrente sanguíneo en el tiempo t > 0.
Entonces, dado que la glucosa que absorbe el cuerpo abandona el torrente sanguíneo, G satisface la ecuación

Del cálculo sabes que si c es alguna constante entonces

satisface la ecuación diferencial anterior, y esta función uniparamétrica representa una familia de soluciones, un miembro particular de esta familia para cada valor del parámetro c. Establecer t = 0 en la familia y requerir que G(0) = G₀ produce c = G₀, dedonde, en este caso

    Ahora vamos a complicar las cosas inyectando glucosa por vía intravenosa a una velocidad constante de r unidades de glucosa
por unidad de tiempo. Entonces, la tasa de cambio de la cantidad de glucosa en el torrente sanguíneo por unidad de tiempo es

donde el primer término a la derecha se debe a la absorción de la glucosa por el cuerpo y el segundo término se debe a la inyección. Más adelante estará capacitado podrá mostrar que la solución de la EDque satisface G(0) = G₀ es

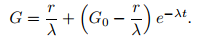
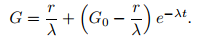
Los gráficos de esta función son similares a los de la figura 9.1_6 (¿Por qué?)

Difusión de epidemias

Un modelo para la propagación de epidemias supone que la cantidad de personas infectadas cambia a un ritmo proporcional al producto de la cantidad de personas ya infectadas y la cantidad de personas que son susceptibles, pero que aún no están infectadas. Por lo tanto, si S denota la población total de personas susceptibles e I = I(t) denota el número de personas infectadas en el momento t, entonces S – I es el número de personas susceptibles, pero aún no infectadas. Así,

donde r es una constante positiva. Suponiendo que I(0) = I₀, la solución de esta ecuación es

Los gráficos de esta función son similares a los de la figura 9.1_5 (¿Por qué?) Dado que lim_{t → ∞} I(t) = S, este modelo predice que todas las personas susceptibles se infectarán.

La segunda ley de movimiento de Newton

    De acuerdo con la segunda ley de movimiento de Newton, la aceleración instantánea a de un objeto con masa constante m está relacionada con la fuerza F que actúa sobre el objeto mediante la ecuación F = ma. Por simplicidad, supongamos que m = 1 y el movimiento del objeto es a lo largo de una recta vertical. Sea y el desplazamiento del objeto desde algún punto de referencia en la superficie de la Tierra, medido positivo hacia arriba. En muchas aplicaciones, hay tres tipos de fuerzas que pueden actuar sobre el objeto:

(a) Una fuerza como la gravedad que depende solo de la posición y, que escribimos como −p(y), donde p(y) > 0 si y ≥ 0.

(b) Una fuerza como la resistencia atmosférica que depende de la posición y la velocidad del objeto, que escribimos como −q(y, y′)y′, donde q es una función no negativa y hemos puesto y′ “afuera” para indicar que la fuerza resistiva siempre está en la dirección opuesta a la velocidad.

(c) Una fuerza f = f (t), ejercida desde una fuente externa (como una línea de remolque desde un helicóptero) que depende solo de t. En este caso, la segunda ley de Newton implica que

que generalmente se reescribe como

Dado que la derivada de segundo orden (y no una superior) de y ocurre en esta ecuación, decimos que es una ecuación diferencial de segundo orden.

Especies que interactúan: Competencia

Supongamos que P = P(t) y Q = Q(t) son las poblaciones de dos especies en el tiempo t, y supongamos que cada población crecería exponencialmente si la otra no existiera; es decir, en ausencia de competencia tendríamos

donde a y b son constantes positivas. Una forma de modelar el efecto de la competencia es asumir que la tasa de crecimiento por individuo de cada población se reduce en una cantidad proporcional a la otra población, entonces las dos ecuaciones anteriores se reemplazan por

donde α y β son constantes positivas. (Dado que la población negativa no tiene sentido, este sistema funciona solo mientras P y Q son positivos.) Ahora suponga que P(0) = P₀ > 0 y Q(0) = Q₀ > 0. Se puede mostrar que hay una constante positiva ρ tal que si (P₀, Q₀) está por encima de la recta L a través del origen con pendiente ρ, entonces la especie con población P se extingue en tiempo finito, pero si (P₀, Q₀) está por debajo de L, la especie con población Q se extingue en tiempo finito. La figura 9.1_7 ilustra esto. Las curvas que se muestran allí están dadas paramétricamente por P = P(t), Q = Q(t), t > 0. Las flechas indican la dirección a lo largo de las curvas con t creciente.