Introducción a las ecuaciones diferenciales

Contenido del capítulo 9.1

• Objetivos de aprendizaje
• Introducción a las ED
• Ecuaciones diferenciales generales
• Definición 9.1.1: Ecuación diferencial
• Definición 9.1.2: Orden de una ecuación diferencial
• Soluciones generales y particulares de una ED
• Problemas de valor inicial (PVI)
• Aplicaciones que llevan a ecuaciones diferenciales
  • Generalidades sobre las aplicaciones que llevan a ED
• Ejercicios resueltos
• Ejercicios propuestos
• Miscelánea de ejercicios

Objetivos de aprendizaje

9.1.1 Identificar el orden de una ecuación diferencial.

9.1.2. Explicar qué se entiende por solución a una ecuación diferencial.

9.1.3. Distinguir entre la solución general y una solución particular de una ecuación diferencial.

9.1.4. Identificar un problema de valor inicial.

9.1.5. Identificar si una función dada es una solución a una ecuación diferencial o a un problema de valor inicial.

Introducción a las ecuaciones diferenciales

    El cálculo es la matemática del cambio, y las tasas de cambio se expresan por derivadas. Por lo tanto, una de las formas más comunes de usar el cálculo es establecer una ecuación que contenga una función desconocida y = f (x) y su(s) derivada(s), conocida como ecuación diferencial. Resolver tales ecuaciones a menudo proporciona información sobre cómo cambian las cantidades y con frecuencia proporciona información sobre cómo y por qué ocurren los cambios.

Las técnicas para resolver ecuaciones diferenciales pueden tomar muchas formas diferentes, incluida la solución directa, el uso de gráficas o los cálculos por computadora. Presentamos las ideas principales en este capítulo y las describimos con un poco más de detalle más adelante en el curso. En esta sección estudiamos qué son las ecuaciones diferenciales, cómo verificar sus soluciones, algunos métodos que se utilizan para resolverlas y algunos ejemplos de ecuaciones comunes y útiles.

Ecuaciones diferenciales generales

Considere la ecuación y′ = 3x², que es un ejemplo de una ecuación diferencial porque incluye una derivada. Existe una relación entre las variables x e y: y es una función desconocida de x. Además, el lado izquierdo de la ecuación es la derivada de y. Por lo tanto, podemos interpretar esta ecuación de la siguiente manera: comience con alguna función y = f (x) y tome su derivada. La respuesta debe ser igual a 3x². ¿Qué función tiene una derivada que sea igual a 3x²? Una de esas funciones es y = x³, por lo que esta función se considera una solución para la ecuación diferencial y′ = 3x².

DEFINICIÓN 9.1.1. Ecuación diferencial

Una ecuación diferencial es una ecuación que involucra una función desconocida y = f (x) y una o más de sus derivadas. Una solución a una ecuación diferencial es una función y = f (x) que satisface la ecuación diferencial cuando f y sus derivadas se sustituyen en la ecuación. ◊

---

Ejemplos de ecuaciones diferenciales y algunos de sus soluciones particulares aparecen en la Tabla 9.1_1.

EJEMPLO ILUSTRATIVO 9.1_1. Verificación de soluciones de ecuaciones diferenciales

Verifique que la función

es una solución a la ecuación diferencial y′ + 3y = 6x + 11.

Solución:

Para verificar la solución, primero calculamos y′ usando la regla de la cadena para derivadas. Esto da

A continuación, sustituimos y e y′ en el lado izquierdo de la ecuación diferencial:

La expresión resultante se puede simplificar distribuyendo primero para eliminar los paréntesis, dando

La combinación de términos similares conduce a la expresión 6x + 11, que es igual al lado derecho de la ecuación diferencial. Este resultado verifica quees una solución de la ecuación diferencial dada.◊

Es conveniente definir características de ecuaciones diferenciales que faciliten hablar sobre ellas y clasificarlas. La característica más básica de una ecuación diferencial es su orden.

DEFINICIÓN 9.1.2.  Orden de una ecuación diferencial

El orden de una ecuación diferencial es el orden más alto de cualquier derivada de la función desconocida que aparece en la ecuación. ◊

EJEMPLO ILUSTRATIVO 9.1_2. Identificando el orden de una ecuación diferencial

¿Cuál es el orden de cada una de las siguientes ecuaciones diferenciales?

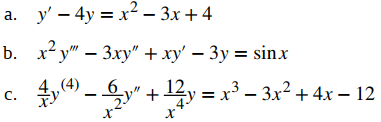
Solución:
a. La derivada más alta en la ecuación es y′, por lo que el orden es 1.
b. La derivada más alta en la ecuación es y″′, por lo que el orden es 3.
c. La derivada más alta en la ecuación es y⁽⁴⁾, por lo que el orden es 4. ◊

Soluciones generales y particulares de una ED

Ya notamos que la ecuación diferencial y′ = 2x tiene al menos dos soluciones: y = x² e y = x² + 4. La única diferencia entre estas dos soluciones es el último término, que es una constante. ¿Qué pasa si el último término es una constante diferente? ¿Esta expresión seguirá siendo una solución a la ecuación diferencial? De hecho, cualquier función de la forma y = x² + C, donde C representa cualquier constante, también es una solución. La razón es que la derivada de x² + C es 2x, independientemente del valor de C. Se puede demostrar que cualquier solución de esta ecuación diferencial debe tener la forma y = x² + C. Este es un ejemplo de una solución general a una ecuación diferencial. En la Figura 9.1_2 se muestra un gráfico de algunas de estas soluciones. (Nota: en este gráfico utilizamos incluso valores enteros para C que oscilan entre −4 y 4. De hecho, no hay restricción en el valor de C; puede ser un entero o no, puede ser cualquier número real).

EJEMPLO ILUSTRATIVO 9.1_3. Encontrar una solución particular

Encuentre la solución particular a la ecuación diferencial y′ = 2x que pasa por el punto (2, 7).

Solución:
Cualquier función de la forma y = x² + C es una solución a esta ecuación diferencial. Para determinar el valor de C, sustituimos los valores x = 2 e y = 7 en esta ecuación y despejamos C:

Por lo tanto, la solución particular que pasa por el punto (2, 7) es y = x² + 3. ◊

pvalorinicial

Problemas de valor inicial (PVI)

Por lo general, una ecuación diferencial dada tiene un número infinito de soluciones, por lo que es natural preguntar cuál queremos usar. Para elegir una solución, se necesita más información. Alguna información específica que puede ser útil es un valor inicial, que es un par ordenado que se utiliza para encontrar una solución particular.

Una ecuación diferencial junto con uno o más valores iniciales se llama un problema de valor inicial. La regla general es que el número de valores iniciales necesarios para un problema de valor inicial es igual al orden de la ecuación diferencial. Por ejemplo, si tenemos la ecuación diferencial y′ = 2x, entonces y(3) = 7 es un valor inicial, y cuando se toman juntas, estas ecuaciones forman un problema de valor inicial. La ecuación diferencial y″ – 3y′ + 2y = 4e× es de segundo orden, por lo que necesitamos dos valores iniciales. Con problemas de valor inicial de orden mayor que uno, se debe usar el mismo valor para la variable independiente. Un ejemplo de valores iniciales para esta ecuación de segundo orden sería y(0) = 2 e y′(0) = – 1. Estos dos valores iniciales junto con la ecuación diferencial forman un problema de valor inicial. Estos problemas se llaman así porque a menudo la variable independiente en la función desconocida es t, que representa el tiempo. Por lo tanto, un valor de t = 0 representa el comienzo del problema.

EJEMPLO ILUSTRATIVO 9.1_4. Verificación de una solución a un problema de valor inicial

Verifique que la función y = 2e⁻²ᵗ + eᵗ es una solución al problema de valor inicial

Solución:
Para que una función satisfaga un problema de valor inicial, debe satisfacer tanto la ecuación diferencial como la condición inicial. Para mostrar que y satisface la ecuación diferencial, comenzamos calculando y′. Esto da y′ = – 4e⁻²ᵗ + eᵗ. A continuación, sustituimos y e y′ en el lado izquierdo de la ecuación diferencial y simplificamos:

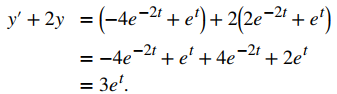
Esto es igual al lado derecho de la ecuación diferencial, por lo que y = 2e⁻²ᵗ + eᵗ resuelve la ecuación diferencial. A continuación calculamos y(0):

Este resultado verifica el valor inicial. Por lo tanto, la función dada satisface el problema de valor inicial.

En el ejemplo 9.1_4, el problema del valor inicial constaba de dos partes. La primera parte fue la ecuación diferencial y′ + 2y = 3eᵗ, y la segunda parte fue el valor inicial y(0) = 3. Estas dos ecuaciones juntas formaron el problema del valor inicial.

Lo mismo es cierto en general. Un problema de valor inicial constará de dos partes: la ecuación diferencial y la condición inicial. La ecuación diferencial tiene una familia de soluciones, y la condición inicial determina el valor de C. La familia de soluciones a la ecuación diferencial en el Ejemplo 9.1_4 viene dada por y = 2e⁻²ᵗ + eᵗ. Esta familia de soluciones se muestra en la Figura 9.1_3, con la solución particular y = 2e⁻²ᵗ + eᵗ etiquetada.

EJEMPLO ILUSTRATIVO 9.1_5. Resolviendo un problema de valor inicial

Resuelva el siguiente problema de valor inicial:

Solución:
El primer paso para resolver este problema de valor inicial es encontrar una familia general de soluciones. Para hacer esto, encontramos una antiderivada de ambos lados de la ecuación diferencial

esto es,

Podemos integrar ambos lados porque el término y aparece solo. Observe que hay dos constantes de integración: C₁ y C₂. Resolviendo la ecuación anterior para y se obtiene

Como C₁ y C₂ son constantes, C₂ − C₁ también es una constante. Por lo tanto, podemos definir C = C₂ − C₁, lo que lleva a la ecuación

Luego determinamos el valor de C. Para hacer esto, sustituimos x = 0 e y = 5 en la ecuación anterior y resolvemos C:

Ahora sustituimos el valor C = 2 en 

La solución al problema del valor inicial es 

Análisis
La diferencia entre una solución general y una solución particular es que una solución general involucra una familia de funciones, definidas explícita o implícitamente, de la variable independiente. El valor o valores iniciales determinan qué solución particular en la familia de soluciones satisface las condiciones deseadas.◊

---

Aplicaciones