| 1. Funciones y sus gráficas | 1.4 Funciones inversas |

Funciones trigonométricas inversas

Las seis funciones trigonométricas básicas son periódicas y, por lo tanto, no son uno a uno. Sin embargo, si restringimos el dominio de una función trigonométrica a un intervalo en el que es uno a uno, podemos definir su inversa. Considere, por ejemplo, la gráfica de la función seno,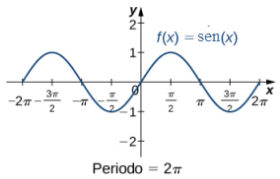 La función seno es uno a uno en un número infinito de intervalos, pero la convención estándar es restringir el dominio al intervalo [−π/2, π/2]. Al hacerlo, definimos la función seno inversa en el dominio [−1, 1] de modo que para cualquier x en el intervalo [−1, 1], la función seno inversa nos dice qué ángulo θ en el intervalo [−π/2, π/2] satisface senθ = x. Del mismo modo, podemos restringir los dominios de las otras funciones trigonométricas para definir funciones trigonométricas inversas, que son funciones que nos dicen qué ángulo en un determinado intervalo tiene un valor trigonométrico específico.

DEFINICIÓN 1.4.3 Inversas de las funciones trigonométricas

•  La función seno inversa, denotada sen⁻¹ o arcsen, y la función coseno inversa, denotada cos⁻¹ o arccos, se definen en el dominio D = {x| −1 ≤ x ≤ 1} de la siguiente manera: sen⁻¹(x) = y  si y sólo si  sen(y) = x  y  − π/2≤ y ≤ π/2; cos⁻¹(x) = y  si y sólo si  cos(y) = x  y  0 ≤ y ≤ π. •  La función tangente inversa, denotada tan⁻¹ o arctan, y la función cotangente inversa, denotada cot⁻¹ o arccot, se definen en el dominio D = {x| −∞ < x < ∞} de la siguiente manera: tan⁻¹(x) = y  si y sólo si  tan(y) = x  y  −π/2 < y < π/2; cot⁻¹(x) = y  si y sólo si  cot(y) = x  y  0 < y < π. •  La función cosecante inversa, denotada csc⁻¹ o arccsc, y la función secante inversa, denotada sec⁻¹ o arcsec, se definen en el dominio D = {x| |x| ≥ 1} de la siguiente manera: csc⁻¹(x) = y  si y sólo si  csc(y) = x  y  − π/2 ≤ y ≤ π/2, y ≠ 0; sec⁻¹(x) = y  si y sólo si  sec(y) = x  y  0 ≤ y ≤ π, y ≠ π/2.

Para graficar las funciones trigonométricas inversas, utilizamos las gráficas de las funciones trigonométricas restringidas a los dominios definidos anteriormente y reflejamos las gráficas sobre la recta y = x (Figura 1.4_5).

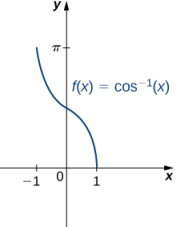
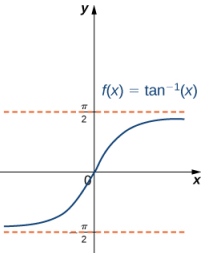
(Figura 1.4_5 La gráfica de cada una de las funciones trigonométricas inversas es una reflexión sobre la recta y = x de la función trigonométrica restringida correspondiente.)

Al evaluar una función trigonométrica inversa, la salida es un ángulo. Por ejemplo, para evaluar cos⁻¹(1/2), necesitamos encontrar un ángulo θ tal que cosθ = 1/2. Claramente, muchos ángulos tienen esta propiedad. Sin embargo, dada la definición de cos⁻¹, necesitamos el ángulo θ que no solo resuelva esta ecuación, sino que también se encuentre en el intervalo [0, π]. Concluimos que cos⁻¹(12) = π/3.

    Ahora consideramos una composición de una función trigonométrica y su inversa. Por ejemplo, considere las dos expresiones sen(sen⁻¹(2/√2)) y sen⁻¹(sen(π)). Para la primera, simplificamos de la siguiente manera:

Para la segunda, tenemos

sen⁻¹ (sen(π)) = sen⁻¹(0) = 0.

Se supone que la función inversa “deshace” la función original, entonces ¿por qué no es sen⁻¹ (sen(π)) = π? Recordando nuestra definición de funciones inversas, una función f y su inversa f⁻¹ satisfacen las condiciones f (f⁻¹(y)) = y para todo y en el dominio de f⁻¹ y f ⁻¹(f (x)) = x para todas las x en el dominio de f, entonces, ¿qué pasó aquí? El problema es que la función seno inversa, sen⁻¹, es la inversa de la función seno restringida definida en el dominio [−π/2, π/2]. Por lo tanto, para x en el intervalo [−π/2, π/2], es cierto que sen⁻¹(senx) = x. Sin embargo, para valores de x fuera de este intervalo, la ecuación no se cumple, aunque sen⁻¹(senx) se define para todos los números reales x.
¿Qué pasa con el sen(sen⁻¹y)? ¿Eso tiene un problema similar? La respuesta es no. Como el dominio de sen⁻¹ es el intervalo [−1, 1], concluimos que sen(sen⁻¹y) = y si −1 ≤ y ≤ 1 y la expresión no está definida para otros valores de y. Para resumir,

sen(sen⁻¹y) = y  si  − 1 ≤ y ≤ 1

y

sen⁻¹(senx) = x  si − π/2 ≤ x ≤ π/2.

Del mismo modo, para la función coseno,

cos(cos⁻¹y) = y  si  −1 ≤ y ≤ 1 

y

cos ⁻¹(cosx) = x  si  0 ≤ x ≤ π.

Propiedades similares se mantienen para las otras funciones trigonométricas y sus inversas.

Ejemplo ilustrativo 1.4_5 Evaluación de expresiones que implican funciones trigonométricas inversas

Evalúa cada una de las siguientes expresiones.

1. Solución:
   Evaluar sen⁻¹(−√3/2) es equivalente a encontrar el ángulo θ tal que senθ = −√3/2 y −π/2 ≤ θ ≤ π/2. El ángulo θ = −π/3 satisface estas dos condiciones. Por lo tanto, sen⁻¹(−√3/2) = – π/3.
2. Primero usamos el hecho de que tan⁻¹(−1/√3) = – π/6. Entonces tan(π/6) =−1/√3. Por lo tanto, tan (tan⁻¹(−1/√3)) =−1/√3.
3. Para evaluar cos⁻¹(cos(5π/4)), primero use el hecho de que cos(5π/4) = –√2/2. Entonces necesitamos encontrar el ángulo θ tal que cos(θ) = –√2/2 y 0 ≤ θ ≤ π. Como 3π/4 satisface ambas condiciones, tenemos que cos(cos⁻¹(5π/4)) = cos(cos⁻¹(–√2/2)) = 3π / 4.
4. Como cos (2π/3) = -1/2, necesitamos evaluar sen◊⁻¹(−1/2). Es decir, necesitamos encontrar el ángulo θ tal que sen (θ) = -1/2 y −π/2 ≤ θ ≤ π/2. Como −π/6 cumple ambas condiciones, podemos concluir que sen⁻¹(cos(2π/3)) = sen⁻¹(−1/2) = – π/6. ◊