| 1. Funciones y sus gráficas | 1.4 Funciones inversas |
Ejercicios propuestos del Capítulo 1.4
Para los siguientes ejercicios, use la prueba de línea horizontal para determinar si cada una de las gráficas dadas es uno a uno.
183.

184.
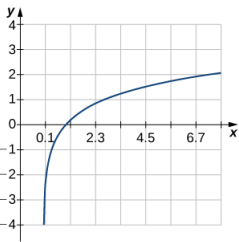
185.
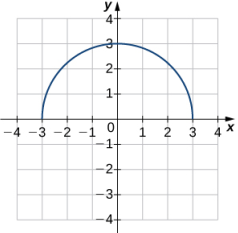
186.

187.

188.

Para los siguientes ejercicios, a. encontrar la función inversa, y b. hallar el dominio y el rango de la función inversa.
Para los siguientes ejercicios, use la gráfica de f para dibujar la gráfica de su función inversa.
195.

196.

197.

198.
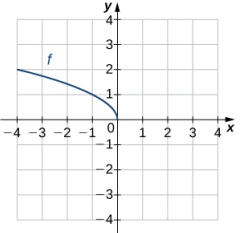
Para los siguientes ejercicios, use la composición para determinar qué pares de funciones son inversas.
199. f (x) = 8x, g(x) = x/8
200. f (x) = 8x + 3, g(x) = (x − 3)/8
201. f (x) = 5x − 7, g(x) = (x + 5)/7
202. f (x) = (2/3)x + 2, g(x) = (3/2)x + 3
203. f (x) = 1/(x − 1), x ≠ 1, g(x) = 1/x + 1, x ≠ 0

205. f (x) = x² + 2x + 1, x ≥ – 1, g(x) = -1 + √x, x ≥ 0
206. f (x) = √(4 − x²), 0 ≤ x ≤ 2, g(x) = √(4 − x²), 0 ≤ x ≤ 2
Para los siguientes ejercicios, evalúe las funciones dadas en el valor especificado. De el valor exacto.
207. tan⁻¹(√3/3)
208. cos⁻¹(−√2/2)
209. cot⁻¹(1)
210. sen⁻¹(−1)
211. cos⁻¹(√3/2)
212. cos(tan⁻¹(√3))
213. sen(cos⁻¹(√2/2))
214. sen⁻¹(sen(π/3))
215. tan⁻¹(tan(−π/6))
216. La función C = T(F) = (5/9)(F − 32) convierte grados Fahrenheit a grados Celsius.
- Encuentre la función inversa F = T ⁻¹(C)
- ¿Para qué se utiliza la función inversa?
217. [T] La velocidad V (en centímetros por segundo) de la sangre en una arteria a una distancia x cm del centro de la arteria se puede modelar mediante la función V = f (x) = 500(0.04 − x²) para 0 ≤ x ≤ 0.2.
- Encuentre x = f ⁻¹(V).
- Interpreta para qué se utiliza la función inversa.
- Encuentre la distancia desde el centro de una arteria con una velocidad de 15 cm/seg, 10 cm/seg y 5 cm/seg. Ver la solución
218. D(x) = 2x + 24 proporciona una función que convierte las tallas de ropa en los Estados Unidos a las de Europa.
- Encuentra las tallas de ropa europeas que corresponden a las tallas 6, 8, 10 y 12 en los Estados Unidos.
- Encuentra la función que convierte las tallas de ropa europeas en tallas de ropa de EE. UU.
- Use la parte b. para encontrar los tamaños de vestido en los Estados Unidos que corresponden a 46, 52, 62 y 70. Ver la solución
219. [T] El costo de eliminar una toxina de un lago está modelado por la función
C(p) = 75p/ (85 − p), donde C es el costo (en miles de dólares) y p es la cantidad de toxina en un pequeño lago (medido en partes por billón [ppb]). Este modelo es válido solo cuando la cantidad de toxina es inferior a 85 ppb.
- Encuentre el costo para eliminar 25 ppb, 40 ppb y 50 ppb de la toxina del lago.
- Encuentra la función inversa.
- Use la parte b. para determinar qué cantidad de toxina se elimina por $ 50,000. Ver la solución
220. [T] Un auto de carreras está acelerando a una velocidad dada por
v(t) = (25/4) t + 54, donde v es la velocidad (en pies por segundo) en el tiempo t.
- Encuentra la velocidad del automóvil a los 10 segundos.
- Encuentra la función inversa.
- Use la parte b. para determinar cuánto tiempo tarda el automóvil en alcanzar una velocidad de 150 pies/seg.
221. [T] El número de Mach M de un avión es la relación entre su velocidad y la velocidad del sonido. Cuando un avión vuela a una altitud constante, entonces su ángulo de Mach viene dado por μ = 2sen⁻¹(1/M).
Encuentre el ángulo de Mach (al grado más cercano) para los siguientes números de Mach.
- M = 1.4
- M = 2.8
- M = 4.3

222. [T] Usando μ = 2sen⁻¹(1/M), encuentre el número de Mach M para los siguientes ángulos.
- μ = π/6
- μ = 2π/7
- μ = 3π/8
223. [T] La siguiente función puede modelar la temperatura promedio (en grados Celsius) de una ciudad en el norte de los Estados Unidos
T(x) = 5 + 18sen [(π/6) (x – 4.6)],
donde x es el tiempo en meses y x = 1.00 corresponde al 1 de enero. Determine el mes y el día en que la temperatura promedio es de 21°C.
224. [T] La profundidad (en pies) del agua en un muelle cambia con el aumento y la caída de las mareas. Está modelado por la función
D(t) = 5se ((π/6)t − 7π/6) + 8, donde t es el número de horas después de la medianoche. Determine la primera vez después de la medianoche cuando la profundidad es de 11.75 pies.
225. [T] Un objeto que se mueve en movimiento armónico simple es modelado por la función
s(t) = – 6cos (πt/2),
donde s se mide en pulgadas y t se mide en segundos. Determine la primera vez cuando la distancia recorrida es de 4.5 pulg.
226. [T] Una galería de arte local tiene un retrato de 3 pies de altura que se cuelga 2.5 pies por encima del nivel de los ojos de una persona promedio. El ángulo de visión θ puede ser modelado por la función
θ = tan⁻¹(5.5)/x − tan⁻¹(2.5)/x,
donde x es la distancia (en pies) del retrato. Encuentre el ángulo de visión cuando una persona está a 4 pies del retrato.
227. [T] Usa una calculadora para evaluar tan⁻¹(tan (2.1)) y cos⁻¹(cos (2.1)). Explica los resultados de cada uno.
228. [T] Usa una calculadora para evaluar sen(sin⁻¹(−2)) y tan(tan⁻¹(−2)). Explica los resultados de cada uno.
