| 2. Límites y continuidad | 2.2 El límite de una función |
Ejercicios propuestos del Capítulo 2.2
Para los siguientes ejercicios, considere la función

30. [T] Complete la siguiente tabla para la función. Redondea tus soluciones a cuatro decimales.
| x | f (x) | x | f (x) |
| 0.9 | a. | 1.1 | e. |
| 0.99 | b. | 1.01 | f. |
| 0.999 | c. | 1.001 | g. |
| 0.9999 | d. | 1.0001 | h. |
31. ¿Qué indican los resultados en el ejercicio anterior sobre el límx→ 1 f (x) al observar los límites unilaterales? Explica tu respuesta.
Para los siguientes ejercicios, considere la función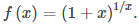
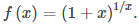
32. [T] Haga una tabla que muestre los valores de f para x = −0.01, −0.001, −0.0001, −0.00001 y para x = 0.01, 0.001, 0.0001, 0.00001. Redondea tus soluciones a cinco cifras decimales.
| x | f (x) | x | f (x) |
| −0.01 | a. | 0.01 | e. |
| −0.001 | b. | 0.001 | f. |
| −0.0001 | c. | 0.0001 | g. |
| −0.00001 | d. | 0.00001 | h. |
33. ¿Qué indica la tabla de valores en el ejercicio anterior acerca de la función

34. ¿A qué constante matemática parece acercarse el límite en el ejercicio anterior?
En los siguientes ejercicios, use los valores dados para configurar una tabla para estimar los límites. Redondea tus soluciones a ocho decimales.
35. [T] limx → 0 sen2x/x; ± 0.1, ± 0.01, ± 0.001, ± .0001
| x | sen2x/x | x | sen2x/x |
|---|---|---|---|
| −0.1 | a. | 0.1 | e. |
| −0.01 | b. | 0.01 | f. |
| −0.001 | c. | 0.001 | g. |
| −0.0001 | d. | 0.0001 | h. |
36. [T] limx → 0 sen3x/x; ± 0.1, ± 0.01, ± 0.001, ± 0.0001
| x | sen3x/x | x | sen3x/x |
|---|---|---|---|
| −0.1 | a. | 0.1 | e. |
| −0.01 | b. | 0.01 | f. |
| −0.001 | c. | 0.001 | g. |
| −0.0001 | d. | 0.0001 | h. |
37. Use los dos ejercicios anteriores para conjeturar (adivinar) el valor del siguiente límite: limx → 0 senax/x para a, un valor real positivo.
[T] En los siguientes ejercicios, configure una tabla de valores para encontrar el límite indicado. Redondea a ocho dígitos.
38. limx → 2 (x² − 4)/(x² + x − 6)
| x | (x² − 4)/(x² + x − 6) | x | (x² − 4)/(x² + x − 6) |
|---|---|---|---|
| 1.9 | a. | 2.1 | e. |
| 1.99 | b. | 2.01 | f. |
| 1.999 | c. | 2.001 | g. |
| 1.9999 | d. |
39. limx → 1 (1 − 2x)
| x | 1 − 2x | x | 1 − 2x |
|---|---|---|---|
| 0.9 | a. | 1.1 | e. |
| 0.99 | b. | 1.01 | f. |
| 0.999 | c. | 1.001 | g. |
| 0.9999 | d. | 1.0001 | h. |
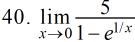
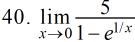
| x |    |
x |    |
|---|---|---|---|
| −0.1 | a. | 0.1 | e. |
| −0.01 | b. | 0.01 | f. |
| −0.001 | c. | 0.001 | g. |
| −0.0001 | d. | 0.0001 | h. |
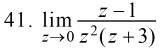
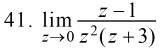
| z | 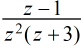 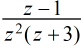 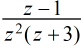 |
z | 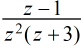 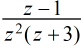 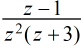 |
|---|---|---|---|
| −0.1 | a. | 0.1 | e. |
| −0.01 | b. | 0.01 | f. |
| −0.001 | c. | 0.001 | g. |
| −0.0001 | d. | 0.0001 | h. |


| t | cost / t |
|---|---|
| 0.1 | a. |
| 0.01 | b. |
| 0.001 | c. |
| 0.0001 | d. |
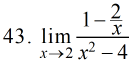
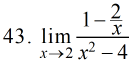
| x | 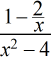 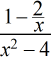 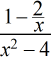 |
x | 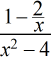 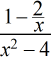 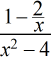 |
|---|---|---|---|
| 1.9 | a. | 2.1 | e. |
| 1.99 | b. | 2.01 | f. |
| 1.999 | c. | 2.001 | g. |
| 1.9999 | d. | 2.0001 | h. |
[T] En los siguientes ejercicios, configure una tabla de valores y redondee a ocho dígitos significativos. Según la tabla de valores, adivine cuál es el límite. Luego, use una calculadora para graficar la función y determinar el límite. ¿Fue correcta la conjetura? Si no, ¿por qué falla el método de tablas?


| θ | 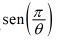 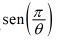 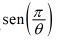 |
θ | 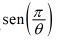 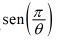 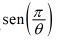 |
|---|---|---|---|
| −0.1 | a. | 0.1 | e. |
| −0.01 | b. | 0.01 | f. |
| −0.001 | c. | 0.001 | g. |
| −0.0001 | d. | 0.0001 | h. |


| a | 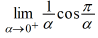 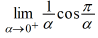 |
|---|---|
| 0.1 | a. |
| 0.01 | b. |
| 0.001 | c. |
| 0.0001 | d. |
En los siguientes ejercicios, considere la gráfica de la función y = f (x) que se muestra aquí. ¿Cuáles de las afirmaciones sobre y = f (x) son verdaderas y cuáles son falsas? Explica por qué una declaración es falsa.
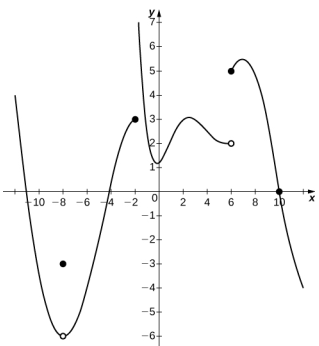
46. limx → 10 f (x) = 0
47. limx → −2⁺ f (x) = 3
48. limx → −8 f (x) = f (−8)
49. limx → 6 f (x) = 5
En los siguientes ejercicios, use la siguiente gráfica de la función y = f (x) para encontrar los valores, si es posible. Estimar cuando sea necesario.
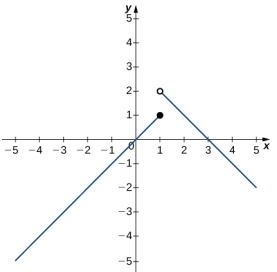

50. limx → 1⁻ f (x)
51. limx → 1⁺ f (x)
52. limx → 1 f (x)
53. limx → 2 f (x)
54. f (1)
En los siguientes ejercicios, use la gráfica de la función y = f (x) que se muestra aquí para encontrar los valores, si es posible. Estimar cuando sea necesario.


55. limx → 0⁻ f (x)
56. limx → 0⁺ f (x)
57. limx → 0 f (x)
58. limx → 2 f (x)
En los siguientes ejercicios, use la gráfica de la función y = f (x) que se muestra aquí para encontrar los valores, si es posible. Estimar cuando sea necesario.


59. limx → −2⁻ f (x)
60. limx → −2⁺ f (x)
61. limx → −2 f (x)
62. limx → 2⁻ f (x)
63. limx → 2⁺ f (x)
64. limx → 2 f (x)
En los siguientes ejercicios, use la gráfica de la función y = g(x) que se muestra aquí para encontrar los valores, si es posible. Estimar cuando sea necesario.


65. limx → 0⁻ g(x)
66. limx → 0⁺ g(x)
67. limx → 0 g(x)
En los siguientes ejercicios, use la gráfica de la función y = h(x) que se muestra aquí para encontrar los valores, si es posible. Estimar cuando sea necesario.
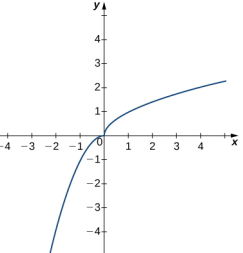

68. limx → 0⁻ h(x)
69. limx → 0⁺ h(x)
70. limx → 0 h(x)
En los siguientes ejercicios, use la gráfica de la función y = f (x) que se muestra aquí para encontrar los valores, si es posible. Estimar cuando sea necesario.


71. limx → 0⁻ f (x)
72. limx → 0⁺ f (x)
73. limx → 0 f (x)
74. limx → 1 f (x)
75. limx → 2 f (x)

Enhorabuena! y muchas gracias por su blog, lo descubrí de manera casual y he encontrado una exposición clara concisa y concreta, de verdad que parece que la pantalla habla por sí sola. Un saludo!!
¡Gracias por tu maravillosa publicación! Realmente disfruté leyéndolo, podrías ser un gran autor. Siempre marcaré su blog y, a menudo, volveré por aquí. ¡Quiero animarlos a continuar con su gran trabajo, que tengan una buena noche!