(Límites y continuidad)
Límites infinitos
Evaluar el límite de una función en un punto o evaluar el límite de una función desde la derecha y la izquierda en un punto nos ayuda a caracterizar el comportamiento de una función en torno a un valor dado. Como veremos, también podemos describir el comportamiento de funciones que no tienen límites finitos.
Ahora dirigimos nuestra atención a h(x) = 1/(x − 2)², la tercera y última función introducida al comienzo de esta sección (ver Figura 2.2_1 (c)).
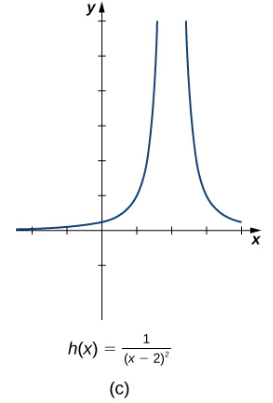
De su gráfica vemos que a medida que los valores de x se aproximan a 2, los valores de h(x) = 1/(x − 2)² se hacen cada vez más grandes y, de hecho, se vuelven infinitos. Matemáticamente, decimos que el límite de h(x) cuando x se acerca a 2 es infinito positivo. Simbólicamente, expresamos esta idea como
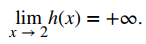
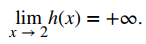
De manera más general, definimos límites infinitos de la siguiente manera:
DEFINICIÓN . Límites infinitos
|
Definimos tres tipos de límites infinitos. Límites infinitos desde la izquierda: Sea f (x) una función definida en todos los valores en un intervalo abierto de la forma (b, a). i. Si los valores de f (x) aumentan sin límite a medida que los valores de x (donde x < a) se acercan al número a, entonces decimos que el límite a medida que x se aproxima a a desde la izquierda es infinito positivo y escribimos ii. Si los valores de f (x) disminuyen sin límite a medida que los valores de x (donde x < a) se acercan al número a, entonces decimos que el límite a medida que x se acerca a a desde la izquierda es infinito negativo y escribimos Límites infinitos desde la derecha: Sea f (x) una función definida en todos los valores en un intervalo abierto de la forma (a, c). ii. Si los valores de f (x) disminuyen sin límite a medida que los valores de x (donde x > a) se acercan al número a, entonces decimos que el límite a medida que x se acerca a a desde la derecha es infinito negativo y escribimos Límite infinito desde los dos lados (bilateral): deje que f (x) se defina para todo x ≠ a en un intervalo abierto que contenga a a. i. Si los valores de f (x) aumentan sin límite a medida que los valores de x (donde x ≠ a) se acercan al número a, entonces decimos que el límite a medida que x se acerca a a es infinito positivo y escribimos ii. Si los valores de f (x) disminuyen sin límite a medida que los valores de x (donde x ≠ a) se acercan al número a, entonces decimos que el límite a medida que x se acerca a a es infinito negativo y escribimos |
Es importante comprender que cuando escribimos enunciados como limx → a f (x) = + ∞ o limx → a f (x) = – ∞ estamos describiendo el comportamiento de la función, tal como la acabamos de definir. No estamos afirmando que existe un límite. Para que el límite de una función f (x) exista en a, debe aproximarse a un número real L a medida que x se aproxima a a tanto por la izquierda como por la derecha.
Ejemplo ilustrativo 2.2_6 Reconociendo un límite infinito
Evalúe cada uno de los siguientes límites, si es posible. Use una tabla de valores funcionales y un gráfico f (x) = 1/x para confirmar su conclusión.


Solución:
Comience por construir una tabla de valores funcionales.


a. Los valores de 1/ x disminuyen sin límite cuando x se acerca a 0 desde la izquierda. Concluimos que
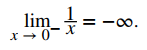
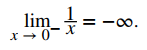
b. Los valores de 1/x aumentan sin límite cuando x se acerca a 0 desde la derecha. Concluimos que
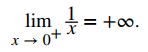
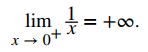
c. Como limx → 0− 1/x = −∞ y limx → 0+ 1/x = +∞ tienen valores (tendencias) diferentes, concluimos que


La gráfica de f (x) = 1/x en la figura 2.2_7 confirma estas conclusiones.
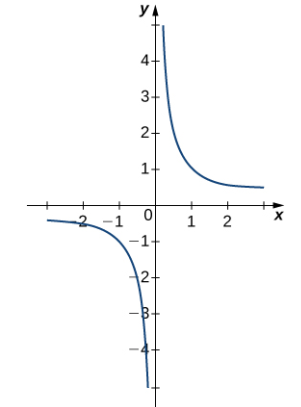

Ejercicio de control 2.2_5
Evalúe cada uno de los siguientes límites, si es posible. Use una tabla de valores funcionales y una gráfica f (x) = 1 / x² para confirmar su conclusión.
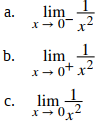
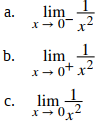
Es útil señalar que las funciones de la forma f (x) = 1/(x − a)ⁿ, donde n es un número entero positivo, tienen límites infinitos a medida que x se acerca a a desde la izquierda o la derecha (Figura 2.2_8). Estos límites se resumen en Límites infinitos de enteros positivos.


TEOREMA 2.2.3 Límites infinitos de enteros positivos
|
Si n es un entero par positivo, entonces
Si n es un entero impar positivo, entonces
y
|
También debemos señalar que en las gráficas de f (x) = 1 / (x − a)ⁿ, los puntos en la gráfica que tienen coordenadas x muy cerca de a están muy cerca de la recta vertical x = a. Es decir, a medida que x se acerca a a, los puntos en la gráfica de f (x) están más cerca de la recta x = a. La recta x = a se llama asíntota vertical de la gráfica. Definimos formalmente una asíntota vertical de la siguiente manera:
DEFINICIÓN. Asíntota vertical
|
Sea f (x) una función. Si se cumple alguna de las siguientes condiciones, entonces la recta x = a es una asíntota vertical de f (x).
|
Ejemplo ilustrativo 2.2_7 Encontrar una asíntota vertical
Evalúe cada uno de los siguientes límites utilizando límites infinitos de enteros positivos. Identifique las asíntotas verticales de la función f (x) = 1 / (x + 3)⁴.
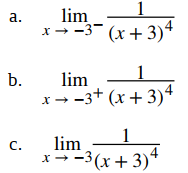
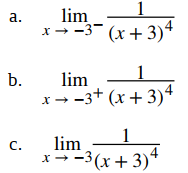
Solución:
Podemos usar límites infinitos de enteros positivos directamente (Teorema 2.2_3).


La función f (x) = 1 / (x + 3)⁴ tiene una asíntota vertical de x = −3.
Ejercicio de control 2.2_6
Evalúe cada uno de los siguientes límites. Identifique las asíntotas verticales de la función f (x) = 1 / (x − 2)³.
En el siguiente ejemplo, utilizamos nuestro conocimiento de varios tipos de límites para analizar el comportamiento de una función en varios puntos diferentes.
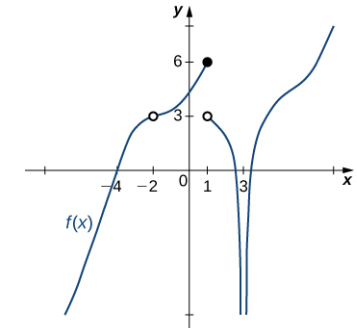
Ejemplo ilustrativo 2.2_8 Comportamiento de una función en diferentes puntos
Use la gráfica de f (x) en la Figura 2.2._9 para determinar cada uno de los siguientes valores:
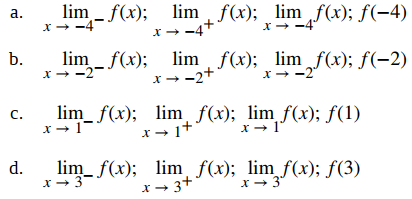

Solución:
Usando límites infinitos de enteros positivos y la gráfica como referencia, llegamos a los siguientes valores:
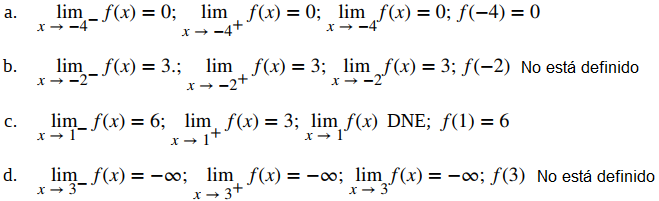
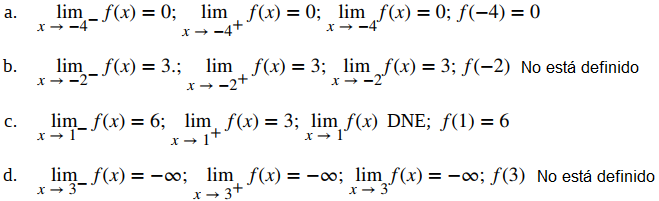
Ejercicio de control 2.2_7
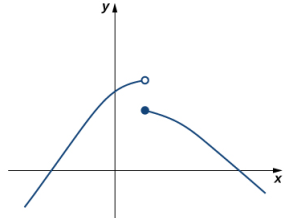
Evalúe limx → 1f (x) para f (x) cuya gráfica se muestra aquí:

Ejemplo ilustrativo 2.2_9 La ecuación de Einstein


En el primer capítulo mencionamos brevemente cómo Albert Einstein demostró que existe un límite para la velocidad con la que puede viajar cualquier objeto. Dada la ecuación de Einstein para la masa de un objeto en movimiento, ¿cuál es el valor de este límite?
Solución:
Nuestro punto de partida es la ecuación de Einstein para la masa de un objeto en movimiento,


donde m0 es la masa del objeto en reposo, v es su velocidad y c es la velocidad de la luz. Para ver cómo cambia la masa a altas velocidades, podemos graficar la relación de masas m / m0 en función de la relación de velocidades, v / c (Figura 2.2.11).
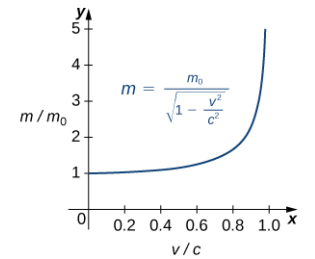

Figura 2.2.11 Esta gráfica muestra la relación de masas en función de la relación de velocidades en la ecuación de Einstein para la masa de un objeto en movimiento.
Podemos ver que a medida que la relación de velocidades se aproxima a 1, es decir, a medida que la velocidad del objeto se acerca a la velocidad de la luz, la relación de masas aumenta sin límite. En otras palabras, la función tiene una asíntota vertical en v / c = 1. Podemos probar algunos valores de esta relación para probar esta idea.
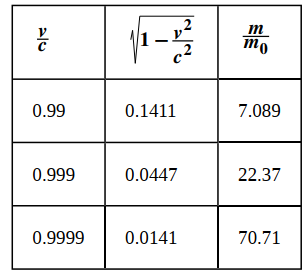

Tabla 2.2.8 Relación de masas y velocidades para un objeto en movimiento
Por lo tanto, de acuerdo con la Tabla 2.2.8, si un objeto con una masa de 100 kg viaja a 0.9999c, su masa se convierte en 7071 kg. Dado que ningún objeto puede tener una masa infinita, concluimos que ningún objeto puede viajar a la velocidad de la luz o más.

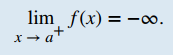
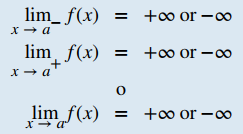
Enhorabuena! y muchas gracias por su blog, lo descubrí de manera casual y he encontrado una exposición clara concisa y concreta, de verdad que parece que la pantalla habla por sí sola. Un saludo!!
¡Gracias por tu maravillosa publicación! Realmente disfruté leyéndolo, podrías ser un gran autor. Siempre marcaré su blog y, a menudo, volveré por aquí. ¡Quiero animarlos a continuar con su gran trabajo, que tengan una buena noche!