Aplicaciones físicas de la integral

Trabajo realizado por una fuerza

Ahora consideramos el trabajo. En física, el trabajo está relacionado con la fuerza, que a menudo se define intuitivamente como empujar o tirar de un objeto. Cuando una fuerza mueve un objeto, decimos que la fuerza funciona sobre el objeto. En otras palabras, el trabajo puede considerarse como la cantidad de energía que se necesita para mover un objeto. Según la física, cuando tenemos una fuerza constante, el trabajo puede expresarse como el producto de la fuerza y la distancia.

En el sistema inglés, la unidad de fuerza es la libra y la unidad de distancia es el pie, por lo que el trabajo se da en pie-libras. En el sistema métrico, se utilizan kilogramos y metros. Un newton es la fuerza necesaria para acelerar 1 kilogramo de masa a una velocidad de 1 m / seg2. Por lo tanto, la unidad de trabajo más común es el newton-metro. Esta misma unidad también se llama joule. Ambos se definen como kilogramos por metros al cuadrado sobre segundos al cuadrado (kg⋅m2/s2).

Cuando tenemos una fuerza constante, las cosas son bastante fáciles. Sin embargo, es raro que una fuerza sea constante. El trabajo realizado para comprimir (o alargar) un resorte, por ejemplo, varía dependiendo de cuánto se haya comprimido (o estirado) el resorte. Estudiaremos los resortes con más detalle más adelante en esta sección.

Supongamos que tenemos una fuerza variable F(x) que mueve un objeto en una dirección positiva a lo largo del eje x desde el punto a hasta el punto b. Para calcular el trabajo realizado, dividimos el intervalo [a, b] y estimamos el trabajo realizado sobre cada subintervalo. Entonces, para i = 0, 1, 2, …, n, dejemos que P = {x_i} sea una partición regular del intervalo [a, b], y para i = 1, 2, …, n, elija un punto arbitrario x_i* ∈ [x_{i − 1}, x_i]. Para calcular el trabajo realizado para mover un objeto desde el punto x_{i − 1} al punto x_i, suponemos que la fuerza es aproximadamente constante durante el intervalo, y usamos F(x_i*) para aproximar la fuerza. El trabajo realizado durante el intervalo [x_{i − 1}, x_i], entonces, viene dado por

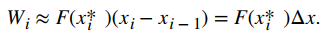
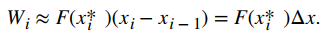
Por lo tanto, el trabajo realizado durante el intervalo [a, b] es aproximadamente

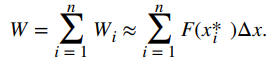
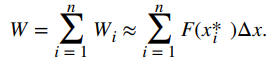
Tomar el límite de esta expresión cuando n → ∞ nos da el valor exacto para el trabajo:

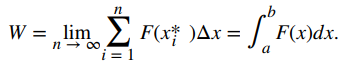
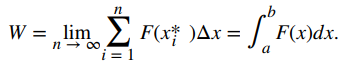
Por lo tanto, podemos definir el trabajo de la siguiente manera.

Definición 6.5.1. Trabajo

Si una fuerza variable F(x) mueve un objeto en una dirección positiva a lo largo del eje x desde el punto a hasta el punto b, entonces el trabajo realizado sobre el objeto es

---

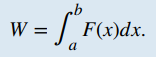
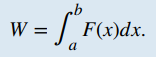
Tenga en cuenta que si F es constante, la integral se evalúa como F⋅ (b − a) = F⋅ d, que es la fórmula que establecimos al comienzo de esta sección.

Ahora veamos el ejemplo específico del trabajo realizado para comprimir o alargar un resorte. Considere un bloque unido a un resorte horizontal. El bloque se mueve hacia adelante y hacia atrás a medida que el resorte se estira y comprime. Aunque en el mundo real tendríamos que tener en cuenta la fuerza de fricción entre el bloque y la superficie sobre la que descansa, ignoramos la fricción aquí y asumimos que el bloque descansa sobre una superficie sin fricción. Cuando el resorte está en su longitud natural (en reposo), se dice que el sistema está en equilibrio. En este estado, el resorte no es ni alargado ni comprimido, y en esta posición de equilibrio, el bloque no se mueve hasta que se introduce alguna fuerza. Orientamos el sistema de modo que x = 0 corresponda a la posición de equilibrio (vea la siguiente figura).

Según la ley de Hooke, la fuerza requerida para comprimir o estirar un resorte desde una posición de equilibrio viene dada por F(x) = kx, para alguna constante k. El valor de k depende de las características físicas del resorte. La constante k se llama constante del resorte y siempre es positiva. Podemos usar esta información para calcular el trabajo realizado para comprimir o alargar un resorte, como se muestra en los videos sobre los Ejercicios resueltos.

Ejercicios resueltos