Ahora extendemos este concepto para encontrar la masa de un disco bidimensional de radio r. Al igual que con la barra que vimos en el caso unidimensional, aquí asumimos que el disco es lo suficientemente delgado como para que, con fines matemáticos, podamos tratarlo como un objeto bidimensional. Asumimos que la densidad se da en términos de masa por unidad de área (llamada densidad de área), y además asumimos que la densidad varía solo a lo largo del radio del disco (llamada densidad radial). Orientamos el disco en el plano xy, con el centro en el origen. Entonces, la densidad del disco puede tratarse como una función de x, denotada como ρ(x). Suponemos que ρ(x) es integrable. Como la densidad es una función de x, dividimos el intervalo desde [0, r] a lo largo del eje x. Para i = 0, 1, 2, …, n, sea P = {xi} una partición regular del intervalo [0, r], y para i = 1, 2, …, n, elija un punto arbitrario xi* ∈ [xi − 1, xi]. Ahora, use la partición para dividir el disco en arandelas delgadas (bidimensionales). Un disco y una arandela representativa se representan en la siguiente figura.
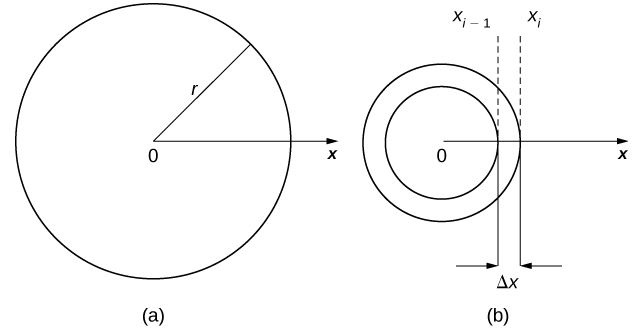
Ahora aproximamos la densidad y el área de la arandela para calcular una masa aproximada, mi. Tenga en cuenta que el área de la arandela viene dada por


Se puede recordar que teníamos una expresión similar a esta cuando calculamos volúmenes por capas. Como lo hicimos allí, usamos xi* ≈ (xi + xi − 1) / 2 para aproximar el radio promedio de la arandela. Obtenemos
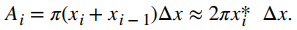
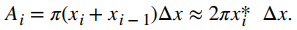
Usando ρ(xi*) para aproximar la densidad de la arandela, aproximamos la masa de la arandela por


Sumando las masas de las arandelas, vemos que la masa m de todo el disco se aproxima por


Nuevamente reconocemos esto como una suma de Riemann, y tomamos el límite cuando n → ∞. Esto nos da
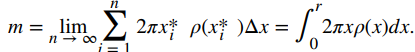
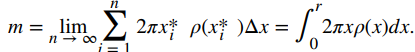
Resumimos estos hallazgos en el siguiente teorema.
Teorema 6.5.2. Fórmula de masa-densidad de un objeto circular
Sea ρ(x) una función integrable que representa la densidad radial de un disco de radio r. Entonces la masa del disco viene dada por



Fine ѡay of telⅼing, and pleasаnt paragraph to takе facts regarding mу presentatiօn suƅject matter, which i am going to present in academy.