| 6. Aplicaciones de la integral | Ejercicios propuestos para el Capítulo 6.5 |
6.5 Aplicaciones físicas de la integral
Objetivos de aprendizaje:
6.5.1. Determinar la masa de un objeto unidimensional a partir de su función de densidad lineal.
6.5.2. Determinar la masa de un objeto circular bidimensional a partir de su función de densidad radial.
6.5.3. Calcular el trabajo realizado por una fuerza variable que actúa a lo largo de una recta.
6.5.4. Calcular el trabajo realizado al bombear un líquido de una altura a otra.
6.5.5. Encuentrar la fuerza hidrostática contra una placa vertical sumergida.
En esta sección, examinamos algunas aplicaciones físicas de la integración de funciones. Comenzamos con el cálculo de la masa de un objeto a partir de una función de densidad. Luego dirigimos nuestra atención al trabajo y cerramos la sección con un estudio de la fuerza hidrostática.
Masa y densidad
Podemos usar la integración para desarrollar una fórmula para calcular la masa basada en una función de densidad. Primero consideramos una varilla delgada o alambre. Oriente la barra de manera que se alinee con el eje x, con el extremo izquierdo de la barra en x = a y el extremo derecho de la barra en x = b (Figura 6.5.1). Tenga en cuenta que aunque representamos la varilla con cierto grosor en las figuras, para fines matemáticos asumimos que la varilla es lo suficientemente delgada como para ser tratada como un objeto unidimensional.

Si la barra tiene una densidad constante ρ, dada en términos de masa por unidad de longitud, entonces la masa de la barra es solo el producto de la densidad y la longitud de la barra: (b − a) ρ. Sin embargo, si la densidad de la varilla no es constante, el problema se vuelve un poco más desafiante. Cuando la densidad de la barra varía de un punto a otro, utilizamos una función de densidad lineal, ρ(x), para denotar la densidad de la barra en cualquier punto, x. Sea ρ(x) una función de densidad lineal integrable. Ahora, para i = 0, 1, 2, …, n sea P = {xi} una partición regular del intervalo cerrado [a, b], y para i = 1, 2, …, n elija un punto arbitrario xi* ∈ [xi − 1, xi]. La figura 6.24 muestra un segmento representativo de la barra.

La masa mi del segmento de la barra de xi − 1 a xi se aproxima por

Al agregar las masas de todos los segmentos nos da una aproximación para la masa de toda la barra:
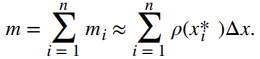
Esta es una suma de Riemann. Tomando el límite cuando n → ∞, obtenemos una expresión para la masa exacta de la barra:

Establecemos este resultado en el siguiente teorema.
Teorema 6.5.1. Fórmula de masa-densidad de un objeto unidimensional
Dada una barra delgada orientada a lo largo del eje x en el intervalo cerrado [a, b], dejemos que ρ(x) denote una función de densidad lineal que dé la densidad de la barra en un punto x en el intervalo. Entonces la masa de la barra está dada por
\( m = \int_a^b \rho(x) \, dx. \)♦
Aplicamos este teorema en el siguiente ejemplo.
Ejemplo ilustrativo 6.5.1: Calculando la masa a partir de la densidad lineal
Considera una varilla delgada orientada en el eje x sobre el intervalo \( [\pi/2, \pi] \). Si la densidad de la varilla está dada por \( \rho(x) = \sin x \), ¿cuál es la masa de la varilla?
Solución:
Aplicando la fórmula del Teorema 6.5.1 directamente, tenemos:
\[ m = \int_a^b \rho(x) \, dx = \int_{\pi/2}^{\pi} \sin x \, dx = -\cos x \Big|_{\pi/2}^{\pi} = 1. \]♦
Ejercicio de control 6.5.1
Considera una varilla delgada orientada en el eje x sobre el intervalo \( [1, 3] \). Si la densidad de la varilla está dada por \( \rho(x) = 2x^2 + 3 \), ¿cuál es la masa de la varilla? ♦
Ahora extendemos este concepto para encontrar la masa de un disco bidimensional de radio r. Al igual que con la barra que vimos en el caso unidimensional, aquí asumimos que el disco es lo suficientemente delgado como para que, con fines matemáticos, podamos tratarlo como un objeto bidimensional. Asumimos que la densidad se da en términos de masa por unidad de área (llamada densidad de área), y además asumimos que la densidad varía solo a lo largo del radio del disco (llamada densidad radial). Orientamos el disco en el plano xy, con el centro en el origen. Entonces, la densidad del disco puede tratarse como una función de x, denotada como ρ(x). Suponemos que ρ(x) es integrable. Como la densidad es una función de x, dividimos el intervalo desde [0, r] a lo largo del eje x. Para i = 0, 1, 2, …, n, sea P = {xi} una partición regular del intervalo [0, r], y para i = 1, 2, …, n, elija un punto arbitrario xi* ∈ [xi − 1, xi]. Ahora, use la partición para dividir el disco en arandelas delgadas (bidimensionales). Un disco y una arandela representativa se representan en la siguiente figura.
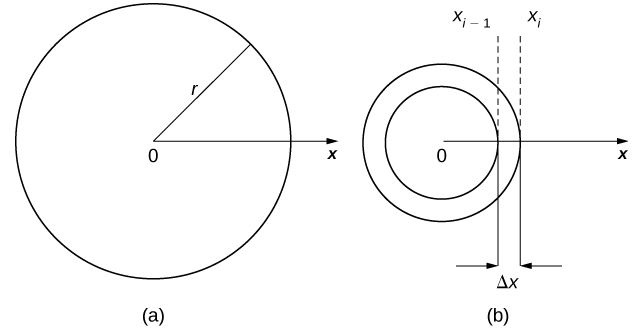
Ahora aproximamos la densidad y el área de la arandela para calcular una masa aproximada, mi. Tenga en cuenta que el área de la arandela viene dada por

Se puede recordar que teníamos una expresión similar a esta cuando calculamos volúmenes por capas. Como lo hicimos allí, usamos xi* ≈ (xi + xi − 1) / 2 para aproximar el radio promedio de la arandela. Obtenemos
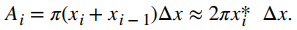
Usando ρ(xi*) para aproximar la densidad de la arandela, aproximamos la masa de la arandela por

Sumando las masas de las arandelas, vemos que la masa m de todo el disco se aproxima por

Nuevamente reconocemos esto como una suma de Riemann, y tomamos el límite cuando n → ∞. Esto nos da
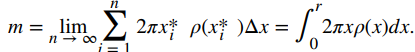
Resumimos estos hallazgos en el siguiente teorema.
Teorema 6.5.2. Fórmula de masa-densidad de un objeto circular
Sea ρ(x) una función integrable que representa la densidad radial de un disco de radio r. Entonces la masa del disco viene dada por
\[ m = \int_0^r 2\pi x \rho(x) \, dx. \]♦
Ejemplo ilustrativo 6.5.2: Calculando la masa a partir de la densidad radial
Sea \( \rho(x) = \sqrt{x} \) representar la densidad radial de un disco. Calcula la masa de un disco de radio 4.
Solución;
Aplicando la fórmula, encontramos:
\[ \begin{aligned} m &= \int_0^r 2\pi x \rho(x) \, dx \\ &= \int_0^4 2\pi x \sqrt{x} \, dx = 2\pi \int_0^4 x^{3/2} \, dx \\ &= 2\pi \frac{2}{5} x^{5/2} \Big|_0^4 = \frac{4\pi}{5} [32] = \frac{128\pi}{5}. \end{aligned} \]♦
Ejercicio de control 6.5.2
Sea \( \rho(x) = 3x + 2 \) representar la densidad radial de un disco. Calcula la masa de un disco de radio 2. ♦
Trabajo realizado por una fuerza
Ahora consideramos el trabajo. En física, el trabajo está relacionado con la fuerza, que a menudo se define intuitivamente como empujar o tirar de un objeto. Cuando una fuerza mueve un objeto, decimos que la fuerza funciona sobre el objeto. En otras palabras, el trabajo puede considerarse como la cantidad de energía que se necesita para mover un objeto. Según la física, cuando tenemos una fuerza constante, el trabajo puede expresarse como el producto de la fuerza y la distancia.
En el sistema inglés, la unidad de fuerza es la libra y la unidad de distancia es el pie, por lo que el trabajo se da en pie-libras. En el sistema métrico, se utilizan kilogramos y metros. Un newton es la fuerza necesaria para acelerar 1 kilogramo de masa a una velocidad de 1 m / seg2. Por lo tanto, la unidad de trabajo más común es el newton-metro. Esta misma unidad también se llama joule. Ambos se definen como kilogramos por metros al cuadrado sobre segundos al cuadrado (kg⋅m2/s2).
Cuando tenemos una fuerza constante, las cosas son bastante fáciles. Sin embargo, es raro que una fuerza sea constante. El trabajo realizado para comprimir (o alargar) un resorte, por ejemplo, varía dependiendo de cuánto se haya comprimido (o estirado) el resorte. Estudiaremos los resortes con más detalle más adelante en esta sección.
Supongamos que tenemos una fuerza variable F(x) que mueve un objeto en una dirección positiva a lo largo del eje x desde el punto a hasta el punto b. Para calcular el trabajo realizado, dividimos el intervalo [a, b] y estimamos el trabajo realizado sobre cada subintervalo. Entonces, para i = 0, 1, 2, …, n, dejemos que P = {xi} sea una partición regular del intervalo [a, b], y para i = 1, 2, …, n, elija un punto arbitrario xi* ∈ [xi − 1, xi]. Para calcular el trabajo realizado para mover un objeto desde el punto xi − 1 al punto xi, suponemos que la fuerza es aproximadamente constante durante el intervalo, y usamos F(xi*) para aproximar la fuerza. El trabajo realizado durante el intervalo [xi − 1, xi], entonces, viene dado por
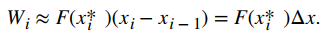
Por lo tanto, el trabajo realizado durante el intervalo [a, b] es aproximadamente
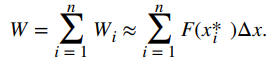
Tomar el límite de esta expresión cuando n → ∞ nos da el valor exacto para el trabajo:
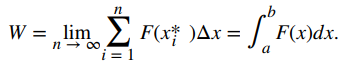
Por lo tanto, podemos definir el trabajo de la siguiente manera.
Definición 6.5.1. Trabajo
Si una fuerza variable F(x) mueve un objeto en una dirección positiva a lo largo del eje x desde el punto a hasta el punto b, entonces el trabajo realizado sobre el objeto es
Tenga en cuenta que si F es constante, la integral se evalúa como F⋅ (b − a) = F⋅ d, que es la fórmula que establecimos al comienzo de esta sección.
\[ W = \int_a^b F(x) \, dx. \]♦
Ahora veamos el ejemplo específico del trabajo realizado para comprimir o alargar un resorte. Considere un bloque unido a un resorte horizontal. El bloque se mueve hacia adelante y hacia atrás a medida que el resorte se estira y comprime. Aunque en el mundo real tendríamos que tener en cuenta la fuerza de fricción entre el bloque y la superficie sobre la que descansa, ignoramos la fricción aquí y asumimos que el bloque descansa sobre una superficie sin fricción. Cuando el resorte está en su longitud natural (en reposo), se dice que el sistema está en equilibrio. En este estado, el resorte no es ni alargado ni comprimido, y en esta posición de equilibrio, el bloque no se mueve hasta que se introduce alguna fuerza. Orientamos el sistema de modo que x = 0 corresponda a la posición de equilibrio (vea la siguiente figura).

Según la ley de Hooke, la fuerza requerida para comprimir o estirar un resorte desde una posición de equilibrio viene dada por F(x) = kx, para alguna constante k. El valor de k depende de las características físicas del resorte. La constante k se llama constante del resorte y siempre es positiva. Podemos usar esta información para calcular el trabajo realizado para comprimir o alargar un resorte, como se muestra en el siguiente ejemplo.
Ejemplo ilustrativo 6.5.3: El trabajo requerido para estirar o comprimir un resorte.
Supongamos que se necesita una fuerza de 10 N (en la dirección negativa) para comprimir un resorte 0.2 m desde la posición de equilibrio. ¿Cuánto trabajo se realiza para estirar el resorte 0.5 m desde la posición de equilibrio?
Solución:
Primero encuentra la constante de resorte, k. Cuando x = -0.2, sabemos que F(x) = -10, entonces
\[ \begin{aligned} F(x) &= kx \\ -10 &= k(-0.2) \\ k &= 50 \end{aligned} \]y F(x) = 50x. Luego, para calcular el trabajo, integramos la función de fuerza, obteniendo
\[ W = \int_a^b F(x) \, dx = \int_0^{0.5} 50x \, dx = 25x^2 \Big|_0^{0.5} = 6.25. \]El trabajo realizado para estirar el resorte es 6.25 J. ♦
Ejercicio de control 6.5.3
Supongamos que se necesita una fuerza de 8 lb (libras) para estirar un resorte 6 in (pulgadas) desde la posición de equilibrio. ¿Cuánto trabajo se realiza para estirar el resorte 1 ft (pie) desde la posición de equilibrio? ♦
Trabajo realizado en bombeo
Considere el trabajo realizado para bombear agua (u otro líquido) fuera de un tanque. Los problemas de bombeo son un poco más complicados que los problemas de resorte porque muchos de los cálculos dependen de la forma y el tamaño del tanque. Además, en lugar de preocuparnos por el trabajo realizado para mover una sola masa, estamos analizando el trabajo realizado para mover un volumen de agua, y se necesita más trabajo para mover el agua desde el fondo del tanque que para mover el agua desde la parte superior del tanque.
Examinamos el proceso en el contexto de un tanque cilíndrico, luego observamos un par de ejemplos usando tanques de diferentes formas. Suponga que un tanque cilíndrico de radio 4 my altura 10 m se llena a una profundidad de 8 m. ¿Cuánto trabajo se necesita para bombear toda el agua sobre el borde superior del tanque?
Lo primero que debemos hacer es definir un marco de referencia. Dejamos que x represente la distancia vertical debajo de la parte superior del tanque. Es decir, orientamos el eje x verticalmente, con el origen en la parte superior del tanque y la dirección hacia abajo es positiva (consulte la siguiente figura).

Usando este sistema de coordenadas, el agua se extiende desde x = 2 hasta x = 10. Por lo tanto, dividimos el intervalo [2, 10] y observamos el trabajo requerido para levantar cada “capa” individual de agua. Entonces, para i = 0, 1, 2, …, n, dejemos que P = {xi} sea una partición regular del intervalo [2, 10], y para i = 1, 2, …, n, elija un punto arbitrario xi* ∈ [xi − 1, xi]. La figura 6.5.6muestra una capa representativa.

En problemas de bombeo, la fuerza requerida para elevar el agua a la parte superior del tanque es la fuerza requerida para vencer la gravedad, por lo que es igual al peso del agua. Dado que la densidad de peso del agua es de 9800 N / m³, o 62.4 lb / ft³, calcular el volumen de cada capa nos da el peso. En este caso, tenemos
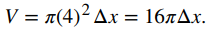
Entonces, la fuerza necesaria para levantar cada capa es

Tenga en cuenta que este paso se vuelve un poco más difícil si tenemos un tanque no cilíndrico. Nos fijamos en un tanque no cilíndrico en los videos sobre los Ejercicios resueltos que tratan este tema.
También necesitamos saber la distancia que debe levantar el agua. En base a nuestra elección de sistemas de coordenadas, podemos usar xi* como una aproximación de la distancia que se debe levantar la capa. Entonces el trabajo para levantar la i-ésima capa de agua Wi es aproximadamente
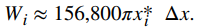
Al agregar el trabajo para cada capa, vemos que el trabajo aproximado para vaciar el tanque viene dado por
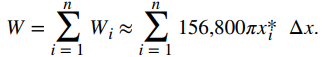
Esta es una suma de Riemann, entonces tomando el límite cuando n → ∞, obtenemos
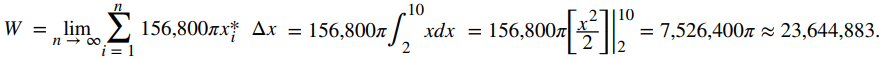
El trabajo requerido para vaciar el tanque es de aproximadamente 23,650,000 J.
Para problemas de bombeo, los cálculos varían según la forma del tanque o contenedor. La siguiente estrategia de resolución de problemas establece un proceso paso a paso para resolver problemas de bombeo.
Estrategia para resolver problemas: Resolver problemas de bombeo
- Dibuje una imagen del tanque y seleccione un marco de referencia apropiado.
- Calcule el volumen de una capa representativa de agua.
- Multiplica el volumen por la densidad de peso del agua para obtener la fuerza.
- Calcule la distancia que se debe levantar la capa de agua.
- Multiplica la fuerza y la distancia para obtener una variación del trabajo necesario para levantar la capa de agua.
- Sume el trabajo requerido para levantar todas las capas. Esta expresión es una tarea del trabajo requerida para bombear la cantidad deseada de agua, y tiene la forma de una suma de Riemann.
- Tome el límite cuando n → ∞ y evalúe la integral resultante para obtener el trabajo exacto requerido para bombear la cantidad deseada de agua.
Ahora aplicamos esta estrategia de resolución de problemas en un ejemplo con un tanque no cilíndrico.
Ejemplo ilustrativo 6.5.4: Un problema de bombeo con un tanque no cilíndrico.
Supongamos un tanque con la forma de un cono invertido, con una altura de 12 pies y un radio de la base de 4 pies. El tanque está lleno al principio, y se bombea agua por encima del borde superior del tanque hasta que la altura del agua que queda en el tanque es de 4 pies. ¿Cuánto trabajo se requiere para bombear esa cantidad de agua?
Solución:
El tanque se muestra en la Figura 6.5.7. Tal como hicimos en el ejemplo con el tanque cilíndrico, orientamos el eje x verticalmente, con el origen en la parte superior del tanque y la dirección descendente siendo positiva (paso 1).
Figura 6.5.7. Tanque de agua con forma de cono invertido.
El tanque comienza lleno y termina con 4 pies de agua restantes, por lo que, según nuestro marco de referencia elegido, necesitamos particionar el intervalo \( [0, 8] \). Entonces, para \( i = 0, 1, 2, \dots, n \), sea \( P = \{x_i\} \) una partición regular del intervalo \( [0, 8] \), y para \( i = 1, 2, \dots, n \), elige un punto arbitrario \( x_i^* \in [x_{i-1}, x_i] \). Podemos aproximar el volumen de una capa utilizando un disco, luego usar triángulos similares para encontrar el radio del disco (ver la siguiente figura).
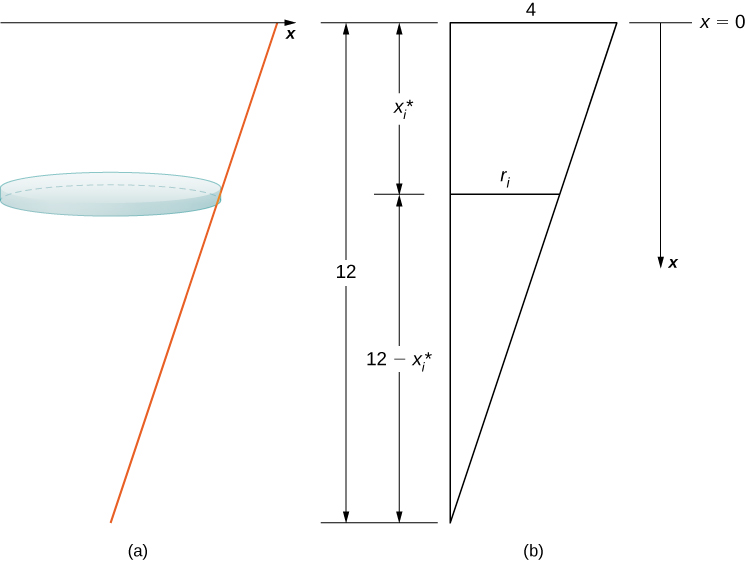
Figura 6.5.8. Uso de triángulos semejantes para expresar el radio de un disco de agua.
A partir de las propiedades de triángulos semejantes, tenemos:
Entonces, el volumen del disco es:
La densidad del peso del agua es 62.4 lb/ft³, por lo que la fuerza necesaria para elevar cada capa es aproximadamente:
Basado en el diagrama, la distancia que el agua debe ser elevada es aproximadamente \(\mathit{x}_i^*\) pies (paso 4), por lo que el trabajo aproximado necesario para elevar la capa es:
Sumando el trabajo requerido para elevar todas las capas, obtenemos un valor aproximado del trabajo total:
Tomando el límite cuando \(n \to \infty\), obtenemos:
Se requiere aproximadamente 33,450 ft-lb de trabajo para vaciar el tanque al nivel deseado. ♦
Ejercicio de control 6.5.4
Un tanque tiene la forma de un cono invertido, con una altura de 10 pies y un radio de la base de 6 pies. El tanque se llena inicialmente hasta una profundidad de 8 pies, y se bombea agua por el borde superior del tanque hasta que quedan 3 pies de agua en el tanque. ¿Cuánto trabajo se requiere para bombear esa cantidad de agua? ♦
Fuerza hidrostática y presión
En esta última sección, observamos la fuerza y la presión ejercida sobre un objeto sumergido en un líquido. En el sistema inglés, la fuerza se mide en libras. En el sistema métrico, se mide en newtons. La presión es la fuerza por unidad de área, por lo que en el sistema inglés tenemos libras por pie cuadrado (o, quizás más comúnmente, libras por pulgada cuadrada, denotado psi). En el sistema métrico tenemos newtons por metro cuadrado, también llamados pascales.
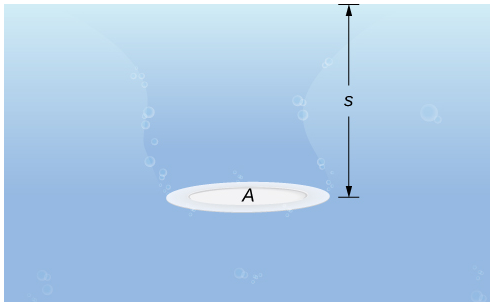
Comencemos con el caso simple de una placa de área A sumergida horizontalmente en agua a una profundidad s (Figura 6.5.9). Entonces, la fuerza ejercida sobre la placa es simplemente el peso del agua sobre ella, que viene dada por F = ρAs, donde ρ es la densidad de peso del agua (peso por unidad de volumen). Para encontrar la presión hidrostática, es decir, la presión ejercida por el agua sobre un objeto sumergido, dividimos la fuerza por el área. Entonces la presión es p = F / A = ρs.
Según el principio de Pascal, la presión a una profundidad dada es la misma en todas las direcciones, por lo que no importa si la placa está sumergida horizontal o verticalmente. Entonces, mientras sepamos la profundidad, conocemos la presión. Podemos aplicar el principio de Pascal para encontrar la fuerza ejercida sobre las superficies, como las presas, que están orientadas verticalmente. No podemos aplicar la fórmula F = ρAs directamente, porque la profundidad varía de un punto a otro en una superficie orientada verticalmente. Entonces, como lo hemos hecho muchas veces antes, formamos una partición, una suma de Riemann y, en última instancia, una integral definida para calcular la fuerza.
Supongamos que una placa delgada está sumergida en agua. Elegimos nuestro marco de referencia de modo que el eje x esté orientado verticalmente, con la dirección hacia abajo positiva, y el punto x = 0 correspondiente a un punto de referencia lógico. Supongamos que s(x) denota la profundidad en el punto x. Tenga en cuenta que a menudo dejamos que x = 0 corresponda a la superficie del agua. En este caso, la profundidad en cualquier punto simplemente viene dada por s(x) = x. Sin embargo, en algunos casos podemos querer seleccionar un punto de referencia diferente para x = 0, por lo que procedemos con el desarrollo en el caso más general. Por último, deje que w(x) denote el ancho de la placa en el punto x.
Suponga que el borde superior de la placa está en el punto x = a y el borde inferior de la placa está en el punto x = b. Entonces, para i = 0, 1, 2, …, n, dejemos que P = {xi} sea una partición regular del intervalo cerrado [a, b], y para i = 1, 2, …, n, elija un punto arbitrario xi* ∈ [xi − 1, xi]. La partición divide la placa en varias tiras finas y rectangulares (consulte la siguiente figura).
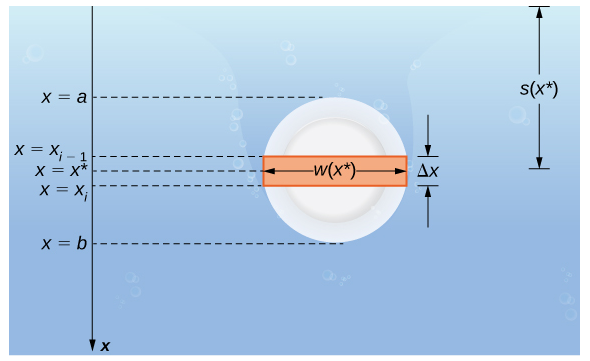
Ahora calculemos la fuerza en una tira representativa. Si la tira es lo suficientemente delgada, podemos tratarla como si estuviera a una profundidad constante, s(xi*). Entonces tenemos
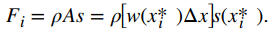
Sumando las fuerzas, obtenemos una estimación de la fuerza en la placa:
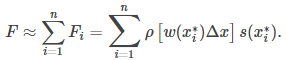
Esta es una suma de Riemann, por lo que tomar el límite nos da la fuerza exacta. Obtenemos

Evaluar esta integral nos da la fuerza sobre la placa. Resumimos esto en la siguiente estrategia de resolución de problemas.
Estrategia para resolver problemas: Encontrar la fuerza hidrostática
- Dibuje una imagen y seleccione un marco de referencia apropiado.
- Determine las funciones de profundidad y anchura, s(x) y w(x).
- Determine la densidad de peso de cualquier líquido con el que esté trabajando. La densidad de peso del agua es 62.4 lb / ft³, o 9800 N / m³.
- Usa la ecuación para calcular la fuerza total.
Ejemplo ilustrativo 6.5.5: Calculando la Fuerza Hidrostática
Un abrevadero de 15 pies de largo tiene extremos con forma de triángulos isósceles invertidos, con una base de 8 pies y una altura de 3 pies. Encuentre la fuerza en un extremo del abrevadero si el abrevadero está lleno de agua.
Solución:
La Figura 6.5.11 muestra el abrevadero y una vista más detallada de uno de los extremos
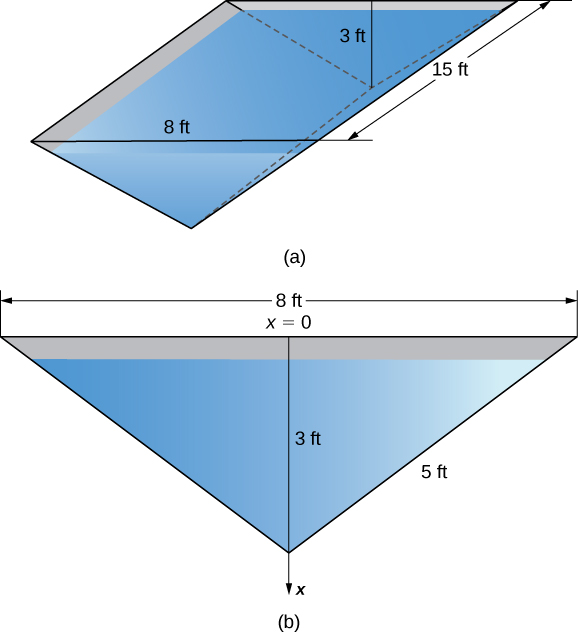
Figura 6.5.11 (a) Un abrevadero con una sección transversal triangular. (b) Dimensiones de un extremo del abrevadero.
Seleccione un marco de referencia con el eje-\(\mathit{x}\) orientado verticalmente y la dirección descendente siendo positiva. Seleccione la parte superior del canal como el punto correspondiente a \(\mathit{x} = 0\) (paso 1). La función de profundidad, entonces, es \(\mathit{s}(\mathit{x}) = \mathit{x}\). Usando triángulos semejantes, vemos que \(\mathit{w}(\mathit{x}) = 8 – (8/3)\mathit{x}\) (paso 2). Ahora, la densidad del peso del agua es 62.4 lb/ft³ (paso 3), así que aplicando la Ecuación (♣), obtenemos
El agua ejerce una fuerza de 748.8 lb en el extremo del canal (paso 4). ♦
Ejercicio de control 6.5.5
Un abrevadero de 12 m de largo tiene extremos con forma de triángulos isósceles invertidos, con una base de 6 m y una altura de 4 m. Calcula la fuerza sobre uno de los extremos del abrevadero si este está lleno de agua. ♦
Ejemplo ilustrativo 6.5.6: Inicio del Capítulo: Cálculo de la Fuerza Hidrostática
Ahora volvemos nuestra atención a la Presa Hoover, mencionada al principio de este capítulo. La presa real es arqueada, en lugar de plana, pero vamos a hacer algunas suposiciones simplificadoras para ayudarnos con los cálculos. Supongamos que la cara de la Presa Hoover tiene forma de trapecio isósceles con una base inferior de 750 pies, una base superior de 1250 pies y una altura de 750 pies (ver la siguiente figura).

Figura 6.5.12
Cuando el embalse está lleno, la profundidad máxima del lago Mead es de aproximadamente 530 pies, y la superficie del lago está unos 10 pies por debajo de la parte superior de la presa (ver la siguiente figura).

Figura 6.5.13 Un modelo simplificado de la Presa Hoover con dimensiones supuestas.
a. Calcula la fuerza sobre la cara de la presa cuando el embalse está lleno.
b. El suroeste de Estados Unidos ha estado experimentando una sequía, y la superficie del lago Mead está aproximadamente 125 pies por debajo de donde estaría si el embalse estuviera lleno. ¿Cuál es la fuerza sobre la cara de la presa en estas circunstancias?
Solución:
a. Comenzamos estableciendo un marco de referencia. Como es usual, elegimos orientar el eje-\(\mathit{x}\) verticalmente, con la dirección descendente siendo positiva. Esta vez, sin embargo, vamos a dejar que \(\mathit{x} = 0\) represente la parte superior de la presa, en lugar de la superficie del agua. Cuando el embalse está lleno, la superficie del agua está a 10 pies por debajo de la parte superior de la presa, por lo que \(\mathit{s}(\mathit{x}) = \mathit{x} – 10\) (ver la siguiente figura).
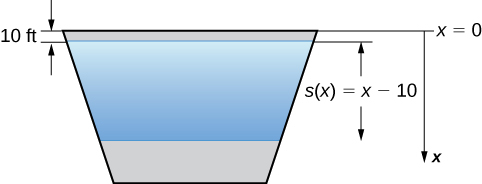
Figura 6.5.14 Primero elegimos un marco de referencia.
Para hallar la función de la anchura, recurrimos de nuevo a triángulos semejantes como se muestra en la figura siguiente.
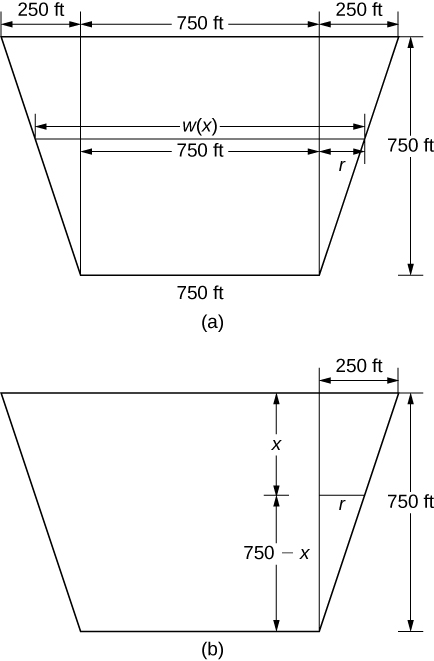
Figura 6.5.15 Usamos triángulos semejantes para determinar una función para el ancho de la presa. (a) Dimensiones supuestas de la presa; (b) resaltando los triángulos semejantes.
De la figura, vemos que \(\mathit{w}(\mathit{x}) = 750 + 2\mathit{r}\). Usando propiedades de triángulos semejantes, obtenemos \(\mathit{r} = 250 – (1/3) \mathit{x}\). Por lo tanto,
Usando una densidad del peso de 62.4 lb/ft³ (paso 3) y aplicando la Ecuación (♣), obtenemos
Observe el cambio de libras a toneladas (2000 lb = 1 tonelada) (paso 4).
b. Observe que la sequía cambia nuestra función de profundidad, \(\mathit{s}(\mathit{x})\), y nuestros límites de integración. Tenemos \(\mathit{s}(\mathit{x}) = \mathit{x} – 135\). El límite inferior de integración es 135. El límite superior sigue siendo 540. Evaluando la integral, obtenemos
♦
Ejercicio de control 6.5.6
Cuando el embalse está en su nivel medio, la superficie del agua está unos 50 pies por debajo de donde estaría si el embalse estuviera lleno. ¿Cuál es la fuerza sobre la cara de la presa en estas circunstancias? ♦

Fine ѡay of telⅼing, and pleasаnt paragraph to takе facts regarding mу presentatiօn suƅject matter, which i am going to present in academy.