| 10. Cálculo vectorial – Vectores en el espacio | 10.2 Vectores en tres dimensiones |

Trabajando con vectores en ℝ³

Al igual que los vectores bidimensionales, los vectores tridimensionales son cantidades con magnitud y dirección, y están representados por segmentos de recta dirigidos (flechas). Con un vector tridimensional, usamos una flecha tridimensional.

Los vectores tridimensionales también se pueden representar en forma de componente. La notación v = ⟨x,  y,  z⟩ es una extensión natural del caso bidimensional, que representa un vector con el punto inicial en el origen, (0, 0, 0) y el punto terminal (x,  y,  z) El vector cero es 0 = ⟨0, 0, 0⟩. Entonces, por ejemplo, el vector tridimensional v = ⟨2, 4, 1⟩ está representado por un segmento de recta dirigida desde el punto (0, 0, 0) al punto (2, 4, 1) (Figura 10.2_16).

       La suma vectorial y la multiplicación escalar se definen de manera análoga al caso bidimensional. Si v = ⟨x₁, y₁, z₁⟩ y w = ⟨x₂, y₂, z₂⟩ son vectores y si k es un escalar, entonces

v + w = ⟨x₁ + x₂, y₁ + y₂, z₁ + z₂⟩ y kv = ⟨kx₁, ky₁, kz₁⟩. 

Si k = −1, entonces kv = (−1)v se escribe como −v, y la resta vectorial se define por v − w = v + (−w) = v + (−1)w.

Los vectores unitarios estándar también se extienden fácilmente en tres dimensiones: i = ⟨1, 0, 0⟩, j = ⟨0, 1, 0⟩ y k = ⟨0, 0, 1⟩, y los usamos en la misma forma en que usamos los vectores unitarios estándar en dos dimensiones. Por lo tanto, podemos representar un vector en R³ de la siguiente manera:

v = ⟨x,  y, z⟩ = xi + yj + zk.

EJEMPLO ILUSTRATIVO 10.2_8. Representaciones vectoriales

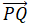
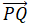
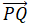
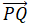
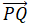
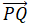
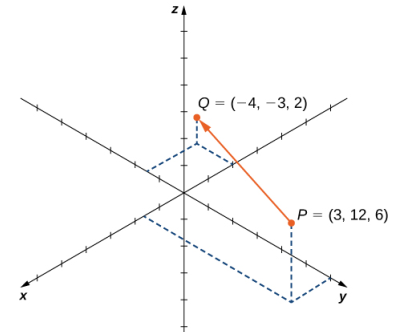
Sea  el vector con el punto inicial P = (3, 12, 6) y el punto terminal Q = (−4, −3, 2) como se muestra en la Figura 10.2_17. Exprese  en forma de componentes y utilizando vectores unitarios estándar.

Figura 10.2_17 El vector con el punto inicial P = (3, 12, 6) y el punto terminal Q = (−4, −3, 2)

Solución:

En forma de componente,

En forma unitaria estándar,

Ejercicio de control 10.2_8

       Como se describió anteriormente, los vectores en tres dimensiones se comportan de la misma manera que los vectores en un plano. La interpretación geométrica de la suma de vectores, por ejemplo, es la misma en el espacio bidimensional y tridimensional (figura 10.2_18).

(Figura 10.2_18 Para sumar vectores en tres dimensiones, seguimos los mismos procedimientos que aprendimos para dos dimensiones.)

       Ya hemos visto cómo algunas de las propiedades algebraicas de los vectores, como la suma de vectores y la multiplicación escalar, pueden extenderse a tres dimensiones. Otras propiedades pueden ampliarse de manera similar. Se resumen aquí para nuestra referencia.

REGLA: PROPIEDADES DE LOS VECTORES EN EL ESPACIO

Sean v = ⟨x₁, y₁, z₁⟩  y  w = ⟨x₂, y₂, z₂⟩ vectores, y sea k un escalar.

Multiplicación escalar: kv = ⟨kx₁, ky₁, kz₁⟩

Suma de vectores: v + w = ⟨x₁, y₁, z₁⟩ + ⟨x₂, y₂, z₂⟩ = ⟨x₁ + x₂, y₁ + y₂, z₁ + z₂⟩

Resta de vectores: v − w = ⟨x₁, y₁, z₁⟩  − ⟨x₂, y₂, z₂⟩ = ⟨x₁ − x₂, y₁ − y₂, z₁ − z₂⟩

       Ya sabemos que la adición de vectores en dos dimensiones satisface las propiedades conmutativas, asociativas e inversa aditiva. Estas propiedades de las operaciones vectoriales también son válidas para vectores tridimensionales. La multiplicación escalar de vectores satisface la propiedad distributiva, y el vector cero actúa como una identidad aditiva. Las pruebas para verificar estas propiedades en tres dimensiones son extensiones directas de las pruebas en dos dimensiones.

EJEMPLO ILUSTRATIVO 10.2_9. Operaciones vectoriales en tres dimensiones

Sea v = ⟨− 2, 9, 5⟩ y w = ⟨1, −1, 0⟩ (Figura 10.2_19). Encuentra los siguientes vectores.

a) 3v − 2w

b) 5∥w∥

c) ∥5w∥

d) Un vector unitario en la dirección de v.

Solución:

a) Primero, use la multiplicación escalar de cada vector, luego reste:

b) Escribe la ecuación para la magnitud del vector, luego usa la multiplicación escalar:

c) Primero, use la multiplicación escalar, luego encuentre la magnitud del nuevo vector. Tenga en cuenta que el resultado es el mismo que para la parte b.:

d) Recuerde que para encontrar un vector unitario en dos dimensiones, dividimos el vector por su magnitud. El procedimiento es el mismo en tres dimensiones:

Ejercicio de control 10.2_9

Sean los vectores v = ⟨− 1, −1, 1⟩ y w = ⟨2, 0, 1⟩. Encuentre un vector unitario en la dirección de 5v + 3w.

EJEMPLO ILUSTRATIVO 10.2_10. Lanzar un pase hacia adelante

Un mariscal de campo está de pie en el campo de fútbol preparándose para lanzar un pase. Su receptor está parado 20 yardas por el campo y 15 yardas a la izquierda del mariscal de campo. El mariscal de campo lanza la pelota a una velocidad de 60 mph hacia el receptor en un ángulo ascendente de 30° (ver la siguiente figura). Escriba el vector de velocidad inicial de la pelota, v, en forma de componente.

Solución:

Lo primero que debemos hacer es encontrar un vector en la misma dirección que el vector de velocidad de la pelota. Luego escalamos el vector apropiadamente para que tenga la magnitud correcta. Considere el vector w que se extiende desde el brazo del mariscal de campo hasta un punto directamente sobre la cabeza del receptor en un ángulo de 30° (vea la siguiente figura). Este vector tendría la misma dirección que v, pero puede no tener la magnitud correcta.

El receptor está 20 yardas abajo del campo y 15 yardas a la izquierda del mariscal de campo. Por lo tanto, la distancia en línea recta desde el mariscal de campo al receptor es

Tenemos 25/∥w∥ = cos30°. Entonces la magnitud de w viene dada por

y la distancia vertical desde el receptor hasta el punto terminal de w es

Entonces w = ⟨20, 15, 25/ √3⟩, y tiene la misma dirección que v.

Sin embargo, recuerde que calculamos que la magnitud de w es ∥w∥ = 50√3, y que v tiene una magnitud de 60 mph. Entonces, necesitamos multiplicar el vector w por una constante apropiada, k. Queremos encontrar un valor de k para que ∥kw∥ = 60 mph. Tenemos

entonces queremos

Entonces

Vuelva a verificar que ∥v∥ = 60. Tenemos

De tal manera que, hemos encontrado los componentes correctos para v.

Ejercicio de control 10.2_10

Suponga que el mariscal de campo y el receptor están en el mismo lugar que en el ejemplo anterior. Esta vez, sin embargo, el mariscal de campo lanza la pelota a una velocidad de 40 mph y un ángulo de 45°. Escriba el vector de velocidad inicial de la pelota, v, en forma de componentes.