Álgebra lineal con aplicaciones

| 2. Álgebra de matrices | Ejercicios propuestos para el Capítulo 2.1 |

2.1.  Suma, multiplicación escalar y transposición de matrices

    Un arreglo rectangular de números se llama matriz (el plural es matrices), y los números se llaman entradas de la matriz. Las matrices generalmente se denotan con letras mayúsculas: A, B, C, etc. Por lo tanto,

son matrices. Claramente, las matrices vienen en varias formas dependiendo del número de filas y columnas. Por ejemplo, la matriz A que se muestra tiene 2 filas y 3 columnas. En general, una matriz con m filas y n columnas se denomina matriz m × n o tiene un tamaño m × n. Por lo tanto, las matrices A, B y C anteriores tienen tamaños 2 × 3, 2 × 2 y 3 × 1, respectivamente. Una matriz de tamaño 1 × n se llama matriz fila, mientras que una de tamaño m × 1 se llama matriz columna. Las matrices de tamaño n × n para algunos n se llaman matrices cuadradas.

Cada entrada de una matriz se identifica por la fila y la columna en la que se encuentra. Las filas están numeradas de arriba hacia abajo y las columnas están numeradas de izquierda a derecha. Entonces la entrada (i, j) de una matriz es el número que se encuentra simultáneamente en la fila i y la columna j. Por ejemplo,

Una notación especial se usa comúnmente para las entradas de una matriz. Si A es una matriz m × n, y si la entrada (i, j) de A se denota como a_ij, entonces A se denota de la siguiente manera:

Esto generalmente se denota simplemente como A = [a_ij]. Por lo tanto, a_ij es la entrada en la fila i y la columna j de A. Por ejemplo, se escribe una matriz 3 × 4 en esta notación como

Vale la pena señalar una convención sobre filas y columnas: las filas se mencionan antes que las columnas.
Por ejemplo:

• Si una matriz tiene un tamaño m × n, tiene m filas y n columnas.
• Si hablamos de la entrada (i, j) de una matriz, tal entrada se encuentra en la fila i y la columna j.
• Si una entrada se denota como a_ij, el primer subíndice i se refiere a la fila y el segundo subíndice j a la columna en la que se encuentra a_ij.

Igualdad de matrices

Dos puntos (x₁, y₁) y (x₂, y₂) en el plano son iguales si y sólo si tienen las mismas coordenadas, es decir x₁ = x₂ e y₁ = y₂. Del mismo modo, dos matrices A y B se llaman iguales (escritas A = B) si y sólo si:

1. Tienen el mismo tamaño.
2. Las entradas correspondientes son iguales.

       Si las entradas de A y B están escritas en la forma A = [a_ij], B = [b_ij], descritas anteriormente, entonces la segunda condición toma la siguiente forma:

Ejemplo ilustrativo 2.1_1

Dadas las siguientes matrices

discuta la posibilidad de que A = B, B = C, A = C.

Solución:
A = B es imposible porque A y B son de diferentes tamaños: A es de 2 × 2 mientras que B es de 2 × 3. Del mismo modo, B = C es imposible. Pero A = C es posible siempre que las entradas correspondientes sean iguales:

significa que a = 1, b = 0, c = −1 y d = 2. ◊

Suma de matrices

Definición 2.1.1 Adición de matrices

Si A y B son matrices del mismo tamaño, su suma, denotada por A + B, es la matriz formada al adicionar las entradas correspondientes.

Si A = [a_ij] y B = [b_ij], la suma de A y B toma la forma

Tenga en cuenta que la suma no está definida para matrices de diferentes tamaños.

Ejemplo ilustrativo 2.1_2

Si

y

calcule A + B.

Solución:

Ejemplo ilustrativo 2.1_3

Encuentre los valores de a, b y c si [a  b  c] + [c  a  b] = [3  2  −1].

Solución:
Sume las matrices en el lado izquierdo para obtener

[a + c   b + a   c + b] = [3  2  −1]

Debido a que las entradas correspondientes deben ser iguales, esto da tres ecuaciones: a + c = 3, b + a = 2 y c + b = −1, cuya solución es a = 3, b = −1, c = 0. ◊

Dos propiedades algebraicas de la suma de matrices

Si A, B y C son matrices del mismo tamaño, entonces

A + B = B + A	Ley conmutativa
A + (B + C) = (A + B) + C	Ley asociativa

De hecho, si A = [aij] y B = [bij], entonces las entradas (i, j) de A + B y B + A son, respectivamente, aij + bij y bij + aij. Como las entradas son iguales para todos los i y j, obtenemos (teniendo presente la ley conmutativa en la suma de números reales)

La ley asociativa se verifica de manera similar.

    La matriz m × n en la que cada entrada es cero se llama matriz cero de m × n y se denota como 0 (o 0_mn si es importante enfatizar el tamaño). Por lo tanto,

0 + X = X

se cumple para todas las matrices X de m × n.

    El negativo de una matriz A de m × n (escrito −A) se define como la matriz de tamaño m × n obtenida al multiplicar cada entrada de A por −1. Si A = [a_ij], el negativo de A se denota por −A = [−a_ij]. Por lo tanto,

A + (−A) = 0

se cumple para todas las matrices A donde, por supuesto, 0 es la matriz cero del mismo tamaño que A.

    Una noción estrechamente relacionada con la suma es la de restar matrices. Si A y B son dos matrices de tamaño m × n, su diferencia A − B se define por

A − B = A + (−B)

Tenga en cuenta que si A = [a_ij]  y  B = [b_ij], entonces

es la matriz de tamaño m × n formada restando las entradas correspondientes.

Ejemplo ilustrativo 2.1_4

Dadas las matrices

Calcule −A, A − B y A + B − C.

Solución:

Ejemplo ilustrativo 2.1_5

Resolver la ecuación

donde X es una matriz.

Solución:

Resolvemos una ecuación numérica a + x = b restando el número a de ambos lados para obtener x = b − a. Esto también funciona para ecuaciones con matrices. Para resolversimplemente resta la matrizde ambos lados de la igualdad para obtenerEl lector debe verificar que esta matriz X realmente satisfaga la ecuación original. ◊

     La solución hallada en el ejemplo 2.1_5 que satisface la ecuación de matrices A + X = B, se obtiene directamente mediante sustracción de matrices: X = B − A. Esta capacidad de trabajar con matrices como entidades se encuentra en el corazón del álgebra matricial.

    Es importante notar que los tamaños de las matrices involucradas en algunos cálculos a menudo están determinados por el contexto. Por ejemplo, si

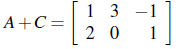
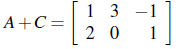
entonces, A y C deben tener el mismo tamaño (para que A + C tenga sentido), y ese tamaño debe ser 2×3 (para que la suma sea 2×3). Por simplicidad, a menudo omitiremos la referencia a tales hechos cuando sean claros por el contexto.

Multiplicación escalar

En la eliminación gaussiana, multiplicar una fila de una matriz por un número k significa multiplicar cada entrada de esa fila por k.

 

Definición 2.2  Multiplicación escalar de matrices

De manera más general, si A es cualquier matriz y k es cualquier número, el múltiplo escalar kA es la matriz obtenida de A al multiplicar cada entrada de A por k.

Si A = [a_ij], entonces

kA = [ka_ij] 

♦

 

Por ejemplo, de acuerdo con la multiplicación escalar, 1A = A y (−1)A = −A para cualquier matriz A.

 

      El término escalar surge aquí porque el conjunto de números del que se toman las entradas se suele denominar conjunto de escalares (se debe diferenciar entre magnitudes escalares y magnitudes vectoriales). Hemos estado usando números reales como escalares, pero igualmente bien podríamos haber estado usando números complejos.

Ejemplo ilustrativo 2.1_6

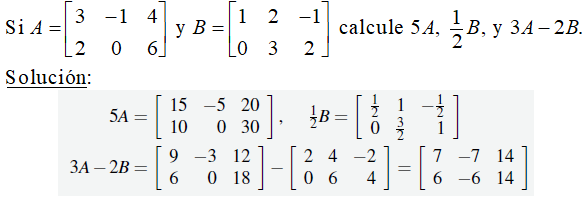
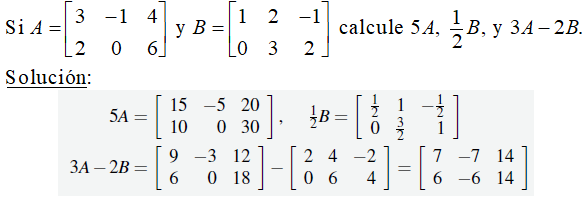
      Si A es cualquier matriz, tenga en cuenta que k A es del mismo tamaño que A para todos los escalares k. También tenemos que

0A = 0   y   k 0 = 0

porque la matriz cero tiene todas las entradas cero. En otras palabras, kA = 0 si k = 0 o A = 0. El inverso de esta afirmación también es cierto, como muestra el ejemplo 2.1_7.

Ejemplo ilustrativo 2.1_7

Si kA = 0, demuestre que k = 0 o A = 0.

Solución:

Escriba A = a_ij de modo que kA = 0 signifique ka_ij = 0 para todo i y j. Si k = 0, no hay nada que hacer. Si k ≠ 0, entonces ka_ij = 0 implica que a_ij = 0 para todo i y j; es decir, A = 0.  ◊

       Para referencia futura, las propiedades básicas de la suma de matrices y la multiplicación escalar se enumeran en el Teorema 2.1.1.

Teorema 2.1.1

Sean A, B y C matrices arbitrarias de tamaño m × n donde m y n son fijos. Sean k y p números reales arbitrarios. Luego

1.  A + B = B + A.
2.  A + (B + C) = (A + B) + C.
3.  Hay una matriz 0 de tamaño m × n, tal que 0 + A = A para cada A.
4.  Para cada A hay una matriz m × n, −A, tal que A + (−A) = 0.
5.  k (A + B) = k A + k B.
6.  (k + p) A = k A + p A.
7.  (k p) A = k (p A).
8.  1A = A.

♦

Prueba.  Las propiedades 1 a 4 se dieron previamente. Para comprobar la propiedad 5, deje que A = [aij]  y  B = [aij]  denoten matrices del mismo tamaño. Entonces A + B = [aij + bij], como antes, entonces la entrada (i, j) de k(A + B) es k(aij + bij) = kaij + kaij Pero esta es precisamente la entrada (i, j) de kA + kB, y se sigue que k(A + B) = kA + kB. Las otras propiedades se pueden verificar de manera similar; los detalles se dejan al lector.  ♦

      Las propiedades del teorema 2.1.1 nos permiten hacer cálculos con matrices de la misma manera que se realizan los cálculos numéricos. Para empezar, la propiedad 2 implica que la suma

(A + B) + C = A + (B + C)

es la misma sin importar cómo se forme la asociación y por eso se escribe como A + B + C. Del mismo modo, la suma

A + B + C + D

es independiente de cómo se asocie; por ejemplo, es igual a (A + B) + (C + D)  y  A + [B + (C + D)].
Además, la propiedad 1 asegura que, por ejemplo

B + D + A + C = A + B + C + D

En otras palabras, el orden en que se agregan las matrices no importa. Una observación similar se aplica a las sumas de cinco (o más) matrices.

      Las propiedades 5 y 6 del teorema 2.1.1 se denominan leyes distributivas para la multiplicación escalar y se extienden a sumas de más de dos términos. Por ejemplo,

k (A + B − C) = kA + kB − kC
(k + p − m) A = kA + pA − mA

Observaciones similares son válidas para más de tres sumandos. Estos hechos, junto con las propiedades 7 y 8, nos permiten simplificar expresiones al recopilar términos semejantes, expandir y tomar factores comunes exactamente de la misma manera en que se manipulan las expresiones algebraicas que involucran variables y números reales. El siguiente ejemplo ilustra estas técnicas.

Ejemplo ilustrativo 2.1_8

Simplifica 2(A + 3C) − 3(2C − B) − 3[2(2A + B − 4C) − 4(A − 2C)] donde A, B y C son todas matrices del mismo tamaño.

Solución:

La reducción procede como si A, B y C fueran variables.

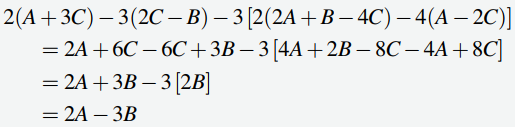
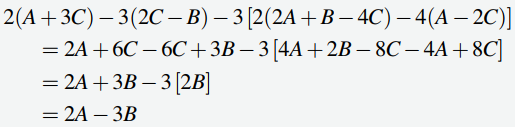
Transposición de una matriz

      Muchos resultados sobre una matriz A involucran las filas de A, y el resultado correspondiente para las columnas se deriva de una manera análoga, esencialmente reemplazando la palabra fila por la palabra columna en todas partes. La siguiente definición se hace teniendo en cuenta tales aplicaciones.

Definición 2.3. Transposición de una matriz

Si A es una matriz de tamaño m × n, la transpuesta de A, escrita A^T, es la matriz de tamaño n × m donde el elemento en la fila 𝑖 y la columna 𝑗 de 𝐴^𝑇 es el elemento en la fila 𝑗 y la columna 𝑖 de $A$. Formalmente, si 𝐴 = [𝑎_𝑖𝑗], entonces 𝐴^𝑇 = [𝑎_𝑗𝑖]. ♦

En otras palabras, la primera fila de A^T es la primera columna de A (es decir, consta de las entradas de la columna 1 en orden). De manera similar, la segunda fila de A^T es la segunda columna de A, y así sucesivamente.  

Ejemplo ilustrativo 2.1_9

Escriba la transpuesta de cada una de las siguientes matrices.

Solución:

◊

      Si A = a_ij es una matriz, escriba A^T = [b_ij]. Entonces b_ij es el j-ésimo elemento de la i-ésima fila de A^T y también lo es el j-ésimo elemento de la i-ésima columna de A. Esto significa b_ij = a_ji, por lo que la definición de A^T se puede establecer de la siguiente manera:

Si A = a_ij, entonces A^T = a_ji.              (2.1)

Esto es útil para verificar las siguientes propiedades de transposición.

Teorema 2.1.2

Suponga que A y B denotan matrices del mismo tamaño, y k denota una escalar. Entonces

1.  Si A es una matriz m × n, entonces A^T es una matriz n × m.
2.  (A^T)^T = A.
3.  (kA)^T = kA^T.
4.  (A + B)^T = A^T + B^T.  ◊

Prueba. La propiedad 1 es parte de la definición de AT y la propiedad 2 se deduce de (2.1). En cuanto a la propiedad 3: si A = aij, entonces kA = kaij, entonces (2.1) da Finalmente, si B = bij, entonces A + B = cij donde cij = aij + bij Entonces (2.1) da la Propiedad 4:

      Hay otra forma útil de pensar en la transposición. Si A = [a_ij] es una matriz m × n, los elementos a₁₁, a₂₂, a₃₃, … se llaman la diagonal principal de A. Por lo tanto, la diagonal principal se extiende hacia abajo y hacia la derecha desde la esquina superior izquierda de la matriz A; se describe en los siguientes ejemplos:

Por tanto, formar la transposición de una matriz A puede verse como “voltear” A alrededor de su diagonal principal, o como “rotar” A 180º alrededor de la línea que contiene la diagonal principal. Esto hace que la propiedad 2 del teorema 2.1.2 sea evidente.

Ejemplo ilustrativo 2.1_10

Resuelve para A si 

Solución:

Usando el teorema 2.1.2, el lado izquierdo de la ecuación es

Por lo tanto, la ecuación se convierte en

Por lo tanto

así que finalmente  ◊

Tenga en cuenta que el Ejemplo 2.1_10 también se puede resolver transponiendo primero ambos lados, luego resolviendo para A^T y, por lo tanto, obteniendo A = (A^T)^T. El lector debe hacer esto.

Matriz simétrica

La matriz  , así como la matriz D en el Ejemplo 2.1_9 tienen la propiedad de que D = D^T. Estas matrices son importantes; una matriz A se llama simétrica si A = A^T. Una matriz simétrica A es necesariamente cuadrada (si A es m × n, entonces A^T es n × m, entonces A = A^T fuerza n = m). El nombre proviene del hecho de que estas matrices exhiben una simetría sobre la diagonal principal. Es decir, las entradas que se encuentran directamente a lado y lado de la diagonal principal son iguales entre sí.

Por ejemplo  es simétrica cuando b = b′, c = c′  y  e = e′.

Ejemplo ilustrativo 2.1_11

Si A y B son matrices cuadradas de tamaño n × n simétricas, demuestre que A + B es simétrica.

Solución:

Tenemos A^T = A  y  B^T = B, entonces, por el Teorema 2.1.2, tenemos (A + B)^T = A^T + B^T = A + B. Por tanto, A + B es simétrica.

Ejemplo ilustrativo 2.1_12

Suponga que una matriz cuadrada A satisface A = 2A^T. Demuestre que necesariamente A = 0.

Solución:

Si iteramos la ecuación dada, el Teorema 2.1.2 da

Restar A de ambos lados da 3A = 0, entonces A = (1/3)(0) = 0.