| 7. Sucesiones y series infinitas | 7.1 Sucesiones | Enunciados de los Ejercicios 7.1 |

Soluciones de los Ejercicios 7.1: Sucesiones

1. Encuentre los primeros seis términos de la secuencia a_n = 1 + (−1)ⁿ  para  n ≥ 1 

Solución – Juan Beltrán:

La fórmula del término enésimo de la secuencia es: \[ \mathit{a}_n = 1 + (-1)^{\mathit{n}} \] Sustituimos los valores de \(\mathit{n}\) desde 1 hasta 6. \[ \] 1. Para \( \mathit{n} = 1 \): \[ \mathit{a}_1 = 1 + (-1)^1 = 1 – 1 = 0 \] 2. Para \( \mathit{n} = 2 \): \[ \mathit{a}_2 = 1 + (-1)^2 = 1 + 1 = 2 \] 3. Para \( \mathit{n} = 3 \): \[ \mathit{a}_3 = 1 + (-1)^3 = 1 – 1 = 0 \] 4. Para \( \mathit{n} = 4 \): \[ \mathit{a}_4 = 1 + (-1)^4 = 1 + 1 = 2 \] 5. Para \( \mathit{n} = 5 \): \[ \mathit{a}_5 = 1 + (-1)^5 = 1 – 1 = 0 \] 6. Para \( \mathit{n} = 6 \): \[ \mathit{a}_6 = 1 + (-1)^6 = 1 + 1 = 2 \] Por lo tanto, los primeros seis términos de la secuencia son: \[ \{0, 2, 0, 2, 0, 2, …\} \]

4. Encuentre los primeros seis términos de la secuencia a₁ = 1, a₂ = 1  y  a_{n + 2} = a_n + a_{n + 1}  para  n ≥ 1.

Solución – Juan Beltrán:

La secuencia está definida por: \[ a_1 = 1, \quad a_2 = 1 \] y la fórmula de recurrencia: \[ a_{n+2} = a_n + a_{n+1} \quad \text{para} \quad n \geq 1. \] Ahora, calculemos los primeros seis términos de la secuencia. \[ \] 1. Para \(n = 1\), tenemos: \[ a_1 = 1. \] 2. Para \(n = 2\), tenemos: \[ a_2 = 1. \] 3. Para \(n = 3\), aplicamos la fórmula de recurrencia: \[ a_3 = a_1 + a_2 = 1 + 1 = 2. \] 4. Para \(n = 4\), tenemos: \[ a_4 = a_2 + a_3 = 1 + 2 = 3. \] 5. Para \(n = 5\), tenemos: \[ a_5 = a_3 + a_4 = 2 + 3 = 5. \] 6. Para \(n = 6\), tenemos: \[ a_6 = a_4 + a_5 = 3 + 5 = 8. \] Por lo tanto, los primeros seis términos de la secuencia son: \[ \{1, 1, 2, 3, 5, 8, …\} \] Nota: Esta secuencia es conocida como la Secuencia de Fibonacci, donde cada término es la suma de los dos términos anteriores. \] Nota: Esta secuencia es conocida como la Secuencia de Fibonacci, donde cada término es la suma de los dos términos anteriores.

5. Encuentre una fórmula explícita para a_n donde a₁ = 1  y  a_{n − 1} + n  para  n ≥ 2.

Solución – Juan Beltrán:

La secuencia está definida por la relación de recurrencia: \[ a_1 = 1 \] y \[ a_n = a_{n-1} + n \quad \text{para} \quad n \geq 2. \] Para encontrar una fórmula explícita para \( a_n \), observamos cómo evoluciona la secuencia paso a paso. \[ \] 1. El primer término es dado: \[ a_1 = 1. \] 2. Para \( n = 2 \): \[ a_2 = a_1 + 2 = 1 + 2 = 3. \] 3. Para \( n = 3 \): \[ a_3 = a_2 + 3 = 3 + 3 = 6. \] 4. Para \( n = 4 \): \[ a_4 = a_3 + 4 = 6 + 4 = 10. \] 5. Para \( n = 5 \): \[ a_5 = a_4 + 5 = 10 + 5 = 15. \] Parece que los términos siguen la secuencia de números triangulares. De hecho, la relación recursiva describe una suma acumulada de números consecutivos. En términos de fórmula, podemos escribir: \[ a_n = 1 + 2 + 3 + \cdots + n. \] Esta es la suma de los primeros \( n \) números naturales, que se puede expresar de manera explícita usando la fórmula de la suma de una progresión aritmética: \[ a_n = \frac{n(n+1)}{2}. \] Por lo tanto, la fórmula explícita para el término enésimo \( a_n \) es: \[ \boxed{a_n = \frac{n(n+1)}{2}.} \]

7. Encuentre una fórmula a_n para el enésimo término de la secuencia aritmética cuyo primer término es a₁ = −3 tal que a_{n + 1} − a_n = 4 para n ≥ 1.

Solución – Juan Beltrán:

Para encontrar el término general \( a_n \) de una sucesión aritmética, usamos la fórmula general de las progresiones aritméticas: \[ a_n = a_1 + (n-1)d \] donde: \( \mathit{a}_1 \) es el primer término de la sucesión, \( \mathit{d} \) es la diferencia común entre los términos consecutivos, \( \mathit{n} \) es la posición del término en la sucesión. Datos conocidos: \[ \mathit{a}_1 = -3 \] \[\mathit{d} = 4 \quad \text{(porque \( a_{n+1} – a_n = 4 \))}\] Sustituyendo estos valores en la fórmula: \[ a_n = -3 + (\mathit{n}-1) \cdot 4 \] Simplificamos: \[ a_n = -3 + 4\mathit{n} – 4 \] \[a_n = 4\mathit{n} – 7\] Por lo tanto, la fórmula para el término enésimo es: \[ \boxed{a_n = 4\mathit{n} – 7} \]

8. Encuentre una fórmula a_n para el enésimo término de la secuencia geométrica cuyo primer término es a₁ = 1 tal que a_{n + 1}/a_n = 10 para n ≥ 1.

Solución – Juan Beltrán:

Para encontrar el término general \( a_n \) de una sucesión geométrica, usamos la fórmula general: \[ a_n = a_1 \cdot r^{n-1} \] donde: \( \mathit{a}_1 \) es el primer término de la sucesión, \( \mathit{r} \) es la razón común, \( \mathit{n} \) es la posición del término en la sucesión. Datos conocidos: \[ \mathit{a}_1 = 1 \] \[\mathit{r} = 10 \quad \text{(porque \( \frac{a_{n+1}}{a_n} = 10 \))}\] Sustituyendo estos valores en la fórmula general: \[ a_n = 1 \cdot 10^{\mathit{n}-1} \] Simplificamos: \[ a_n = 10^{\mathit{n}-1} \] Por lo tanto, la fórmula para el término general es: \[ \boxed{a_n = 10^{\mathit{n}-1}} \]

10. Encuentre una fórmula explícita para el enésimo término de la secuencia cuyos primeros términos son {0, 3, 8, 15, 24, 35, 48, 63, 80, 99,…}. (Sugerencia: primero agregue uno a cada término).

Solución – Juan Beltrán:

Para encontrar la fórmula explícita de esta secuencia, hacemos lo siguiente. \[ \] Paso 1: Sumar 1 a cada término de la secuencia original. La secuencia original es: \[ \{0, 3, 8, 15, 24, 35, 48, 63, 80, 99, \dots\} \] Al sumar 1 a cada término, se obtiene: \[ \{1, 4, 9, 16, 25, 36, 49, 64, 81, 100, \dots\} \] Paso 2: Reconocer el patrón en la secuencia transformada. La secuencia resultante (\( 1, 4, 9, 16, 25, \dots \)) corresponde a los cuadrados perfectos: \[ a_n + 1 = n^2 \] Paso 3: Despejar \( a_n \) en términos de \( n \). Restando uno en ambos lados, obtenemos: \[ a_n = n^2 – 1 \] Paso 4: Verificar la fórmula para los primeros términos. Para \( n = 1 \): \[ a_1 = 1^2 – 1 = 0 \] Para \( n = 2 \): \[ a_2 = 2^2 – 1 = 3 \] Para \( n = 3 \): \[ a_3 = 3^2 – 1 = 8 \] Para \( n = 4 \): \[ a_4 = 4^2 – 1 = 15 \] Para \( n = 5 \): \[ a_5 = 5^2 – 1 = 24 \] Los resultados coinciden con los términos de la secuencia original. Respuesta final: \[ \boxed{a_n = n^2 – 1} \]

13. Encuentre una fórmula para el término general a_n de la siguiente secuencia: {1, −1/3, 1/5, −1/7, …}.

Solución – Juan Beltrán:

La secuencia dada es: \[ \{1, -\frac{1}{3}, \frac{1}{5}, -\frac{1}{7}, \dots\} \] Podemos observar los siguientes patrones: \[ \] 1. El numerador es \(1\) en todos los términos. \[ \] 2. El denominador forma una secuencia de números impares: \[ 1, \, 3, \, 5, \, 7, \, \dots \] Esto puede expresarse como \(2\mathit{n} – 1\), donde \(\mathit{n}\) es el índice del término (\(\mathit{n} = 1, 2, 3, \dots\)). \[ \] 3. El signo alterna entre positivo y negativo: \[ +, \, -, \, +, \, -, \, \dots \] Esto puede representarse mediante \((-1)^{\mathit{n}+1}\), que tiene el siguiente comportamiento: \(-1\) para \(\mathit{n} = 2, 4, 6, \dots\) y \(+1\) para \(\mathit{n} = 1, 3, 5, \dots\). Combinando estas observaciones, el término general de la secuencia es: \[ a_{\mathit{n}} = \frac{(-1)^{\mathit{n}+1}}{2\mathit{n} – 1} \] Verificación: \[ \] Para \(\mathit{n} = 1\): \[ a_1 = \frac{(-1)^{1+1}}{2(1) – 1} = \frac{1}{1} = 1 \] Para \(\mathit{n} = 2\): \[ a_2 = \frac{(-1)^{2+1}}{2(2) – 1} = \frac{-1}{3} = -\frac{1}{3} \] Para \(\mathit{n} = 3\): \[ a_3 = \frac{(-1)^{3+1}}{2(3) – 1} = \frac{1}{5} \] Para \(\mathit{n} = 4\): \[ a_4 = \frac{(-1)^{4+1}}{2(4) – 1} = \frac{-1}{7} \] Los resultados coinciden con los términos de la secuencia. \[ \] Respuesta final: \[ \boxed{a_{\mathit{n}} = \frac{(-1)^{\mathit{n}+1}}{2\mathit{n} – 1}} \]

14. Encuentre una función f(n) que identifique el enésimo término a_n de las siguiente secuencia definida recursivamente, como a_n = f(n): a₁ = 1 y a_{n + 1} = −a_n para n ≥ 1.

Solución – Juan Beltrán:

La secuencia dada está definida recursivamente como: \[ a_1 = 1, \quad a_{\mathit{n}+1} = -a_{\mathit{n}} \quad \text{para } \mathit{n} \geq 1. \] Expandiendo los primeros términos, se obtiene: \[ a_1 = 1, \quad a_2 = -a_1 = -1, \quad a_3 = -a_2 = 1, \quad a_4 = -a_3 = -1, \quad a_5 = -a_4 = 1. \] Esto muestra que la secuencia alterna entre \(1\) y \(-1\). \[ \] Para valores impares de \(\mathit{n}\) (\(\mathit{n} = 1, 3, 5, \dots\)), \(a_{\mathit{n}} = 1\). \[ \] Para valores pares de \(\mathit{n}\) (\(\mathit{n} = 2, 4, 6, \dots\)), \(a_{\mathit{n}} = -1\). \[ \] El comportamiento alternante puede representarse con la potencia de \((-1)\): \[ a_{\mathit{n}} = (-1)^{\mathit{n}+1}. \] Verificación: \[ \] Para \(\mathit{n} = 1\), \[ a_1 = (-1)^{1+1} = (-1)^2 = 1. \] Para \(\mathit{n} = 2\), \[ a_2 = (-1)^{2+1} = (-1)^3 = -1. \] Para \(\mathit{n} = 3\), \[ a_3 = (-1)^{3+1} = (-1)^4 = 1. \] Para \(\mathit{n} = 4\), \[ a_4 = (-1)^{4+1} = (-1)^5 = -1. \] Los resultados coinciden con la secuencia dada. \[ \] De tal manera que \[ \boxed{f(\mathit{n}) = (-1)^{\mathit{n}+1}} \]

18. Encuentre una función f(n) que identifique el enésimo término a_n de las siguiente secuencia definida recursivamente, como a₁ = 1 y a_{n + 1} = a_n/2ⁿ para n ≥ 1.

Solución – Juan Beltrán:

Resolución paso a paso del problema:

1) Primero, analicemos los primeros términos de la secuencia:

\( \mathit{a}_1 = 1 \)

\( \mathit{a}_2 = \mathit{a}_1/2^1 = 1/2 \)

\( \mathit{a}_3 = \mathit{a}_2/2^2 = 1/2 \cdot 1/4 = 1/8 \)

\( \mathit{a}_4 = \mathit{a}_3/2^3 = 1/8 \cdot 1/8 = 1/64 \)

2) Observemos el patrón de los términos:

\( \mathit{a}_1 = 1 = 1/2^0 \)

\( \mathit{a}_2 = 1/2 = 1/2^1 \)

\( \mathit{a}_3 = 1/8 = 1/2^3 \)

\( \mathit{a}_4 = 1/64 = 1/2^6 \)

3) Parece que el exponente en el denominador sigue un patrón:

Para \( \mathit{a}_1 \): 0 = 0

Para \( \mathit{a}_2 \): 1 = 1

Para \( \mathit{a}_3 \): 3 = 1 + 2

Para \( \mathit{a}_4 \): 6 = 1 + 2 + 3

4) El patrón de exponentes sugiere que para \( \mathit{a}_n \), el exponente será la suma de los primeros \( (n-1) \) números naturales.

5) La suma de los primeros \( (n-1) \) números naturales viene dada por la fórmula: \( \frac{(n-1)n}{2} \)

6) Por lo tanto, la función \( \mathit{f}(n) \) será:

\[f(n) = \frac{1}{2^{\frac{(n-1)n}{2}}}\]

7) Comprobemos algunos términos:

– Para \( n=1 \): \( f(1) = 1/2^0 = 1 \) ✓

– Para \( n=2 \): \( f(2) = 1/2^1 = 1/2 \) ✓

– Para \( n=3 \): \( f(3) = 1/2^3 = 1/8 \) ✓

– Para \( n=4 \): \( f(4) = 1/2^6 = 1/64 \) ✓

De tal manera que:

\[ \boxed{f(n) = \frac{1}{2^{\frac{(n-1)n}{2}}}}\]

25. Suponga que lim_{n → ∞} a_n = 1, lim_{n → ∞} b_n = −1 y 0 <−b_n < a_n para todo n. Evalúe el siguiente límites, o indique que el límite no existe, o indique que no hay suficiente información para determinar si el límite existe: lim_{n → ∞} (a_n + b_n)/(a_n − b_n)

Solución – Juan Beltrán:

Dado el límite: \[ \lim_{\mathit{n} \to \infty} \frac{a_{\mathit{n}} + b_{\mathit{n}}}{a_{\mathit{n}} – b_{\mathit{n}}}, \] aplicaremos las propiedades del límite de una suma, resta y cociente para determinar su valor. \[\] Paso 1: Propiedad del límite de un cociente. Si el límite del numerador y el denominador existen, usamos la propiedad: \[ \lim_{\mathit{n} \to \infty} \frac{a_{\mathit{n}} + b_{\mathit{n}}}{a_{\mathit{n}} – b_{\mathit{n}}} = \frac{\lim_{\mathit{n} \to \infty} (a_{\mathit{n}} + b_{\mathit{n}})}{\lim_{\mathit{n} \to \infty} (a_{\mathit{n}} – b_{\mathit{n}})}. \] Paso 2: Propiedad del límite de una suma. \[ \] Numerador: \[ \lim_{\mathit{n} \to \infty} (a_{\mathit{n}} + b_{\mathit{n}}) = \lim_{\mathit{n} \to \infty} a_{\mathit{n}} + \lim_{\mathit{n} \to \infty} b_{\mathit{n}}. \] Dado que: \[ \lim_{\mathit{n} \to \infty} a_{\mathit{n}} = 1 \quad \text{y} \quad \lim_{\mathit{n} \to \infty} b_{\mathit{n}} = -1, \] tenemos: \[ \lim_{\mathit{n} \to \infty} (a_{\mathit{n}} + b_{\mathit{n}}) = 1 + (-1) = 0. \] Denominador: \[ \lim_{\mathit{n} \to \infty} (a_{\mathit{n}} – b_{\mathit{n}}) = \lim_{\mathit{n} \to \infty} a_{\mathit{n}} – \lim_{\mathit{n} \to \infty} b_{\mathit{n}}. \] Dado que: \[ \lim_{\mathit{n} \to \infty} a_{\mathit{n}} = 1 \quad \text{y} \quad \lim_{\mathit{n} \to \infty} b_{\mathit{n}} = -1, \] tenemos: \[ \lim_{\mathit{n} \to \infty} (a_{\mathit{n}} – b_{\mathit{n}}) = 1 – (-1) = 2. \] Paso 3. Sustituimos los resultados en el cociente: \[ \lim_{\mathit{n} \to \infty} \frac{a_{\mathit{n}} + b_{\mathit{n}}}{a_{\mathit{n}} – b_{\mathit{n}}} = \frac{\lim_{\mathit{n} \to \infty} (a_{\mathit{n}} + b_{\mathit{n}})}{\lim_{\mathit{n} \to \infty} (a_{\mathit{n}} – b_{\mathit{n}})} = \frac{0}{2}. \] Por lo tanto: \[ \boxed{\lim_{\mathit{n} \to \infty} \frac{a_{\mathit{n}} + b_{\mathit{n}}}{a_{\mathit{n}} – b_{\mathit{n}}} = 0} \]

29. Encuentre el límite de la siguiente secuencia, usando la regla de L’Hôpital cuando sea apropiado: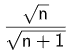

Solución – Juan Beltrán:

Para encontrar el límite de la secuencia \( \frac{\sqrt{\mathit{n}}}{\sqrt{\mathit{n} + 1}} \) cuando \( \mathit{n} \to \infty \), procedemos de la siguiente manera: \[ \] Paso 1. Plantear el límite: \[ \lim_{\mathit{n} \to \infty} \frac{\sqrt{\mathit{n}}}{\sqrt{\mathit{n} + 1}} \] Paso 2. Simplificar la expresión. Dividimos el numerador y denominador entre \( \sqrt{\mathit{n}} \) : \[ \frac{\sqrt{\mathit{n}}}{\sqrt{\mathit{n} + 1}} = \frac{\sqrt{\mathit{n}}}{\sqrt{\mathit{n}} \cdot \sqrt{1 + \frac{1}{\mathit{n}}}} = \frac{1}{\sqrt{1 + \frac{1}{\mathit{n}}}} \] Paso 3. Analizar el límite. Cuando \( \mathit{n} \to \infty \), el término \( \frac{1}{\mathit{n}} \to 0 \), entonces: \[ \sqrt{1 + \frac{1}{\mathit{n}}} \to \sqrt{1} = 1 \] Por lo tanto: \[ \frac{1}{\sqrt{1 + \frac{1}{\mathit{n}}}} \to \frac{1}{1} = 1 \] Paso 4. Solución. El límite de la secuencia es: \[ \boxed{\lim_{\mathit{n} \to \infty} \frac{\sqrt{\mathit{n}}}{\sqrt{\mathit{n} + 1}} = 1} \]

30. Encuentre el límite de la siguiente secuencia, usando la regla de L’Hôpital cuando sea apropiado: n^1/n.

Solución – Juan Beltrán: 

Para encontrar el límite de la secuencia \( \mathit{n}^{\frac{1}{\mathit{n}}} \) cuando \( \mathit{n} \to \infty \), procedemos de la siguiente manera: \[ \] Paso 1. Plantear el límite \[ \lim_{\mathit{n} \to \infty} \mathit{n}^{\frac{1}{\mathit{n}}} \] Paso 2. Aplicar logaritmos. Sea \( a = \mathit{n}^{\frac{1}{\mathit{n}}} \). Tomamos el logaritmo natural: \[ \ln a = \ln \left( \mathit{n}^{\frac{1}{\mathit{n}}} \right) = \frac{1}{\mathit{n}} \ln \mathit{n} \] El límite original se transforma en: \[ \lim_{\mathit{n} \to \infty} \mathit{n}^{\frac{1}{\mathit{n}}} = e^{\lim_{\mathit{n} \to \infty} \frac{\ln \mathit{n}}{\mathit{n}}} \] Paso 3. Evaluar el límite usando la regla de L’Hôpital. Consideramos \( \lim_{\mathit{n} \to \infty} \frac{\ln \mathit{n}}{\mathit{n}} \). Tanto el numerador como el denominador tienden a infinito, por lo que aplicamos la regla de L’Hôpital: \[ \lim_{\mathit{n} \to \infty} \frac{\ln \mathit{n}}{\mathit{n}} = \lim_{\mathit{n} \to \infty} \frac{\frac{d}{d\mathit{n}} (\ln \mathit{n})}{\frac{d}{d\mathit{n}} (\mathit{n})} = \lim_{\mathit{n} \to \infty} \frac{\frac{1}{\mathit{n}}}{1} = \lim_{\mathit{n} \to \infty} \frac{1}{\mathit{n}} = 0 \] Paso 4 Conclusión. Sustituimos este resultado en la expresión exponencial: \[ \lim_{\mathit{n} \to \infty} \mathit{n}^{\frac{1}{\mathit{n}}} = e^0 = 1 \] Por lo tanto, el límite de la secuencia es: \[ \boxed{\lim_{\mathit{n} \to \infty} \mathit{n}^{\frac{1}{\mathit{n}}} = 1} \]

32. Para la secuencia cuyo término enésimo es ln(1 + 1/n) indique si la secuencia está acotada y si eventualmente es monótona, creciente o decreciente.

Solución – Juan Beltrán: 

Analicemos la secuencia \( \{a_n\} \) cuyo término enésimo es: \[ a_n = \ln\left(1 + \frac{1}{n}\right). \] 1. ¿Está acotada? El término general de la secuencia, \( a_n = \ln\left(1 + \frac{1}{n}\right) \), tiene las siguientes propiedades: – Para \( n \geq 1 \), se cumple que \( 1 + \frac{1}{n} > 1 \). Por lo tanto, \( \ln\left(1 + \frac{1}{n}\right) > 0 \). – A medida que \( n \to \infty \), se tiene \( \frac{1}{n} \to 0 \), lo que implica que: \[ \lim_{n \to \infty} a_n = \ln(1) = 0. \] – Para \( n = 1 \), el valor máximo de la secuencia ocurre en el primer término: \[ a_1 = \ln\left(1 + \frac{1}{1}\right) = \ln(2). \] Por lo tanto, la secuencia está acotada en el intervalo: \[ 0 < a_n \leq \ln(2), \quad \forall n \geq 1. \] 2. ¿Es eventualmente monótona, creciente o decreciente? Para determinar la monotonía, calculamos la diferencia \( a_{n+1} - a_n \). Sabemos que: \[ a_{n+1} = \ln\left(1 + \frac{1}{n+1}\right), \quad a_n = \ln\left(1 + \frac{1}{n}\right). \] La diferencia es: \[ a_{n+1} - a_n = \ln\left(1 + \frac{1}{n+1}\right) - \ln\left(1 + \frac{1}{n}\right). \] Usando la propiedad logarítmica \( \ln(x) - \ln(y) = \ln\left(\frac{x}{y}\right) \), obtenemos: \[ a_{n+1} - a_n = \ln\left(\frac{1 + \frac{1}{n+1}}{1 + \frac{1}{n}}\right). \] El cociente \( \frac{1 + \frac{1}{n+1}}{1 + \frac{1}{n}} \) es menor que 1 para \( n \geq 1 \), ya que \( 1 + \frac{1}{n+1} < 1 + \frac{1}{n} \). Por lo tanto: \[ a_{n+1} - a_n < 0, \quad \forall n \geq 1. \] Esto indica que la secuencia es estrictamente decreciente. **Conclusión final:** \[ \boxed{ \text{1. La secuencia está acotada en } 0 < a_n \leq \ln(2). \\ \text{2. La secuencia es estrictamente decreciente para } n \geq 1. } \]