Álgebra lineal con aplicaciones
| 1. Sistema de ecuaciones lineales | Ejercicios propuestos del Capítulo 1.1 |
1.1 Soluciones y operaciones elementales
Los problemas prácticos en muchos campos de estudio, como biología, negocios, química, informática, economía, electrónica, ingeniería, física y ciencias sociales, a menudo pueden reducirse a la resolución de un sistema de ecuaciones lineales. El álgebra lineal surgió de los intentos de encontrar métodos meticulosos para resolver estos sistemas, por lo que es natural comenzar este libro estudiando ecuaciones lineales.
Si a, b y c son números reales, la gráfica de una ecuación de la forma


es una línea recta (si a y b no son ambos cero), por lo que dicha ecuación se llama ecuación lineal en las variables x e y. Sin embargo, a menudo es conveniente escribir las variables como x1, x2, …, xn, particularmente cuando hay más de dos variables involucradas. Una ecuación de la forma.


se llama ecuación lineal en las n variables x1, x2, …, xn. Aquí a1, a2, …, denotan números reales (llamados los coeficientes de x1, x2, …, xn, respectivamente) y b también es un número (llamado término constante de la ecuación). Una colección finita de ecuaciones lineales en las variables x1, x2, …, xn se denomina sistema de ecuaciones lineales en estas variables. Por ejemplo,


es una ecuación lineal; los coeficientes de x1, x2 y x3 son 2, −3 y 5, y el término constante es 7. Tenga en cuenta que cada variable en una ecuación lineal ocurre solo a la primera potencia.
Dada una ecuación lineal a1x1 + a2x2 + ··· + an = b, un conjunto s1, s2, …, sn de n números se llama una solución a la ecuación si


es decir, si la ecuación se satisface cuando se realizan las sustituciones x1 = s1, x2 = s2, …, xn = sn. Un conjunto de números se llama solución a un sistema de ecuaciones si es una solución a cada ecuación en el sistema.
Por ejemplo, x = −2, y = 5, z = 0 y x = 0, y = 4, z = −1 son soluciones para el sistema


Un sistema puede no tener alguna solución, o puede tener una solución única, o puede tener una familia infinita de soluciones Por ejemplo, el sistema x + y = 2, x + y = 3 no tiene solución porque la suma de dos números no puede ser 2 y 3 simultáneamente. Un sistema que no tiene solución se llama inconsistente; un sistema con al menos una solución se llama consistente. El sistema en el siguiente ejemplo tiene infinitas soluciones.
EJEMPLO ILUSTRATIVO 1.1_1
Demuestre que, para valores arbitrarios de s y t


es una solución al sistema


Solución:
Simplemente sustituya estos valores de x1, x2, x3 y x4 en cada ecuación.


Debido a que ambas ecuaciones están satisfechas, es una solución para todas las elecciones de s y t. ◊
Las cantidades s y t del ejemplo 1.1_1 se denominan parámetros y el conjunto de soluciones, que se describe de esta manera, se dice que se da en forma paramétrica y se llama la solución general del sistema.
Resulta que las soluciones a cada sistema de ecuaciones (si hay soluciones) se pueden dar en forma paramétrica (es decir, las variables x1, x2, … se dan en términos de nuevas variables independientes s, t, etc.). El siguiente ejemplo muestra cómo sucede esto en los sistemas más simples donde solo hay una ecuación presente.
EJEMPLO ILUSTRATIVO 1.1_2
Describa todas las soluciones para 3x − y + 2z = 6 en forma paramétrica.
Solución:
Resolviendo la ecuación para y en términos de x y z, obtenemos y = 3x + 2z − 6. Si s y t son arbitrarias, estableciendo x = s, z = t, obtenemos las soluciones


con las variables s y t arbitrarias.
Por supuesto, podríamos haber resuelto x: x = (y − 2z + 6)/3. Entonces, si tomamos y = p, z = q, las soluciones se representan de la siguiente manera:


con las variables p y q arbitrarias.
¡La misma familia de soluciones puede “verse” bastante diferente! ◊


(x = 2, y = 1)




(x = t, y = 3t −4)
Figura 1.1_1
Cuando sólo intervienen dos variables, las soluciones a los sistemas de ecuaciones lineales se pueden describir geométricamente porque la gráfica de una ecuación lineal ax + by = c es una línea recta si a y b no son ambos cero.
Además, un punto P(s, t) con coordenadas s y t se encuentra en la recta si y solo si as + bt = c, es decir, cuando x = s, y = t es una solución a la ecuación. Por lo tanto, las soluciones a un sistema de ecuaciones lineales corresponden a los puntos P(s, t) que se encuentran en todas las rectas en cuestión.
En particular, si el sistema consta de una sola ecuación, debe haber infinitas soluciones porque hay infinitos puntos en una línea recta. Si el sistema tiene dos ecuaciones, hay tres posibilidades para las líneas rectas correspondientes:
1. Las rectas se cruzan en un solo punto. Entonces el sistema tiene una solución única correspondiente a ese punto.
2. Las rectas son paralelas (y distintas) y, por lo tanto, no se cruzan. Entonces el sistema no tiene solución.
3. Las rectas son idénticas. Entonces el sistema tiene infinitas soluciones, una para cada punto en la recta (común).
Estas tres situaciones se ilustran en la figura 1.1_1. En cada caso, se trazan las gráficas de dos rectas específicas y se indican las ecuaciones correspondientes. En el último caso, las ecuaciones son 3x − y = 4 y −6x + 2y = −8, que tienen gráficas idénticas.
Con tres variables, se puede mostrar que la gráfica de una ecuación ax + by + cz = d es un plano (consulte la Sección 4.2) y, por lo tanto, nuevamente proporciona una “imagen” del conjunto de soluciones. Sin embargo, este método gráfico tiene sus limitaciones:
Cuando hay más de tres variables involucradas, no es posible una imagen física de las gráficas (llamadas hiperplanos). Es necesario recurrir a un método de solución más “algebraico”.
Antes de describir el método, presentamos un concepto que simplifica los cálculos involucrados. Considere el siguiente sistema
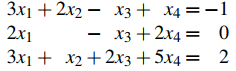
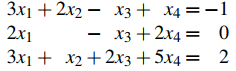
de tres ecuaciones en cuatro variables. El conjunto de números


que ocurre en el sistema se llama matriz aumentada del sistema. Cada fila de la matriz consiste en los coeficientes de las variables (en orden) de la ecuación correspondiente, junto con el término constante. Para mayor claridad, las constantes están separadas por una línea vertical. La matriz aumentada es solo una forma diferente de describir el sistema de ecuaciones. El conjunto de coeficientes de las variables.


se llama matriz de coeficientes del sistema y


se llama la matriz de constantes del sistema.
(Nota: Una arreglo rectangular de números se llama matriz. Las matrices se discutirán con más detalle en el Capítulo 2.)
Operaciones elementales
El método algebraico para resolver sistemas de ecuaciones lineales se describe a continuación. Se dice que dos de estos sistemas son equivalentes si tienen el mismo conjunto de soluciones. Un sistema se resuelve escribiendo una serie de sistemas, uno tras otro, cada uno equivalente al sistema anterior. Cada uno de estos sistemas tiene el mismo conjunto de soluciones que el original; el objetivo es terminar con un sistema que sea fácil de resolver. Cada sistema de la serie se obtiene del sistema anterior mediante una simple manipulación elegida para que no cambie el conjunto de soluciones.
Como ilustración, resolvemos el sistema x + 2y = −2, 2x + y = 7 de esta manera. En cada etapa, se muestra la matriz aumentada correspondiente. El sistema original es


Primero, resta dos veces la primera ecuación de la segunda. El sistema resultante es


que es equivalente al original (ver Teorema 1.1.1). En esta etapa obtenemos y = −11/3 multiplicando la segunda ecuación por −1/3. El resultado es el sistema equivalente


Finalmente, restamos dos veces la segunda ecuación de la primera para obtener otro sistema equivalente


¡Ahora este sistema es fácil de resolver! Y debido a que es equivalente al sistema original, proporciona la solución a ese sistema.
Observe que, en cada etapa, se realiza una determinada operación en el sistema (y, por lo tanto, en la matriz aumentada) para producir un sistema equivalente.
Definición 1.1.1 Operaciones elementales
|
Las siguientes operaciones, llamadas operaciones elementales, pueden realizarse rutinariamente en sistemas de ecuaciones lineales para producir sistemas equivalentes
|
Teorema 1.1.1
| Suponga que se realiza una secuencia de operaciones elementales en un sistema de ecuaciones lineales. Entonces, el sistema resultante tiene el mismo conjunto de soluciones que el original, por lo que los dos sistemas son equivalentes. |
La prueba se da al final de esta sección.
Las operaciones elementales realizadas en un sistema de ecuaciones producen las manipulaciones correspondientes de las filas de la matriz aumentada. Por lo tanto, multiplicar una fila de una matriz por un número k significa multiplicar cada entrada de la fila por k. Agregar una fila a otra fila significa agregar cada entrada de esa fila a la entrada correspondiente de la otra fila. Restar dos filas se hace de manera similar. Tenga en cuenta que consideramos dos filas como iguales cuando las entradas correspondientes son iguales.
En los cálculos manuales (y en programas de computadora) manipulamos las filas de la matriz aumentada en lugar de las ecuaciones. Por esta razón, reformulamos estas operaciones elementales para matrices.
Definición 1.1.2 Operaciones elementales de fila (renglón)
|
Las siguientes se denominan operaciones elementales de fila en una matriz
|
En el ejemplo anterior, una serie de tales operaciones condujo a una matriz de la forma


donde los asteriscos representan números arbitrarios. En el caso de tres ecuaciones en tres variables, el objetivo es producir una matriz de la forma


Esto no siempre sucede, como veremos en la siguiente sección. Aquí hay un ejemplo en el que sucede.
Ejemplo ilustrativo 1.1_3
Encuentre todas las soluciones para el siguiente sistema de ecuaciones.


Solución:
La matriz aumentada del sistema original es


Para crear un 1 en la esquina superior izquierda, podríamos multiplicar la fila 1 por 1/3. Sin embargo, el 1 se puede obtener sin introducir fracciones restando la fila 2 de la fila 1. El resultado es


El 1 de la parte superior izquierda ahora se usa para “limpiar” la primera columna, es decir, crear ceros en las otras posiciones de esa columna. Primero reste 2 veces la fila 1 de la fila 2 para obtener


Luego reste 4 veces la fila 1 de la fila 3. El resultado es


Esto completa el trabajo en la columna 1. Ahora usamos el 1 en la segunda posición de la segunda fila para limpiar la segunda columna restando la fila 2 de la fila 1 y luego sumando la fila 2 a la fila 3.
Por conveniencia, ambas operaciones de fila se realizan en un solo paso. El resultado es
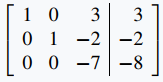
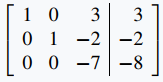
Tenga en cuenta que las dos últimas manipulaciones no afectaron a la primera columna (la segunda fila tiene un cero allí), por lo que nuestro esfuerzo anterior no se ha visto afectado. Finalmente limpiamos la tercera columna. Comience multiplicando la fila 3 por −1/7 para obtener


Ahora resta 3 veces la fila 3 de la fila 1, y luego suma 2 veces la fila 3 a la fila 2 para obtener


Las ecuaciones correspondientes son x = −3/7, y = 2/7, y z = 8/7, que dan la solución (única). ◊
Cada operación elemental de fila puede ser revertida por otra operación de fila elemental del mismo tipo (llamada inversa). Para ver cómo, observemos los tipos I, II y III por separado:
Tipo I Intercambiar dos filas se invierte intercambiándolas nuevamente.
Tipo II Multiplicar una fila por un número distinto de cero k se invierte multiplicando por 1/k
Tipo III Agregar k veces la fila p a una fila diferente q se invierte agregando −k veces la fila p a la fila q (en la nueva matriz). Tenga en cuenta que p ≠ q es esencial aquí.
Para ilustrar la situación de Tipo III, suponga que hay cuatro filas en la matriz original, denotadas R₁, R₂, R₃ y R₄, y que k veces R₂ se agrega a R₃. Luego, la operación inversa agrega −k veces R₂, a R₃. El siguiente diagrama ilustra el efecto de hacer la operación primero y luego a la inversa:


La existencia de inversas para operaciones elementales de fila y, por lo tanto, para operaciones elementales en un sistema de ecuaciones, da los argumentos para la:
| Prueba del teorema 1.1.1 Suponga que un sistema de ecuaciones lineales se transforma en un nuevo sistema mediante una secuencia de operaciones elementales. Entonces, cada solución del sistema original es automáticamente una solución del nuevo sistema porque agregar ecuaciones, o multiplicar una ecuación por un número distinto de cero, siempre da como resultado una ecuación válida. De la misma manera, cada solución del nuevo sistema debe ser una solución para el sistema original porque el sistema original puede obtenerse del nuevo mediante otra serie de operaciones elementales (las inversas de los originales). Se deduce que los sistemas originales y nuevos tienen las mismas soluciones. Esto prueba el teorema 1.1.1. ◊ |
(1.2. Eliminación gaussiana) ⇒
