Álgebra lineal con aplicaciones
| 1. Sistema de ecuaciones lineales | 1.1 Soluciones y operaciones elementales |
Ejercicios propuestos del Capítulo 1.1
1. En cada caso, verifique que las siguientes son soluciones del sistema dado para todos los valores de s y t.
a. x = 19t − 35
y = 25 − 13t
z = t
es una solución de
2x + 3y + z = 5
5x + 7y − 4z = 0
b. x₁ = 2s + 12t + 13
x₂ = s
x₃ = −s − 3t − 3
x₄ = t
es una solución de
2x₁ + 5x₂ + 9x₃ + 3x₄ = −1
x₁ + 2x₂ + 4x₃ = 1
2. Encuentre todas las soluciones a las siguientes ecuaciones y de la respuesta en forma paramétrica de dos maneras distintas.
a. 3x + y = 2
b. 2x + 3y = 1
c. 3x − y + 2z = 5
d. x − 2y + 5z = 1
3. Considerando 2x = 5 como la ecuación 2x + 0y = 5 en dos variables, encuentre todas las soluciones en forma paramétrica.
4. Considerando 4x − 2y = 3 como la ecuación 4x − 2y + 0z = 3 en tres variables, encuentre todas las soluciones en forma paramétrica.
5. Encuentre todas las soluciones para el sistema general ax = b de una ecuación en una variable (a) cuando a = 0 y (b) cuando a ≠ 0.
6. Demuestre que un sistema que consta de exactamente una ecuación lineal puede no tener solución, tener una solución o infinitas soluciones. Dar ejemplos.
7. Escriba la matriz aumentada para cada uno de los siguientes sistemas de ecuaciones lineales.
a. x − 3y = 5
2x + y = 1
b. x + 2y = 0
y = 1
c. x − y + z = 2
x − z = 1
y + 2x = 0
d. x + y = 1
y + z = 0
z − x = 2
8. Escriba un sistema de ecuaciones lineales que tenga cada una de las siguientes matrices aumentadas:
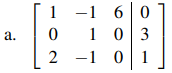
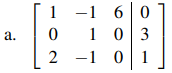


9. Encuentre la solución de cada uno de los siguientes sistemas de ecuaciones lineales usando matrices aumentadas.
a. x − 3y = 1
2x − 7y = 3
b. x + 2y = 1
3x + 4y = −1
c. 2x + 3y = −1
3x + 4y = 2
d. 3x + 4y = 1
4x + 5y = −3
10. Encuentre la solución de cada uno de los siguientes sistemas de ecuaciones lineales usando matrices aumentadas.
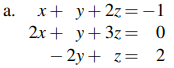
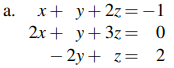


11. Encuentre todas las soluciones (si las hay) de los siguientes sistemas de ecuaciones lineales.
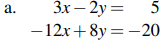
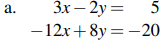


12. Demuestre que el sistema


es inconsistente a menos que c = 2b − 3a.
13. Al examinar las posibles posiciones de las rectas en el plano, demuestre que dos ecuaciones en dos variables pueden tener cero, una o infinitas soluciones.
14. En cada caso, muestre que la afirmación es verdadera o dé un ejemplo que demuestre que es falsa.
- Si un sistema lineal tiene n variables y m ecuaciones,
entonces la matriz aumentada tiene n filas. - Un sistema lineal consistente debe tener infinitamente
muchas soluciones. - Si una operación de fila se realiza a un sistema lineal consistente, el sistema resultante debe ser consistente.
- Si una serie de operaciones de fila en un sistema lineal da como resultado un sistema inconsistente, el sistema original
es inconsistente.
15. Encuentre una expresión cuadrática de la forma cuadrática a + bx + cx² tal que la gráfica de y = a + bx + cx² contenga cada uno de los puntos (−1, 6), (2, 0) y (3, 2).
16. Resuelve el sistema


cambiando variables


y resolver las ecuaciones resultantes para x′ e y′.
17. Encuentre a, b y c tales que


[Sugerencia: Multiplique por (x² + 2)(2x − 1) y equipare los coeficientes de potencias de x.]
18. Un cuidador quiere darle a un animal 42 mg de vitamina A y 65 mg de vitamina D por día. Tiene dos suplementos: el primero contiene 10% de vitamina A y 25% de vitamina D; el segundo contiene 20% de vitamina A y 25% de vitamina D. ¿Cuánto de cada suplemento debe darle al animal cada día?
19. Los trabajadores John y Joe ganan un total de $24,60 cuando John trabaja 2 horas y Joe trabaja 3 horas. Si John trabaja 3 horas y Joe trabaja 2 horas, reciben 23,90 dólares. Encuentre sus respectivas tarifas por hora.
20. Un biólogo quiere crear una dieta a partir de pescado y harina que contenga 183 gramos de proteína y 93 gramos de carbohidratos por día. Si el pescado contiene un 70% de proteínas y un 10% de carbohidratos, y la comida contiene un 30% de proteínas y un 60% de carbohidratos, ¿qué cantidad de cada alimento es requerido cada día?
