ECUACIONES PARAMÉTRICAS Y COORDENADAS POLARES
La elipse
Una elipse también se puede definir en términos de distancias. En el caso de una elipse, hay dos focos (plural de foco) y dos directrices (plural de directriz). Examinamos las directrices con más detalle más adelante en esta sección.
DEFINICIÓN 8.5.2. La Elipse
| Una elipse es el conjunto de todos los puntos para los que la suma de sus distancias desde dos puntos fijos (los focos) es constante. |
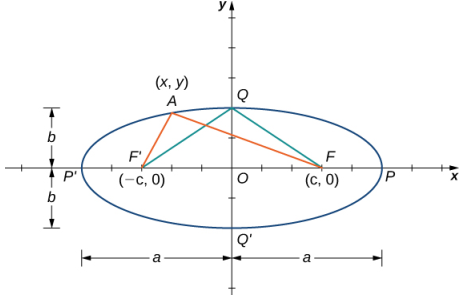
En la figura 8.5_5 se muestra una gráfica de una elipse típica. En esta figura, los focos están etiquetados como F y F′. Ambos están a la misma distancia fija desde el origen, y esta distancia está representada por la variable c. Por lo tanto, las coordenadas de F son (c, 0) y las coordenadas de F′ son (−c, 0). Los puntos P y P′ están ubicados en los extremos del eje mayor de la elipse y tienen coordenadas (a, 0) y (−a, 0), respectivamente. El eje mayor es siempre la distancia más larga a través de la elipse y puede ser horizontal o vertical. Por tanto, la longitud del eje mayor en esta elipse es 2a. Además, P y P′ se denominan vértices de la elipse. Los puntos Q y Q′ están ubicados en los extremos del eje menor de la elipse y tienen coordenadas (0, b) y (0, −b), respectivamente. El eje menor es la distancia más corta a través de la elipse. El eje menor es perpendicular al eje mayor.
Según la definición de la elipse, podemos elegir cualquier punto de la elipse y la suma de las distancias desde este punto a los dos focos es constante. Suponga que elegimos el punto P. Dado que las coordenadas del punto P son (a, 0), la suma de las distancias es
d(P, F) + d(P, F′) = (a − c) + (a + c) = 2a.
Por lo tanto, la suma de las distancias desde un punto arbitrario A con coordenadas (x, y) también es igual a 2a. Usando la fórmula de la distancia, obtenemos


Resta el segundo radical de ambos lados y eleva ambos lados al cuadrado:
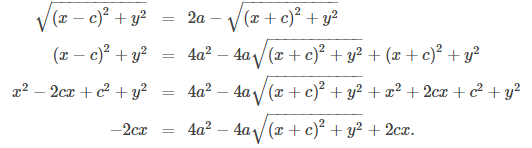
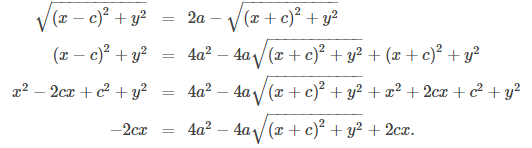
Ahora aísle el radical del lado derecho y vuelva a cuadrarlo:


Aísle las variables del lado izquierdo de la ecuación y las constantes del lado derecho:


Divide ambos lados por a² − c². Esto da la ecuación


Si nos remitimos a la figura 8.5_5, entonces la longitud de cada uno de los dos segmentos de la línea verde es igual a a. Esto es cierto porque la suma de las distancias desde el punto Q a los focos F y F′ es igual a 2a, y las longitudes de estos dos segmentos de recta son iguales. Este segmento de recta forma un triángulo rectángulo con hipotenusa de longitud a y catetos de longitud b y c. Del teorema de Pitágoras, a² = b² + c² y b² = a² − c². Por lo tanto, la ecuación de la elipse se convierte en


Finalmente, si el centro de la elipse se mueve desde el origen a un punto (h, k), tenemos la siguiente forma estándar de una elipse:
TEOREMA 8.5.2. Ecuación de una elipse en forma estándar
|
Considere la elipse con centro (h, k), un eje mayor horizontal con longitud 2a y un eje menor vertical con longitud 2b. Entonces la ecuación de esta elipse en forma estándar es y los focos están ubicados en (h ± c, k), donde c² = a² − b². Las ecuaciones de las directrices son x = h ± a²/c. Si el eje mayor es vertical, entonces la ecuación de la elipse se convierte en y los focos están ubicados en (h, k ± c), donde c² = a² − b². Las ecuaciones de las directrices en este caso son y = k ± a²/c. |
Si el eje mayor es horizontal, entonces la elipse se llama horizontal, y si el eje mayor es vertical, entonces la elipse se llama vertical. La ecuación de una elipse tiene una forma general si tiene la forma Ax² + By² + Cx + Dy + E = 0, donde A y B son ambos positivos o negativos. Para convertir la ecuación de forma general a estándar, use el método de completar el cuadrado.
Ejemplo ilustrativo 8.5_2 Encontrar la forma estándar de una elipse
Pon la ecuación 9x² + 4y² − 36x + 24y + 36 = 0 en forma estándar y grafica la elipse resultante.
Solución:
Primero reste 36 unidades de ambos lados de la ecuación:
9x² + 4y² − 36x + 24y = −36
Luego agrupe los términos x y los términos y juntos, y factorice el factor común:


Necesitamos determinar la constante que, cuando se agrega dentro de cada paréntesis, da como resultado un cuadrado perfecto. En el primer conjunto de paréntesis, toma la mitad del coeficiente de x y eleva al cuadrado. Esto da (−4/2)² = 4. En el segundo conjunto de paréntesis, toma la mitad del coeficiente de y y eleva al cuadrado. Esto da (6/2)² = 9. Agregue estos números dentro de cada par de paréntesis. Dado que el primer conjunto de paréntesis tiene un 9 al frente, en realidad estamos agregando 36 al lado izquierdo. De manera similar, también estamos agregando 36 al segundo conjunto. Por lo tanto, la ecuación se convierte en
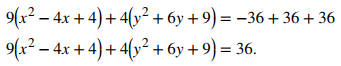
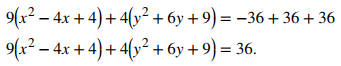
Ahora factorice ambos conjuntos de paréntesis y divídalos por 36:


La ecuación está ahora en forma estándar. Al comparar esto con la ecuación
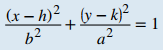
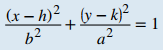
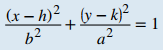
, se obtiene h = 2, k = −3, a = 3 y b = 2. Esta es una elipse vertical con centro en (2, −3), eje mayor 6 y eje menor 4. La gráfica de esta elipse aparece como sigue.


Ejercicio de control 8.5_2
Pon la ecuación 9x² + 16y² + 18x − 64y − 71 = 0 en forma estándar y grafica la elipse resultante.
De acuerdo con la primera ley del movimiento planetario de Kepler, la órbita de un planeta alrededor del Sol es una elipse con el Sol en uno de los focos, como se muestra en la Figura 8.5_7 (a). Debido a que la órbita de la Tierra es una elipse, la distancia del Sol varía a lo largo del año. Un error común es que la Tierra está más cerca del Sol en verano. De hecho, en verano para el hemisferio norte, la Tierra está más lejos del Sol que durante el invierno. La diferencia de estación se debe a la inclinación del eje de la Tierra en el plano orbital. Los cometas que orbitan alrededor del Sol, como el cometa Halley, también tienen órbitas elípticas, al igual que las lunas que orbitan los planetas y los satélites que orbitan la Tierra.
Las elipses también tienen propiedades reflectantes interesantes: un rayo de luz que emana de un foco pasa a través del otro foco después de reflejarse en un espejo en la elipse. Lo mismo ocurre con una onda de sonido. El Salón Nacional de las Estatuas en el Capitolio de los Estados Unidos en Washington, DC, es una sala famosa en forma elíptica, como se muestra en la Figura 8.5_7 (b). Este salón sirvió como lugar de reunión de la Cámara de Representantes de Estados Unidos durante casi cincuenta años. La ubicación de los dos focos de esta sala semielíptica está claramente identificada por marcas en el piso, e incluso si la sala está llena de visitantes, cuando dos personas se paran en estos lugares y se hablan, pueden escucharse mucho entre sí. más claramente de lo que pueden oír a alguien cerca. La leyenda dice que John Quincy Adams tenía su escritorio ubicado en uno de los focos y pudo escuchar a todos los demás en la Casa sin necesidad de pararse. Aunque esto es una buena historia, es poco probable que sea cierto, porque el techo original produjo tantos ecos que hubo que colgar toda la habitación con alfombras para amortiguar el ruido. El techo fue reconstruido en 1902 y solo entonces surgió el ahora famoso efecto de susurro. Otra famosa galería de susurros, el sitio de muchas propuestas de matrimonio, se encuentra en Grand Central Station en la ciudad de Nueva York.
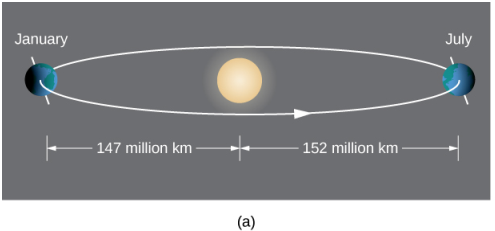



(Figura 8.5_7 (a) La órbita de la Tierra alrededor del Sol es una elipse con el Sol en un foco. (b) Statuary Hall en el Capitolio de los Estados Unidos es una galería susurrante con una sección transversal elíptica.)

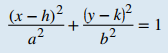
Hola, buenos días,
Excelente sus publicaciones, me han servido muchísimo.
Una pregunta donde encuentro mas sobre la hipérbola o sobre el tema “8.5.3 Identificar la ecuación de una hipérbola en forma estándar con focos dados”
Muchas gracias,
Saludos
Hola Felix.
Gracias por el comentario.
Más tarde, luego de publicar un video que estoy realizando, procederé a publicar sobre lo referente al Capítulo 8.5.3 👀
Saludos! 😺
Ya puede ver los apuntes sobre la hipérbola en https://calculo21.com/secciones-conicas/3/ 👀