| 8.5 Ecuaciones paramétricas y coordenadas polares | Ejercicios propuestos para el Capítulo 8.5 |
8.5 Secciones cónicas
Objetivos de aprendizaje:
8.5.1 Identificar la ecuación de una parábola en forma estándar con un foco y una directriz dados.
8.5.2 Identificar la ecuación de una elipse en forma estándar con focos dados.
8.5.3 Identificar la ecuación de una hipérbola en forma estándar con focos dados.
8.5.4 Reconocer una parábola, elipse o hipérbola a partir de su valor de excentricidad.
8.5.5 Escribir la ecuación polar de una sección cónica con excentricidad e.
8.5.6 Identificar cuándo una ecuación general de grado dos es una parábola, elipse o hipérbola.
Las secciones cónicas se han estudiado desde la época de los antiguos griegos y se consideraban un concepto matemático importante. Ya en el año 320 a. C., matemáticos griegos como Menecmo, Apolonio y Arquímedes estaban fascinados por estas curvas. Apolonio escribió un tratado completo de ocho volúmenes sobre secciones cónicas en el que, por ejemplo, pudo derivar un método específico para identificar una sección cónica mediante el uso de la geometría. Desde entonces, han surgido importantes aplicaciones de las secciones cónicas (por ejemplo, en astronomía), y las propiedades de las secciones cónicas se utilizan en radiotelescopios, receptores de antena parabólica e incluso en arquitectura. En esta sección discutimos las tres secciones cónicas básicas, algunas de sus propiedades y sus ecuaciones.
Las secciones cónicas reciben su nombre porque se pueden generar al interceptar un plano con un cono. Un cono tiene dos partes de forma idéntica llamadas nappes (hojas). La hoja de un cono es lo que la mayoría de la gente quiere decir con “cono”, que tiene la forma de un sombrero de fiesta. Se puede generar un cono circular recto girando una recta que pasa por el origen alrededor del eje y, como se muestra en la siguiente figura.

Las secciones cónicas se generan por la intersección de un plano con un cono (Figura 8.5_2). Si el plano es paralelo al eje de revolución (el eje y), entonces la sección cónica es una hipérbola. Si el plano es paralelo a la recta generadora, la sección cónica es una parábola. Si el plano es perpendicular al eje de revolución, la sección cónica es una circunferencia. Si el plano intersecta una hoja (uno de los conos del doble cono) en ángulo con el eje (que no sea 90°), entonces la sección cónica es una elipse.

Parábolas
Se genera una parábola cuando un plano intersecta un cono paralelo a la recta generadora. En este caso, el plano intersecta solo una de las hojas. Una parábola también se puede definir en términos de distancias.
Definición 8.5.1. La parábola
Una parábola es el conjunto de todos los puntos P(x, y) en el plano que son equidistantes de una recta fija L, llamada directriz y de un punto fijo F, ajeno a la directriz, llamado foco. ♦
- El vértice de la parábola es el punto medio entre el foco y la directriz.
- El eje de la parábola es la recta que pasa por el foco y el vértice.
- La parábola es simétrica respecto de su eje.
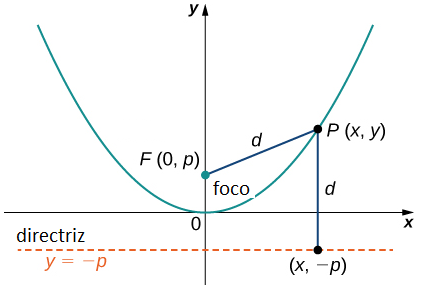
La gráfica de una parábola típica aparece en la figura 8.5_3. Usando este diagrama junto con la fórmula de la distancia, podemos deducir una ecuación para la parábola. Recordemos la fórmula de la distancia: dado el punto P con coordenadas (x₁, y₁) y el punto Q con coordenadas (x₂, y₂), la distancia entre ellos viene dada por la fórmula
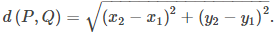
Luego, a partir de la definición de parábola y la Figura 8.5_3, obtenemos

Al cuadrar ambos miembros de la igualdad y simplificando, se obtiene
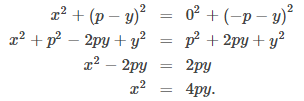
Ahora supongamos que queremos reubicar el vértice. Usamos las variables (h, k) para denotar las coordenadas del vértice. Entonces, si el foco está directamente sobre el vértice, tiene coordenadas (h, k + p) y la directriz tiene la ecuación y = k − p. De manera similar a como se dedujo la ecuación para el vértice en el origen se obtiene la fórmula (x − h)² = 4p (y − k). Resolver esta ecuación para y lleva al siguiente teorema.
TEOREMA 8.5.1. Ecuaciones para parábolas
Dada una parábola que se abre hacia arriba con vértice ubicado en \((h, k)\) y foco ubicado en \((h, k+p)\), donde \(p\) es una constante, la ecuación para la parábola está dada por
\[y = \frac{1}{4p}(x-h)^2 + k.\]
Esta es la forma estándar de una parábola. ♦
También podemos estudiar los casos en que la parábola abre hacia abajo o hacia la izquierda o hacia la derecha. La ecuación para cada uno de estos casos también se puede escribir en forma estándar como se muestra en las siguientes gráficas:
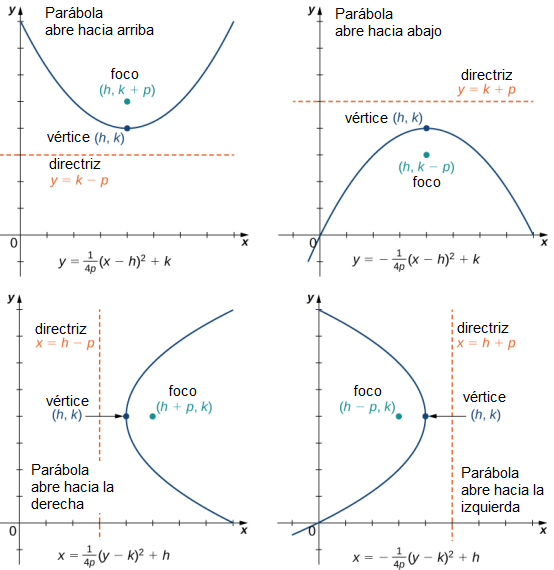
Además, la ecuación de una parábola se puede escribir en forma general, aunque en esta forma los valores de h, k y p no son reconocibles de inmediato. La forma general de una parábola se escribe como

La primera ecuación representa una parábola que abre hacia arriba o hacia abajo. La segunda ecuación representa una parábola que abre hacia la izquierda o hacia la derecha. Para poner la ecuación en forma estándar, use el método de completar el cuadrado.
Ejemplo ilustrativo 8.5_1 Conversión de la ecuación de una parábola de forma general a estándar
Escriba la ecuación 2y² − x + 12y + 16 = 0 en forma estándar y grafique la parábola resultante.
Solución:
Dado que y no se eleva al cuadrado en esta ecuación, sabemos que la parábola abre hacia arriba o hacia abajo. Por lo tanto, necesitamos resolver esta ecuación para y, lo que pondrá la ecuación en forma estándar. Para hacer eso, primero agregue 8y a ambos lados de la ecuación:
8y = x² − 4x + 12.
El siguiente paso es completar el cuadrado del lado derecho. Comience agrupando los dos primeros términos del lado derecho usando paréntesis:
8y = (x² − 4x) + 12.
A continuación, determine la constante que, cuando se agrega entre paréntesis, hace que la cantidad entre paréntesis sea un trinomio cuadrado perfecto. Para hacer esto, toma la mitad del coeficiente de x y eleva al cuadrado. Esto da (−4/2)² = 4. Sume 4 dentro del paréntesis y reste 4 fuera del paréntesis, para que el valor de la ecuación no cambie:
8y = (x² − 4x + 4) + 12 − 4.
Ahora combine los términos semejantes y factorice la cantidad entre paréntesis:
8y = (x − 2)² + 8.
Finalmente, divide por 8:
y = (1/8)(x − 2)² + 1.
Esta ecuación está ahora en forma estándar. Al comparar esto con la ecuación

se obtiene h = 2, k = 1 y p = 2. La parábola abre hacia arriba, con vértice en (2, 1), foco en (2, 3) y directriz y = −1. El gráfico de esta parábola aparece a continuación.

Ejercicio de control 8.5_1
Pon la ecuación 2y² − x + 12y + 16 = 0 en forma estándar y grafica la parábola resultante. ♦
El eje de simetría de una parábola vertical (que abra hacia arriba o hacia abajo) es una recta vertical que pasa por el vértice. La parábola tiene una propiedad reflexiva interesante. Supongamos que tenemos una antena parabólica con una sección transversal parabólica. Si un haz de ondas electromagnéticas, como la luz o las ondas de radio, ingresa al plato en línea recta desde un satélite (paralelo al eje de simetría), entonces las ondas se reflejan en el plato y se acumulan en el foco de la parábola como se muestra en la siguiente figura.

Considere un plato parabólico diseñado para recoger señales de un satélite en el espacio. El plato está dirigido directamente al satélite, y un receptor está ubicado en el foco de la parábola. Las ondas de radio procedentes del satélite se reflejan desde la superficie de la parábola hasta el receptor, que recoge y decodifica las señales digitales. Esto permite que un receptor pequeño recopile señales desde un gran ángulo de cielo. Las linternas y los faros de un automóvil funcionan con el mismo principio, pero a la inversa: la fuente de la luz (es decir, la bombilla) se encuentra en el foco y la superficie reflectante en el espejo parabólico enfoca el haz en línea recta. Esto permite que una pequeña bombilla ilumine un amplio ángulo de espacio frente a la linterna o el automóvil.
La elipse
Una elipse también se puede definir en términos de distancias. En el caso de una elipse, hay dos focos (plural de foco) y dos directrices (plural de directriz). Examinamos las directrices con más detalle más adelante en esta sección.
DEFINICIÓN 8.5.2. La Elipse
Una elipse es el conjunto de todos los puntos para los que la suma de sus distancias desde dos puntos fijos (los focos) es constante. ♦
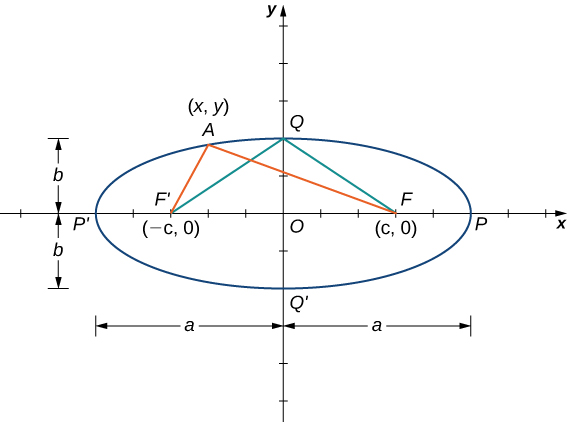
Figura 8.5_5 Una elipse típica en la que la suma de las distancias desde cualquier punto de la elipse a los focos es constante.
En la figura 8.5_5 se muestra una gráfica de una elipse típica. En esta figura, los focos están etiquetados como F y F′. Ambos están a la misma distancia fija desde el origen, y esta distancia está representada por la variable c. Por lo tanto, las coordenadas de F son (c, 0) y las coordenadas de F′ son (−c, 0). Los puntos P y P′ están ubicados en los extremos del eje mayor de la elipse y tienen coordenadas (a, 0) y (−a, 0), respectivamente. El eje mayor es siempre la distancia más larga a través de la elipse y puede ser horizontal o vertical. Por tanto, la longitud del eje mayor en esta elipse es 2a. Además, P y P′ se denominan vértices de la elipse. Los puntos Q y Q′ están ubicados en los extremos del eje menor de la elipse y tienen coordenadas (0, b) y (0, −b), respectivamente. El eje menor es la distancia más corta a través de la elipse. El eje menor es perpendicular al eje mayor.
Según la definición de la elipse, podemos elegir cualquier punto de la elipse y la suma de las distancias desde este punto a los dos focos es constante. Suponga que elegimos el punto P. Dado que las coordenadas del punto P son (a, 0), la suma de las distancias es
d(P, F) + d(P, F′) = (a − c) + (a + c) = 2a.
Por lo tanto, la suma de las distancias desde un punto arbitrario A con coordenadas (x, y) también es igual a 2a. Usando la fórmula de la distancia, obtenemos

Resta el segundo radical de ambos lados y eleva ambos lados al cuadrado:
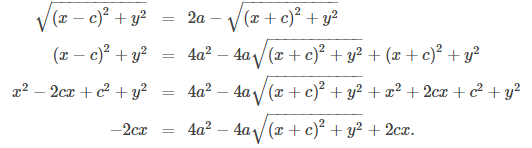
Ahora aísle el radical del lado derecho y vuelva a cuadrarlo:

Aísle las variables del lado izquierdo de la ecuación y las constantes del lado derecho:

Divide ambos lados por a² − c². Esto da la ecuación

Si nos remitimos a la figura 8.5_5, entonces la longitud de cada uno de los dos segmentos de la línea verde es igual a a. Esto es cierto porque la suma de las distancias desde el punto Q a los focos F y F′ es igual a 2a, y las longitudes de estos dos segmentos de recta son iguales. Este segmento de recta forma un triángulo rectángulo con hipotenusa de longitud a y catetos de longitud b y c. Del teorema de Pitágoras, a² = b² + c² y b² = a² − c². Por lo tanto, la ecuación de la elipse se convierte en

Finalmente, si el centro de la elipse se mueve desde el origen a un punto (h, k), tenemos la siguiente forma estándar de una elipse:
TEOREMA 8.5.2. Ecuación de una elipse en forma estándar
Considera la elipse con centro \( (h, k) \), un eje mayor horizontal con longitud \( 2a \) y un eje menor vertical con longitud \( 2b \). Entonces, la ecuación de esta elipse en forma estándar es
\[ \frac{(x – h)^2}{a^2} + \frac{(y – k)^2}{b^2} = 1 \]y los focos se ubican en \( (h \pm c, k) \), donde \( c^2 = a^2 – b^2 \). Las ecuaciones de las directrices son \( x = h \pm \frac{a^2}{c} \).
Si el eje mayor es vertical, entonces la ecuación de la elipse se convierte en
\[ \frac{(x – h)^2}{b^2} + \frac{(y – k)^2}{a^2} = 1 \]y los focos se ubican en \( (h, k \pm c) \), donde \( c^2 = a^2 – b^2 \). Las ecuaciones de las directrices en este caso son \( y = k \pm \frac{a^2}{c} \).
♦
Si el eje mayor es horizontal, entonces la elipse se llama horizontal, y si el eje mayor es vertical, entonces la elipse se llama vertical. La ecuación de una elipse tiene una forma general si tiene la forma Ax² + By² + Cx + Dy + E = 0, donde A y B son ambos positivos o negativos. Para convertir la ecuación de forma general a estándar, use el método de completar el cuadrado.
Ejemplo ilustrativo 8.5_2 Encontrar la forma estándar de una elipse
Pon la ecuación 9x² + 4y² − 36x + 24y + 36 = 0 en forma estándar y grafica la elipse resultante.
Solución:
Primero reste 36 unidades de ambos lados de la ecuación:
9x² + 4y² − 36x + 24y = −36
Luego agrupe los términos x y los términos y juntos, y factorice el factor común:

Necesitamos determinar la constante que, cuando se agrega dentro de cada paréntesis, da como resultado un cuadrado perfecto. En el primer conjunto de paréntesis, toma la mitad del coeficiente de x y eleva al cuadrado. Esto da (−4/2)² = 4. En el segundo conjunto de paréntesis, toma la mitad del coeficiente de y y eleva al cuadrado. Esto da (6/2)² = 9. Agregue estos números dentro de cada par de paréntesis. Dado que el primer conjunto de paréntesis tiene un 9 al frente, en realidad estamos agregando 36 al lado izquierdo. De manera similar, también estamos agregando 36 al segundo conjunto. Por lo tanto, la ecuación se convierte en
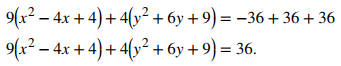
Ahora factorice ambos conjuntos de paréntesis y divídalos por 36:

La ecuación está ahora en forma estándar. Al comparar esto con la ecuación
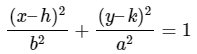
, se obtiene h = 2, k = −3, a = 3 y b = 2. Esta es una elipse vertical con centro en (2, −3), eje mayor 6 y eje menor 4. La gráfica de esta elipse aparece como sigue.
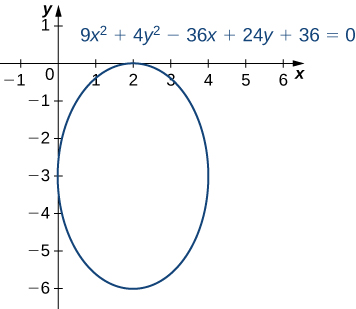
Figura 8.5_6 La elipse para este ejercicio
Ejercicio de control 8.5_2
Pon la ecuación 9x² + 16y² + 18x − 64y − 71 = 0 en forma estándar y grafica la elipse resultante. ♦
De acuerdo con la primera ley del movimiento planetario de Kepler, la órbita de un planeta alrededor del Sol es una elipse con el Sol en uno de los focos, como se muestra en la Figura 8.5_7 (a). Debido a que la órbita de la Tierra es una elipse, la distancia del Sol varía a lo largo del año. Un error común es que la Tierra está más cerca del Sol en verano. De hecho, en verano para el hemisferio norte, la Tierra está más lejos del Sol que durante el invierno. La diferencia de estación se debe a la inclinación del eje de la Tierra en el plano orbital. Los cometas que orbitan alrededor del Sol, como el cometa Halley, también tienen órbitas elípticas, al igual que las lunas que orbitan los planetas y los satélites que orbitan la Tierra.
Las elipses también tienen propiedades reflectantes interesantes: un rayo de luz que emana de un foco pasa a través del otro foco después de reflejarse en un espejo en la elipse. Lo mismo ocurre con una onda de sonido. El Salón Nacional de las Estatuas en el Capitolio de los Estados Unidos en Washington, DC, es una sala famosa en forma elíptica, como se muestra en la Figura 8.5_7 (b). Este salón sirvió como lugar de reunión de la Cámara de Representantes de Estados Unidos durante casi cincuenta años. La ubicación de los dos focos de esta sala semielíptica está claramente identificada por marcas en el piso, e incluso si la sala está llena de visitantes, cuando dos personas se paran en estos lugares y se hablan, pueden escucharse mucho entre sí. más claramente de lo que pueden oír a alguien cerca. La leyenda dice que John Quincy Adams tenía su escritorio ubicado en uno de los focos y pudo escuchar a todos los demás en la Casa sin necesidad de pararse. Aunque esto es una buena historia, es poco probable que sea cierto, porque el techo original produjo tantos ecos que hubo que colgar toda la habitación con alfombras para amortiguar el ruido. El techo fue reconstruido en 1902 y solo entonces surgió el ahora famoso efecto de susurro. Otra famosa galería de susurros, el sitio de muchas propuestas de matrimonio, se encuentra en Grand Central Station en la ciudad de Nueva York.
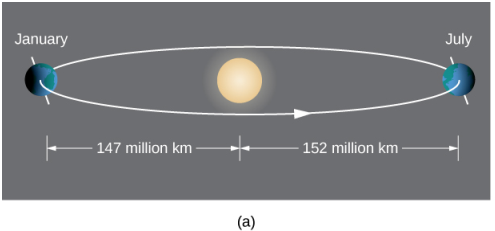

(Figura 8.5_7 (a) La órbita de la Tierra alrededor del Sol es una elipse con el Sol en un foco. (b) Statuary Hall en el Capitolio de los Estados Unidos es una galería susurrante con una sección transversal elíptica.)
La hipérbola
Una hipérbola también se puede definir en términos de distancias. En el caso de una hipérbola, hay dos focos y dos directrices. Las hipérbolas también tienen dos asíntotas.
DEFINICIÓN 8.5.3. La hipérbola
Una hipérbola es el conjunto de todos los puntos donde la diferencia entre sus distancias desde dos puntos fijos (los focos) es constante. ♦
Una gráfica de una hipérbola típica aparece como sigue.

La deducción de la ecuación de una hipérbola en forma estándar es prácticamente idéntica a la de una elipse. Hay un pequeño inconveniente en la definición: la diferencia entre dos números es siempre positiva. Sea P un punto de la hipérbola con coordenadas (x, y). Entonces, la definición de la hipérbola da |d(P, F₁) − d(P, F₂)| = constante. Para simplificar la deducción, suponga que P está en la rama derecha de la hipérbola, por lo que las barras de valor absoluto se obvian. Si está en la rama izquierda, entonces la resta se invierte. El vértice de la rama derecha tiene coordenadas (a, 0), entonces

Por tanto, esta ecuación es cierta para cualquier punto de la hipérbola. Volviendo a las coordenadas (x, y) para P:

Sumando el segundo radical de ambos lados y elevando ambos lados al cuadrado, se obtiene:

Ahora aísle el radical del lado derecho y vuelva a cuadrarlo, para obtener:

Aísle las variables del lado izquierdo de la ecuación y las constantes del lado derecho:

Finalmente, divida ambos lados por a² − c². Esto proporciona la ecuación:

Ahora definimos b de modo que b² =a² − c². Esto es posible porque c > a. Por lo tanto, la ecuación de la hipérbola se convierte en

Finalmente, si el centro de la hipérbola se mueve desde el origen al punto (h, k), tenemos la siguiente forma estándar de la hipérbola:
TEOREMA 8.5.3: Ecuación de una hipérbola en forma estándar
Considera la hipérbola con centro \( (h, k) \), un eje mayor horizontal y un eje menor vertical. Entonces, la ecuación de esta hipérbola es
\[ \frac{(x – h)^2}{a^2} – \frac{(y – k)^2}{b^2} = 1 \]y los focos se ubican en \( (h \pm c, k) \), donde \( c^2 = a^2 + b^2 \). Las ecuaciones de las asíntotas están dadas por \( y = k \pm \frac{b}{a}(x – h) \). Las ecuaciones de las directrices son
\[ x = h \pm \frac{a^2}{\sqrt{a^2 + b^2}} = h \pm \frac{a^2}{c}. \]Si el eje mayor es vertical, entonces la ecuación de la hipérbola se convierte en
\[ \frac{(y – k)^2}{a^2} – \frac{(x – h)^2}{b^2} = 1 \]y los focos se ubican en \( (h, k \pm c) \), donde \( c^2 = a^2 + b^2 \). Las ecuaciones de las asíntotas están dadas por \( y = k \pm \frac{a}{b}(x – h) \). Las ecuaciones de las directrices son
\[ y = k \pm \frac{a^2}{\sqrt{a^2 + b^2}} = k \pm \frac{a^2}{c}. \]♦
Si el eje mayor (eje transversal) es horizontal, entonces la hipérbola se llama horizontal, y si el eje mayor es vertical, la hipérbola se denomina vertical. La ecuación de una hipérbola tiene una forma general si tiene la forma Ax² + By² + Cx + Dy + E = 0, donde A y B tienen signos opuestos. Para convertir la ecuación de forma general a estándar, use el método de completar el cuadrado.
Ejemplo ilustrativo 8.5_3. Encontrar la forma estándar de una hipérbola
Ponga la ecuación 9x² −16y² + 36x + 32y − 124 = 0 en forma estándar y grafique la hipérbola resultante. ¿Cuáles son las ecuaciones de las asíntotas?
Solución:
Primero sume 124 unidades en ambos lados de la ecuación:
9x² −16y² + 36x + 32y = 124.
A continuación, agrupe los términos x y los términos y juntos, luego factorice los factores comunes:

Necesitamos determinar la constante que, cuando se agrega dentro de cada paréntesis, da como resultado un cuadrado perfecto. En el primer conjunto de paréntesis, toma la mitad del coeficiente de x y eleva al cuadrado. Esto da (4/2)² = 4. En el segundo conjunto de paréntesis, toma la mitad del coeficiente de y y eleva al cuadrado. Esto da (−2/2)² = 1. Agregue estos números dentro de cada par de paréntesis. Dado que el primer conjunto de paréntesis tiene un 9 al frente, en realidad estamos agregando 36 al lado izquierdo. De manera similar, restamos 16 del segundo par de paréntesis. Por lo tanto, la ecuación se convierte en

A continuación, factorice ambos conjuntos de paréntesis y divídalos por 144:

La ecuación está ahora en forma estándar. Al comparar esto con la ecuación
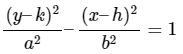
, se obtiene h = −2, k = 1, a = 4 y b = 3. Ésta es una hipérbola horizontal con centro en (−2, 1) y asíntotas dadas por las ecuaciones y = 1 ± (3/4)(x + 2). La gráfica de esta hipérbola aparece en la siguiente figura.

Ejercicio de control 8.5_3
Ponga la ecuación 4y² − 9x² + 16y + 18x − 29 = 0 en forma estándar y grafique la hipérbola resultante. ¿Cuáles son las ecuaciones de las asíntotas? ♦
Las hipérbolas también tienen interesantes propiedades reflectantes. Un rayo dirigido hacia un foco de una hipérbola es reflejado por un espejo hiperbólico hacia el otro foco. Este concepto se ilustra en la siguiente figura.

Esta propiedad de la hipérbola tiene importantes aplicaciones. Se utiliza en radiogoniometría (ya que la diferencia de señales de dos torres es constante a lo largo de hipérbolas) y en la construcción de espejos dentro de telescopios (para reflejar la luz procedente del espejo parabólico al ocular). Otro hecho interesante sobre las hipérbolas es que para un cometa que ingresa al sistema solar, si la velocidad es lo suficientemente grande como para escapar de la atracción gravitacional del Sol, entonces el camino que toma el cometa al pasar a través del sistema solar es hiperbólico.
Excentricidad y Directriz
Una forma alternativa de describir una sección cónica involucra las directrices, los focos y una nueva propiedad llamada excentricidad. Veremos que el valor de la excentricidad de una sección cónica puede definir de forma única a esa cónica.
Definición 8.5.4
La excentricidad \( e \) de una sección cónica se define como la distancia desde cualquier punto en la sección cónica hasta su foco, dividida por la distancia perpendicular desde ese punto hasta la directriz más cercana. Este valor es constante para cualquier sección cónica y también puede definir la sección cónica:
- Si \( e = 1 \), la cónica es una parábola.
- Si \( e < 1 \), es una elipse.
- Si \( e > 1 \), es una hipérbola.
La excentricidad de un círculo es cero. La directriz de una sección cónica es la línea que, junto con el punto conocido como el foco, sirve para definir una sección cónica. Las hipérbolas y las elipses no circulares tienen dos focos y dos directrices asociadas. Las parábolas tienen un foco y una directriz. ♦
Las tres secciones cónicas con sus directrices aparecen en la siguiente figura.
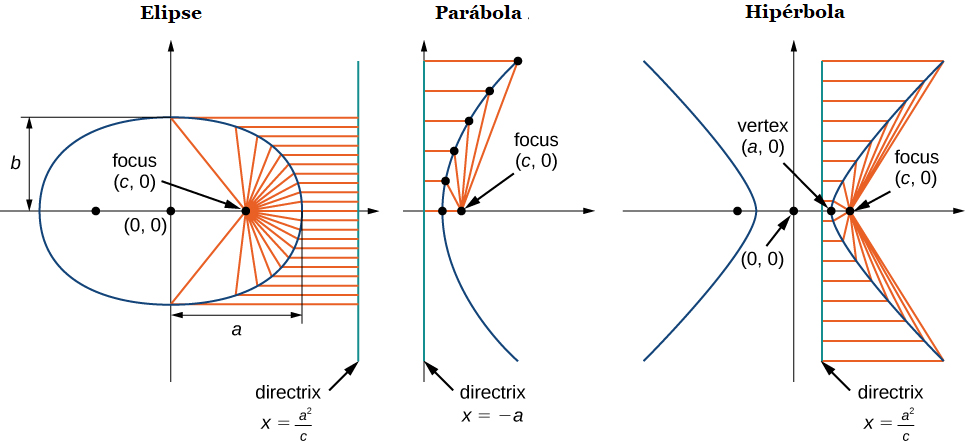
Figura 8.5.11 Las tres secciones cónicas con sus focos y directrices.
Recuerda de la definición de una parábola que la distancia desde cualquier punto en la parábola al foco es igual a la distancia desde ese mismo punto a la directriz. Por lo tanto, por definición, la excentricidad de una parábola debe ser 1. Las ecuaciones de las directrices de una elipse horizontal son \( x = \pm \frac{a^2}{c} \). El vértice derecho de la elipse se ubica en \( (a, 0) \) y el foco derecho está en \( (c, 0) \). Por lo tanto, la distancia desde el vértice hasta el foco es \( a – c \) y la distancia desde el vértice hasta la directriz derecha es \( \frac{a^2}{c} – a \). Esto da la excentricidad como
\[ e = \frac{a – c}{\frac{a^2}{c} – a} = \frac{c(a – c)}{a^2 – ac} = \frac{c(a – c)}{a(a – c)} = \frac{c}{a}. \]Dado que \( c < a \), este paso prueba que la excentricidad de una elipse es menor que 1. Las directrices de una hipérbola horizontal también se ubican en \( x = \pm \frac{a^2}{c} \), y un cálculo similar muestra que la excentricidad de una hipérbola también es \( e = \frac{c}{a} \). Sin embargo, en este caso tenemos \( c > a \), por lo que la excentricidad de una hipérbola es mayor que 1.
Ejemplo ilustrativo 8.5.4: Determinación de la Excentricidad de una Sección Cónica
Determina la excentricidad de la elipse descrita por la ecuación
\[ \frac{(x – 3)^2}{16} + \frac{(y + 2)^2}{25} = 1. \]Solución:
De la ecuación vemos que \( a = 5 \) y \( b = 4 \). El valor de \( c \) se puede calcular usando la ecuación \( a^2 = b^2 + c^2 \) para una elipse. Sustituyendo los valores de \( a \) y \( b \) y resolviendo para \( c \) obtenemos \( c = 3 \).
Por lo tanto, la excentricidad de la elipse es \( e = \frac{c}{a} = \frac{3}{5} = 0.6 \).
♦
Ejercicio de control 8.5_4
Determina la excentricidad de la hipérbola descrita por la ecuación
\[ \frac{(y – 3)^2}{49} – \frac{(x + 2)^2}{25} = 1. \]♦
Ecuaciones Polares de las Secciones Cónicas
A veces es útil escribir o identificar la ecuación de una sección cónica en forma polar. Para ello, necesitamos el concepto de parámetro focal. El parámetro focal p de una sección cónica se define como la distancia desde un foco a la directriz más cercana. La siguiente tabla proporciona los parámetros focales para los diferentes tipos de cónicas, donde a es la longitud del semieje mayor (es decir, la mitad de la longitud del eje mayor), c es la distancia desde el origen al foco y e es la excentricidad. En el caso de una parábola, a representa la distancia desde el vértice al foco.
| Cónica | \( e \) | \( p \) |
|---|---|---|
| Elipse | \( 0 < e < 1 \) | \( \frac{a^2 – c^2}{c} = \frac{a(1 – e^2)}{e} \) |
| Parábola | \( e = 1 \) | \( 2a \) |
| Hipérbola | \( e > 1 \) | \( \frac{c^2 – a^2}{c} = \frac{a(e^2 – 1)}{e} \) |
Tabla 8.5.1 Excentricidades y Parámetros Focales de las Secciones Cónicas
Usando las definiciones del parámetro focal y la excentricidad de la sección cónica, podemos derivar una ecuación para cualquier sección cónica en coordenadas polares. En particular, asumimos que uno de los focos de una sección cónica dada se encuentra en el polo. Entonces, usando la definición de las diversas secciones cónicas en términos de distancias, es posible probar el siguiente teorema.
TEOREMA 8.5.4: Ecuación Polar de las Secciones Cónicas
La ecuación polar de una sección cónica con parámetro focal \( p \) está dada por
\[ r = \frac{ep}{1 \pm e \cos \theta} \quad \text{o} \quad r = \frac{ep}{1 \pm e \sin \theta}. \]♦
En la ecuación de la izquierda, el eje mayor de la sección cónica es horizontal, y en la ecuación de la derecha, el eje mayor es vertical. Para trabajar con una sección cónica escrita en forma polar, primero se hace que el término constante en el denominador sea igual a 1. Esto se puede hacer dividiendo tanto el numerador como el denominador de la fracción por la constante que aparece delante del signo más o menos en el denominador. Entonces, el coeficiente del seno o coseno en el denominador es la excentricidad. Este valor identifica la cónica. Si aparece el coseno en el denominador, entonces la cónica es horizontal. Si aparece el seno, entonces la cónica es vertical. Si aparecen ambos, entonces los ejes están rotados. El centro de la cónica no está necesariamente en el origen. El centro está en el origen solo si la cónica es una circunferencia (es decir, e = 0).
Ejemplo ilustrativo 8.5.5: Graficando una Sección Cónica en Coordenadas Polares
Identifica y crea una gráfica de la sección cónica descrita por la ecuación
\[ r = \frac{3}{1 + 2 \cos \theta}. \]Solución:
El término constante en el denominador es 1, por lo que la excentricidad de la cónica es 2. Esta es una hipérbola. El parámetro focal \( p \) se puede calcular usando la ecuación \( ep = 3 \). Dado que \( e = 2 \), esto da \( p = \frac{3}{2} \). La función coseno aparece en el denominador, por lo que la hipérbola es horizontal. Elige algunos valores para \( \theta \) y crea una tabla de valores. Luego podemos graficar la hipérbola (Figura 8.5.12).
| \( \theta \) | \( r \) | \( \theta \) | \( r \) |
|---|---|---|---|
| \( 0 \) | \( 1 \) | \( \pi \) | \( -3 \) |
| \( \frac{\pi}{4} \) | \( \frac{3}{1 + \sqrt{2}} \approx 1.2426 \) | \( \frac{5\pi}{4} \) | \( \frac{3}{1 – \sqrt{2}} \approx -7.2426 \) |
| \( \frac{\pi}{2} \) | \( 3 \) | \( \frac{3\pi}{2} \) | \( 3 \) |
| \( \frac{3\pi}{4} \) | \( \frac{3}{1 – \sqrt{2}} \approx -7.2426 \) | \( \frac{7\pi}{4} \) | \( \frac{3}{1 + \sqrt{2}} \approx 1.2426 \) |
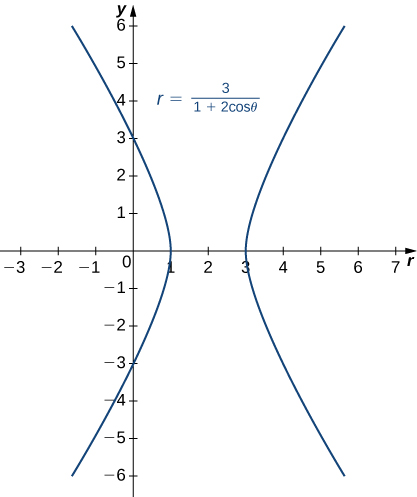
Figura 8.5.12 Gráfica de la hipérbola descrita en este Ejemplo. ♦
Ejercicio de control 8.5_5
Identifica y crea una gráfica de la sección cónica descrita por la ecuación
\[ r = \frac{4}{1 – 0.8 \sin \theta}. \]♦
Ecuaciones Generales de Segundo Grado
Una ecuación general de grado dos se puede escribir en la forma
\[ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0. \]La gráfica de una ecuación de esta forma es una sección cónica. Si \( B \neq 0 \) entonces los ejes de coordenadas se rotan. Para identificar la sección cónica, usamos el discriminante de la sección cónica \( 4AC – B^2 \). Uno de los siguientes casos debe ser verdadero:
- \( 4AC – B^2 > 0 \). Si es así, la gráfica es una elipse.
- \( 4AC – B^2 = 0 \). Si es así, la gráfica es una parábola.
- \( 4AC – B^2 < 0 \). Si es así, la gráfica es una hipérbola.
El ejemplo más simple de una ecuación de segundo grado que involucra un término cruzado es \( xy = 1 \). Esta ecuación se puede resolver para \( y \) para obtener \( y = \frac{1}{x} \). La gráfica de esta función se llama hipérbola rectangular como se muestra.
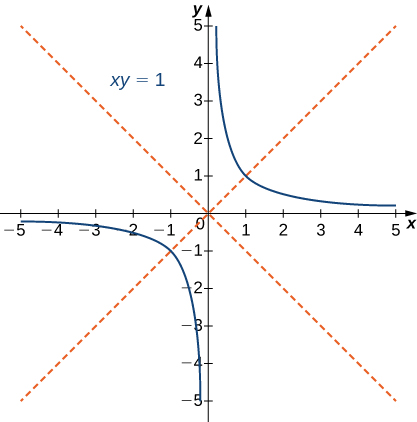
Figura 8.5.13 Gráfica de la ecuación xy = 1; las líneas rojas indican los ejes rotados.
Las asíntotas de esta hipérbola son los ejes x e y. Para determinar el ángulo \( \theta \) de rotación de la sección cónica, usamos la fórmula \( \cot 2\theta = \frac{A – C}{B} \). En este caso \( A = C = 0 \) y \( B = 1 \), por lo que \( \cot 2\theta = (0 – 0) / 1 = 0 \) y \( \theta = 45^\circ \). El método para graficar una sección cónica con ejes rotados implica determinar los coeficientes de la cónica en el sistema de coordenadas rotado. Los nuevos coeficientes se etiquetan como \( A’ \), \( B’ \), \( C’ \), \( D’ \), \( E’ \) y \( F’ \) y están dados por las fórmulas
\[ \begin{aligned} A’ &= A \cos^2 \theta + B \cos \theta \sin \theta + C \sin^2 \theta \\ B’ &= 0 \\ C’ &= A \sin^2 \theta – B \sin \theta \cos \theta + C \cos^2 \theta \\ D’ &= D \cos \theta + E \sin \theta \\ E’ &= -D \sin \theta + E \cos \theta \\ F’ &= F. \end{aligned} \]El procedimiento para graficar una cónica rotada es el siguiente:
- Identifica la sección cónica usando el discriminante \( 4AC – B^2 \).
- Determina \( \theta \) usando la fórmula \( \cot 2\theta = \frac{A – C}{B} \).
- Calcula \( A’ \), \( B’ \), \( C’ \), \( D’ \), \( E’ \) y \( F’ \).
- Reescribe la ecuación original usando \( A’ \), \( B’ \), \( C’ \), \( D’ \), \( E’ \) y \( F’ \).
- Dibuja una gráfica usando la ecuación rotada.
Ejemplo ilustrativo 8.5.6: Identificando una Cónica Rotada
Identifica la cónica y calcula el ángulo de rotación de los ejes para la curva descrita por la ecuación
\[ 13x^2 – 6\sqrt{3}xy + 7y^2 – 256 = 0. \]Solución:
En esta ecuación, \( A = 13 \), \( B = -6\sqrt{3} \), \( C = 7 \), \( D = 0 \), \( E = 0 \) y \( F = -256 \). El discriminante de esta ecuación es \( 4AC – B^2 = 4(13)(7) – (-6\sqrt{3})^2 = 364 – 108 = 256 \). Por lo tanto, esta cónica es una elipse. Para calcular el ángulo de rotación de los ejes, usa \( \cot 2\theta = \frac{A – C}{B} \). Esto da
\[ \cot 2\theta = \frac{A – C}{B} = \frac{13 – 7}{-6\sqrt{3}} = -\frac{\sqrt{3}}{3}. \]Por lo tanto, \( 2\theta = 120^\circ \) y \( \theta = 60^\circ \), que es el ángulo de rotación de los ejes. Para determinar los coeficientes rotados, usa las fórmulas dadas anteriormente:
\[ \begin{aligned} A’ &= A \cos^2 \theta + B \cos \theta \sin \theta + C \sin^2 \theta \\ &= 13 \cos^2 60 + (-6\sqrt{3}) \cos 60 \sin 60 + 7 \sin^2 60 \\ &= 13 \left( \frac{1}{2} \right)^2 – 6\sqrt{3} \left( \frac{1}{2} \right) \left( \frac{\sqrt{3}}{2} \right) + 7 \left( \frac{\sqrt{3}}{2} \right)^2 \\ &= 4, \\ B’ &= 0, \\ C’ &= A \sin^2 \theta – B \sin \theta \cos \theta + C \cos^2 \theta \\ &= 13 \sin^2 60 – (-6\sqrt{3}) \sin 60 \cos 60 + 7 \cos^2 60 \\ &= 13 \left( \frac{\sqrt{3}}{2} \right)^2 + 6\sqrt{3} \left( \frac{\sqrt{3}}{2} \right) \left( \frac{1}{2} \right) + 7 \left( \frac{1}{2} \right)^2 \\ &= 16, \\ D’ &= D \cos \theta + E \sin \theta \\ &= (0) \cos 60 + (0) \sin 60 \\ &= 0, \\ E’ &= -D \sin \theta + E \cos \theta \\ &= -(0) \sin 60 + (0) \cos 60 \\ &= 0, \\ F’ &= F \\ &= -256. \end{aligned} \]La ecuación de la cónica en el sistema de coordenadas rotado se convierte en
\[ 4(x’)^2 + 16(y’)^2 = 256 \] \[ \frac{(x’)^2}{64} + \frac{(y’)^2}{16} = 1. \]Una gráfica de esta sección cónica aparece de la siguiente manera.
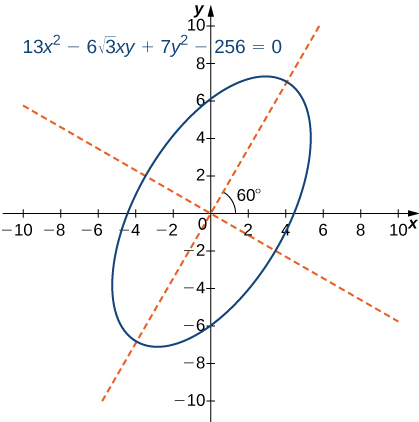
Figura 8.5.14 Gráfica de la elipse descrita por la ecuación 13x² – 6√3 xy + 7y² – 256 = 0.
Los ejes están rotados 60°.
Las líneas rojas discontinuas indican los ejes rotados. ♦
Ejercicio de control 8.5_6
Identifica la cónica y calcula el ángulo de rotación de los ejes para la curva descrita por la ecuación
\[ 3x^2 + 5xy – 2y^2 – 125 = 0. \]♦

Hola, buenos días,
Excelente sus publicaciones, me han servido muchísimo.
Una pregunta donde encuentro mas sobre la hipérbola o sobre el tema “8.5.3 Identificar la ecuación de una hipérbola en forma estándar con focos dados”
Muchas gracias,
Saludos
Hola Felix.
Gracias por el comentario.
Más tarde, luego de publicar un video que estoy realizando, procederé a publicar sobre lo referente al Capítulo 8.5.3 👀
Saludos! 😺
Ya puede ver los apuntes sobre la hipérbola en https://calculo21.com/secciones-conicas/3/ 👀