| 9. Ecuaciones diferenciales | Índice completo del libro de Zill |
1. INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES
-
- 1.1. Definiciones y terminología
- 1.2. Problemas con valores iniciales
- 1.3. Ecuaciones diferenciales como modelos matemáticos
1.1. Definiciones y terminología
En los problemas 1 a 8 establezca el orden de la ecuación diferencial ordinaria dada. Determine si la ecuación es lineal o no lineal, comparando con la ecuación
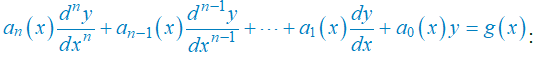
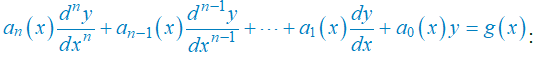
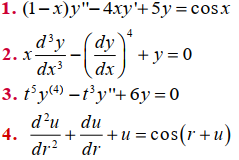
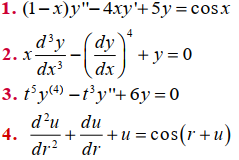


En los problemas 9 y 10 establezca si la ecuación diferencial de primer orden dada es lineal en la variable dependiente comparándola con la ecuación




En los problemas ll a 14, compruebe que la función indicada es una solución de la ecuación diferencial dada. Suponga un intervalo I de definición adecuado para cada solución.


En los problemas 15 a 18 compruebe que la función indicada y = ∅(x) es una solución explícita de la ecuación diferencial de primer orden dada. Proceda como en el ejemplo 2, considerando a ∅ simplemente como una función, dando su dominio. Después considere a ∅ como una solución de la ecuación diferencial, dando al menos un intervalo I de definición.
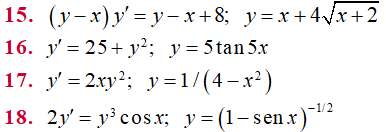
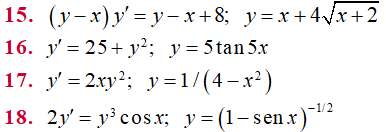
En los problemas 19 y 20 compruebe que la expresión indicada es una solución implícita de la ecuación diferencial dada. Encuentre al menos una solución explícita y = ∅(x) en cada caso. Use alguna aplicación para trazar gráficas para obtener la gráfica de una solución explícita. Dé un intervalo I de definición de cada solución ∅.


En los problemas 21 a 24 compruebe que la familia de funciones indicada es una solución de la ecuación diferencial dada. Suponga un intervalo I de definición adecuado para cada solución.










En los problemas 27 a 30 determine los valores de m tales que la función
y = e ͫ ˣ sea una solución de la ecuación diferencial dada.
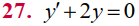
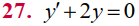






En los problemas 31 y 32 determine los valores de m tales que la función
y = x ͫ sea una solución de la ecuación diferencial dada.




En los problemas 33 a 36 use el concepto de que y = c, −∞ < x < ∞ , es una función constante si y sólo si y′ = 0 para determinar si la ecuación diferencial tiene soluciones constantes.
33. 3xy′ + 5y = 10
34. y′ = y2 + 2y − 3
35. (y − 1)y′ = 1
36. y″ + 4y′ + 6y = 10
En los problemas 37 y 38 compruebe que el par de funciones indicado es una solución del sistema dado de ecuaciones diferenciales en el intervalo (−∞, ∞).





Buenos días, no sabe si existe el solucionario de ecuaciones diferenciales con problemas de valores de la frontera dennis zill 9 edición?
Hola. Las ediciones 9 tiene nueve capítulos, la edición 7 tiene esos mismos capítulos (es idéntico el contenido de estos primeros nueve capítulos) y 6 capítulos adicionales, esto es, tiene 15 capítulos.
Los enlaces para acceder a la solución de los ejercicios que he publicado de estos libros de Zill están en el siguiente pdf. No conozco otro solucionario. https://calculo21.com/ejercicios-resueltos-del-capitulo-9/ 😺👀
Hola! no pude ver la solucion del num. 33 y 35 :/
Hola
Las soluciones de estos ejercicios están en http://bancomate.blogspot.com/search/label/Zill%201.1
En los próximos días voy a reparar los enlaces del PDF 😺👀