| 1. Funciones y sus gráficas | 1.1. Revisión de funciones |

Combinando funciones

Ahora que hemos revisado las características básicas de las funciones, vamos a ver cómo podemos combinar funciones de diferentes maneras, usando operaciones matemáticas básicas para crear nuevas funciones. Por ejemplo, si la función C(x) describe el costo de una empresa para fabricar x artículos y la función R(x) describe los ingresos generados por la venta de esos x artículos, el beneficio obtenido (utilidad) de la fabricación y venta de los x elementos se define como P(x) = R(x) − C(x); esto es, usando la diferencia entre dos funciones, creamos una nueva función.

Alternativamente, podemos crear una nueva función componiendo dos funciones. Por ejemplo, dadas las funciones f (x) = x²  y  g(x) = 3x + 1, la función compuesta f ∘ g se define de manera que

( f ° g) (x) = f (g(x)) = (g(x)) ² = (3x + 1) ².

La función compuesta g ∘ f se define de modo que

( g ∘ f )(x) = g ( f (x)) = 3f (x) + 1 = 3x² + 1.

Tenga en cuenta que estas dos nuevas funciones son diferentes entre sí.

Combinando funciones con operadores aritméticos

Para combinar funciones usando operadores aritméticos, simplemente escribimos las funciones con el operador y simplificamos. Dadas dos funciones f  y  g, podemos definir cuatro nuevas funciones:

( f + g) (x) = f (x) + g (x)                   Suma

( f − g) (x) = f (x) − g (x)                   Diferencia

( f ⋅ g) (x) = f (x) ⋅ g(x)                       Producto

( f / g) (x) = f (x) / g (x),  g (x) ≠ 0         Cociente

EJEMPLO ILUSTRATIVO 1.1_6. Combinando Funciones Usando Operadores Matemáticos

Dadas las funciones f (x) = 2x − 3  y  g(x) = x² − 1, encuentre cada una de las siguientes funciones y establezca su dominio.

a. (f + g) (x)
b. (f − g) (x)
c. (f⋅g) (x)
d. (f /g) (x)

Solución:
a. (f + g) (x) = (2x − 3) + (x² − 1) = x² + 2x − 4. El dominio de esta función es el intervalo (−∞, ∞).
b. (f − g) (x) = (2x − 3) – (x² − 1) = –x² + 2x − 2. El dominio de esta función es el intervalo (−∞, ∞).
c. (f⋅g) (x) = (2x − 3) (x² − 1) = 2x³ − 3x² − 2x + 3. El dominio de esta función es el intervalo (−∞, ∞).
d. (f /g) (x) = (2x − 3)/(x² −1). El dominio de esta función es {x | x ≠ ± 1}.

Ejercicio de control 1.1_4

Para f (x) = x² + 3  y  g(x) = 2x − 5, encuentre (f/g)(x) y establezca su dominio.

Composición  de funciones

Cuando componemos funciones, tomamos una función de una función. Por ejemplo, suponga que la temperatura T en un día dado se describe como una función del tiempo t (medido en horas después de la medianoche) como en la Tabla 1.1. Suponga que el costo C, para calentar o enfriar un edificio durante 1 hora, puede describirse como una función de la temperatura T. Combinando estas dos funciones, podemos describir el costo de calentar o enfriar un edificio como una función del tiempo evaluando C(T(t)). Hemos definido una nueva función, denominada C∘T, que se define de manera tal que (C∘T)(t) = C(T(t)) para todas las t en el dominio de T. Esta nueva función se denomina función compuesta. Notamos que dado que el costo es una función de la temperatura y la temperatura es una función del tiempo, tiene sentido definir esta nueva función (C∘T)(t). No tiene sentido considerar (T∘C)(t), porque la temperatura no es una función del costo.

Definición 1.1_2. Función compuesta

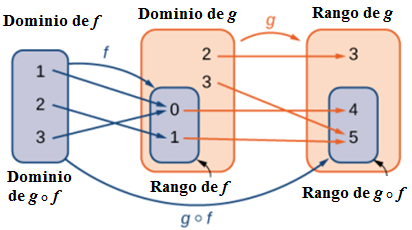
Una función compuesta  se puede ver en dos pasos. Primero, la función  f mapea cada entrada x en el dominio de f a su salida  f (x) en el rango de f. Segundo, ya que el rango de f es un subconjunto del dominio de g, la salida  f(x) es un elemento en el dominio de g, y por lo tanto se asigna a una salida g( f(x) ) en el rango de g. En la siguiente figura 1.8 vemos una ilustración visual de una función compuesta.

EJEMPLO ILUSTRATIVO 1.1_7. Composiciones de funciones definidas por fórmulas

Considere las funciones f (x) = x² + 1 y g(x) = 1 / x.
a. Encuentre (g ∘ f)(x) y establezca su dominio y rango.
b. Evalúe (g ∘ f)(4), (g ∘ f)(-1/2).
c. Encuentre (f ∘ g)(x) y establezca su dominio y rango.
d. Evalúe (f ∘ g)(4), (f ∘ g)(-1/2).

Solución:
a. Podemos encontrar la fórmula para (g ∘ f)(x) de dos maneras diferentes. Podríamos escribir

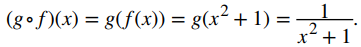
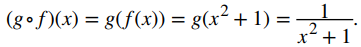
Alternativamente, podríamos escribir

Como x² + 1 ≠ 0 para todos los números reales x, el dominio de (g ∘ f)(x) es el conjunto de todos los números reales. Como 0 < 1 / (x² + 1) ≤ 1, el rango es, como máximo, el intervalo (0, 1]. Para mostrar que el rango es todo este intervalo, dejamos y = 1 / (x² + 1) y resuelva esta ecuación para x para mostrar que para todo y en el intervalo (0, 1], existe un número real x tal que y = 1 / (x² + 1). Al resolver esta ecuación para x, vemos que x² + 1 = 1 / y, lo que implica que

Si y está en el intervalo (0, 1], la expresión debajo del radical no es negativa y, por lo tanto, existe un número real x tal que 1 / (x² + 1) = y. Concluimos que el rango de g ∘ f es el intervalo (0, 1].

c. Podemos encontrar una fórmula para (f ∘ g) (x) de dos maneras. Primero, podemos escribir

Alternativamente, podríamos escribir

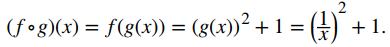
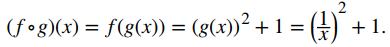
El dominio de f ∘ g es el conjunto de todos los números reales x tal que x ≠ 0. Para encontrar el rango de f, necesitamos encontrar todos los valores de y para los cuales existe un número real x ≠ 0 tal que

Al resolver esta ecuación para x, vemos que necesitamos x para satisfacer

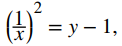
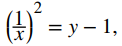
que se simplifica a

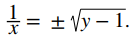
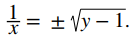
Finalmente obtenemos

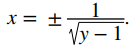
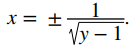
Como 1 / √(y − 1) es un número real si y solo si y > 1, el rango de f es el conjunto {y | y > 1}.

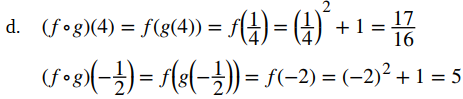
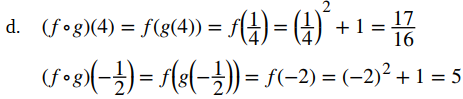
Ejercicio de control 1.1_5

Sea f (x) = 2 − 5x  y  g(x) = √x. Encuentra (f∘g)(x).

En el ejemplo anterior, podemos ver que (f ∘ g) (x) ≠ (g ∘ f) (x). Esto nos dice, en términos generales, que el orden en que componemos las funciones es importante.

EJEMPLO ILUSTRATIVO 1.1_8. Composición de funciones definidas por tablas

Considere las funciones f  y  g descritas en la Tabla 1.1_4 y la Tabla 1.1_5.

a. Evalúe (g ∘ f)(3), (g ∘ f)(0).
b. Indique el dominio y el rango de (g ∘ f)(x).
c. Evalúe (f ∘ f)(3), (f ∘ f)(1).
d. Indique el dominio y el rango de (f ∘ f)(x).

Solución:

b. El dominio de g ∘ f es el conjunto {−3, −2, −1, 0, 1, 2, 3, 4}. Como el rango de f es el conjunto {−2, 0, 2, 4}, el rango de g ∘ f es el conjunto {0, 3, 5}.

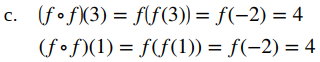
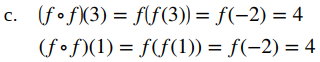
d. El dominio de f ∘ f es el conjunto {−3, −2, −1, 0, 1, 2, 3, 4}. Como el rango de f es el conjunto {−2, 0, 2, 4}, el rango de f ∘ f  es el conjunto {0, 4}.

EJEMPLO ILUSTRATIVO 1.1_9. Aplicación que implica una función compuesta

Una tienda anuncia una venta del 20% de descuento en toda la mercancía. Carolina tiene un cupón que le da derecho a un 15% de descuento adicional en cualquier artículo, incluida la mercancía en oferta. Si Carolina decide comprar un artículo con un precio original de x dólares, ¿cuánto terminará pagando si aplica su cupón al precio de venta? Resuelva este problema utilizando una función compuesta.

Solución:
Dado que el precio de venta es 20% de descuento sobre el precio original, si un artículo tiene un precio original de x dólares, su precio de venta viene dado por f (x) = 0.80x. Dado que el cupón da derecho a un 15% de descuento en el precio de cualquier artículo, si un artículo tiene un precio de y dólares, el precio, después de aplicar el cupón, viene dado por g(y) = 0.85y. Por lo tanto, si el precio es originalmente de x dólares, su precio de venta será f (x) = 0.80x y luego su precio final después del cupón será g(f (x)) = 0.85 (0.80x) = 0.68x.

Ejercicio de control 1.1_6

Si los artículos están a la venta con un 10% de descuento sobre su precio original, y un cliente tiene un cupón para un descuento adicional del 30%, ¿cuál será el precio final para un artículo que originalmente es x dólares, después de aplicar el cupón al precio de venta?

Simetría de funciones

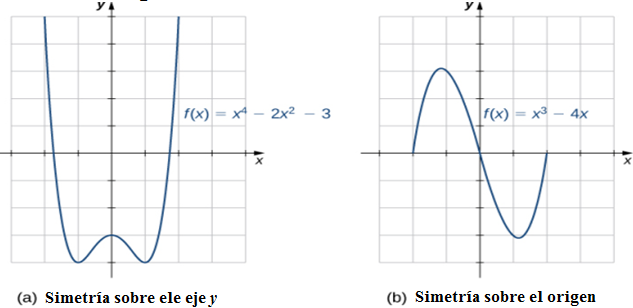
Las gráficas de ciertas funciones tienen propiedades de simetría que nos ayudan a comprender la función y la forma de su gráfica. Por ejemplo, considere la función f(x) = x⁴ − 2x² − 3 que se muestra en la figura 1.1_12 (a). Si tomamos la parte de la curva que se encuentra a la derecha del eje y y la giramos sobre este eje, queda exactamente igual a la curva trazada a la izquierda del eje y En este caso, decimos que la función tiene simetría sobre el eje y. Por otro lado, considere la función f (x) = x³ − 4x que se muestra en la Figura 1.1_12 (b). Si tomamos la gráfica y la giramos 180 ° alrededor del origen, la nueva gráfica se verá exactamente igual. En este caso, decimos que la función tiene simetría sobre el origen.

Función par y función impar

Si se nos da la gráfica de una función, es fácil ver si la gráfica tiene una de estas propiedades de simetría. Pero sin una gráfica, ¿cómo podemos determinar algebraicamente si una función f  tiene simetría? Mirando nuevamente la Figura 1.9, vemos que dado que f es simétrica respecto al eje y, si el punto (x, y) está en la gráfica, el punto (− x, y) también está en la gráfica. En otras palabras, f (− x) = f (x). Si una función f tiene esta propiedad, decimos que f , que tiene simetría sobre el eje y es una función par. Por ejemplo, f (x) = x² es una función par porque

f (− x) = (− x )² = x² = f (x).

Por el contrario, mirando de nuevo la figura 1.9, si una función f es simétrica respecto del origen, cuando el punto (x, y) está en la gráfica, el punto (− x, − y) también está en la gráfica. En otras palabras, f (− x) = − f (x). Si f tiene esta propiedad, decimos que f, que tiene simetría sobre el origen, es una función impar. Por ejemplo, f (x) = x³ es impar porque

f (− x) = (− x)³ = − x³ = − f (x).

Definición 1.1_3. Función par y función impar

Si  f (x) = f (− x) para todas las x en el dominio de f, entonces f es una función par. Una función par es simétrica con respecto al eje y.

Si f (− x) = – f (x) para todas las x en el dominio de f, entonces f es una función impar. Una función impar es simétrica sobre el origen.

EJEMPLO ILUSTRATIVO 1.1_10. Funciones pares e impares

Determine si cada una de las siguientes funciones es par, impar o ninguna.

Solución:
Para determinar si una función es par o impar, evaluamos f (−x) y la comparamos con f (x) y −f (x).

Por lo tanto, f es par.

Ahora, f (−x) ≠ f (x). Además, observando que

vemos que f (−x) ≠ −f (x). Por lo tanto, f no es par ni impar.

Por lo tanto, f es impar.

Ejercicio de control 1.1_7

Determine si f (x) = 4x³ − 5x es par, impar o ninguno.

Función valor absoluto

Una función simétrica que surge con frecuencia es la función de valor absoluto, escrita como |x|. La función de valor absoluto se define como

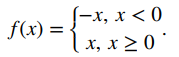
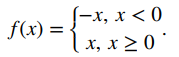
Algunos estudiantes describen esta función al afirmar que “hace que todo sea positivo”. Por la definición de la función de valor absoluto, vemos que si x < 0, entonces | x | = −x > 0, y si  x > 0, entonces | x | = x > 0. Sin embargo, para x = 0, | x | = 0. Por lo tanto, es más exacto decir que para todas las entradas distintas de cero, la salida es positiva, pero si x = 0, la salida | x | = 0. Concluimos que el rango de la función de valor absoluto es {y | y ≥ 0}. En la figura 1.1._13, vemos que la función de valor absoluto es simétrica con respecto al eje y y, por lo tanto, es una función par.

EJEMPLO ILUSTRATIVO 1.1_11. Trabajando con la función de valor absoluto

Encuentre el dominio y el rango de la función f (x) = 2 | x − 3 | + 4.

Solución:
Dado que la función de valor absoluto se define para todos los números reales, el dominio de esta función es (−∞, ∞). Dado que | x − 3 | ≥0  para todo x, la función f (x) = 2 | x − 3 | + 4 ≥ 4. Por lo tanto, el rango es, como máximo, el conjunto {y | y ≥ 4}. Para ver que el rango es, de hecho, todo este conjunto, necesitamos mostrar que para y ≥ 4 existe un número real x tal que

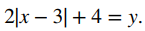
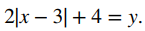
Un número real x satisface esta ecuación siempre que

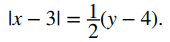
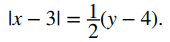
Como y ≥ 4, sabemos que y − 4 ≥ 0 y, por lo tanto, el lado derecho de la ecuación no es negativo, por lo que es posible que haya una solución. Además,

Por lo tanto, vemos que hay dos soluciones:

El rango de esta función es el conjunto {y | y ≥ 4}.

Ejercicio de control 1.1_8

Para la función f (x) = |x + 2| − 4, encuentre el dominio y el rango.