| 1. Funciones y sus gráficas | 1.1. Revisión de funciones |
Representando funciones
Típicamente, una función se representa usando una o más de las siguientes herramientas:
- Una tabla
- Una gráfica
- Una fórmula
Podemos identificar una función en cada forma, pero también podemos usarlas juntas. Por ejemplo, podemos trazar en una gráfica los valores de una tabla o crear una tabla de valores a partir de una fórmula.
Tablas
Las funciones descritas utilizando una tabla de valores surgen con frecuencia en aplicaciones del mundo real. Considere el siguiente ejemplo sencillo. Podemos describir la temperatura en un día determinado en función de la hora del día. Supongamos que registramos la temperatura cada hora durante un período de 24 horas a partir de la medianoche. Dejamos que nuestra variable de entrada x sea el tiempo después de la medianoche, medido en horas, y la variable de salida y sea la temperatura x horas después de la medianoche, medida en grados Fahrenheit. Registramos nuestros datos en la Tabla 1.1_1.
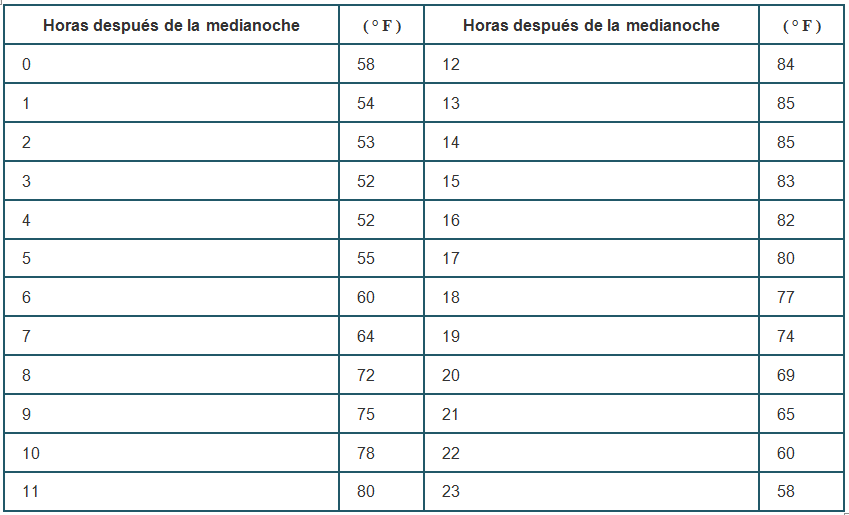
Podemos ver en la tabla que la temperatura es una función del tiempo, y que la temperatura disminuye, luego aumenta y luego disminuye nuevamente. Sin embargo, no podemos obtener una imagen clara del comportamiento de la función sin representarla gráficamente.
Gráficas de funciones
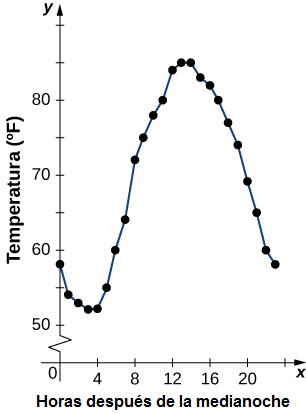
Dada una función f descrita por una tabla, podemos proporcionar una imagen visual de la función en forma de gráfico. Graficar las temperaturas enumeradas en la Tabla 1.1_1 puede darnos una mejor idea de su fluctuación a lo largo del día. La figura 1.1_4 muestra la gráfica de la función de temperatura.
Tengamos presente que podemos visualizar una función trazando puntos (x, y) en el plano de coordenadas donde y = f (x). La gráfica de una función es el conjunto de todos estos puntos. En nuestro ejemplo, se marcan en el plano cartesiano los puntos que representan los datos de la tabla. En el eje horizontal se señalan las horas del día (abscisa del punto: primer elemento del par ordenado). En el eje vertical se señalan las temperaturas (ordenada del punto: segundo elemento del par ordenado).


A partir de los puntos trazados en el gráfico de la Figura 1.1_4, podemos visualizar la forma general de la gráfica de la función. A menudo es útil conectar los puntos en la gráfica, que representan los datos de la tabla. En este ejemplo, aunque no podemos llegar a una conclusión definitiva con respecto a la temperatura en ningún momento para el que no se registró la temperatura, dada la cantidad de puntos de datos recopilados y el patrón en estos puntos, es razonable sospechar que las temperaturas en otros momentos siguieron un patrón similar, como podemos ver en la Figura 1.1_5.

Fórmulas Algebraicas
A veces no se nos dan los valores de una función en forma de tabla, sino que se nos dan los valores en una fórmula explícita. Las fórmulas surgen en muchas aplicaciones. Por ejemplo, el área de un círculo de radio r viene dada por la fórmula A(r) = πr². Cuando un objeto se lanza hacia arriba desde el suelo con una velocidad inicial v0 pies/s, su altura sobre el suelo desde el momento en que se arroja hasta que vuelve a tocar el suelo viene dada por la fórmula s(t) = – 16t² + v0t. Cuando se invierten P dólares en una cuenta a una tasa de interés anual r compuesta continuamente, la cantidad de dinero después de t años viene dada por la fórmula A(t) = Pe^(rt). Las fórmulas algebraicas son herramientas importantes para calcular valores de funciones. A menudo también representamos estas funciones dadas por una fórmula visualmente en forma de una gráfica.
Dada una fórmula algebraica para una función f, la gráfica de f es el conjunto de puntos (x, f (x)), donde x está en el dominio de f y f (x) está en el rango. Para graficar una función dada por una fórmula, es útil comenzar usando la fórmula para crear una tabla de entradas y salidas. Si el dominio de f consiste en un número infinito de valores, no podemos enumerarlos todos, pero dado que enumerar algunas de las entradas y salidas puede ser muy útil, a menudo es una buena manera de comenzar.
Ceros de una función
Al crear una tabla de entradas y salidas, generalmente verificamos si el cero es una salida. Los valores de x donde f (x) = 0 se llaman ceros de una función. Por ejemplo, los ceros de f (x) = x² − 4 son x = ± 2. Los ceros determinan dónde la gráfica de f se cruza con el eje x, lo que nos da más información sobre la forma de la gráfica de la función. La gráfica de una función puede nunca cruzarse con el eje x, o puede cruzarse múltiples (o incluso infinitamente) veces.
Otro punto de interés es la intersección con el eje y, si existe. La intersección en y está dada por (0, f (0)).
Prueba de la recta vertical
Como una función tiene exactamente una salida para cada entrada, el gráfico de una función puede tener, como máximo, una intersección en y. Si x = 0 está en el dominio de una función f, entonces f tiene exactamente una intersección en y. Si x = 0 no está en el dominio de f, entonces f no tiene intercepción y. De manera similar, para cualquier número real c, si c está en el dominio de f, hay exactamente una salida f (c), y la recta x = c intersecta la gráfica de f exactamente una vez. Por otro lado, si c no está en el dominio de f, f (c) no está definida y la recta x = c no intersecta la gráfica de f. Esta propiedad se resume en la prueba de la recta vertical.
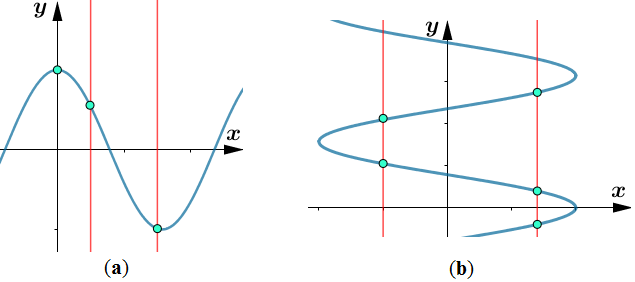
Dada una función f, cada recta vertical que se puede dibujar intersecta la gráfica de f no más de una vez. Si alguna recta vertical intersecta un conjunto de puntos más de una vez, el conjunto de puntos no representa una función.
Podemos usar esta prueba para determinar si un conjunto de puntos dados en el plano representa la gráfica de una función (Figura 1.1_6).

EJEMPLO ILUSTRATIVO 1.1_3. Encontrar ceros e intersecciones de una función
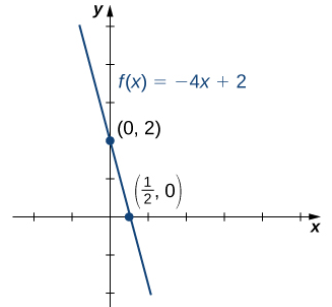
Considere la función f (x) = – 4x + 2.
a. Encuentra todos los ceros de f.
b. Encuentre la intersección con el eje y (si la hay).
c. Dibuja una gráfica de f.
Solución:
a. Para encontrar los ceros, resuelve f (x) = – 4x + 2 = 0. Descubrimos que f tiene un cero en x = 1/2.
b. La intersección en y está dada por (0, f (0)) = (0, 2).
c. Dado que f es una función lineal de la forma f (x) = mx + b que pasa por los puntos (1/2, 0) y (0, 2), podemos dibujar fácilmente la gráfica de f :

EJEMPLO ILUSTRATIVO 1.1_4. Uso de ceros e -Interceptos para dibujar la gráfica de una función
Considere la función f (x) = √(x + 3) + 1.
a. Encuentra todos los ceros de f.
b. Encuentre la intersección con el eje y (si la hay).
c. Dibuja una gráfica de f.
Solución:
a. Para encontrar los ceros, resuelve √(x + 3) + 1 = 0. Esta ecuación implica √(x + 3) = −1. Como √(x + 3) ≥ 0 para todas las x, esta ecuación no tiene soluciones y, por lo tanto, f no tiene ceros.
b. La intersección en y está dada por (0, f (0)) = (0, √3 + 1).
c. Para graficar esta función, hacemos una tabla de valores. Como necesitamos que x + 3 ≥ 0, debemos elegir valores de x ≥ − 3. Elegimos valores que hacen que la función de raíz cuadrada sea fácil de evaluar.
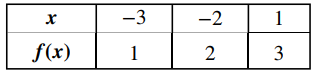

Haciendo uso de la tabla y sabiendo que, dado que la función es una raíz cuadrada, la gráfica de f debería ser similar a la gráfica de y = √x, dibujamos la gráfica:

Ejercicio de control 1.1_3
Encuentre los ceros de la función f (x) = x³ − 5x² + 6x.
EJEMPLO ILUSTRATIVO 1.1_5. Encontrar la altura de un objeto en caída libre
Si una pelota cae desde una altura de 100 pies, su altura s en el tiempo t viene dada por la función s(t) = – 16t² + 100, donde s se mide en pies y t se mide en segundos. El dominio está restringido al intervalo [0, c], donde t = 0 es el momento en que se suelta la pelota y t = c es el momento en que la pelota toca el suelo.
a. Cree una tabla de valores que muestre la altura s(t) cuando t = 0, 0.5, 1, 1.5, 2 y 2.5. Usando los datos de la tabla, determine el dominio para esta función. Es decir, encuentre el tiempo c cuando la pelota toca el suelo.
b. Dibuja una gráfica de s.
Solución:


Como la pelota toca el suelo cuando t = 2.5, el dominio de esta función es el intervalo [0, 2.5].
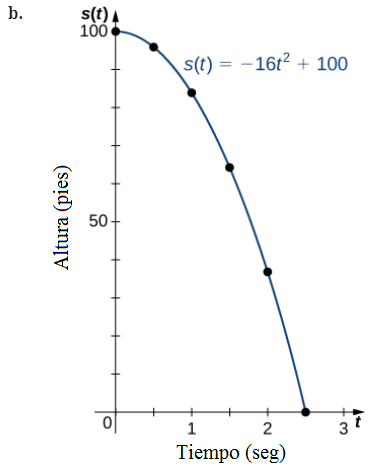

Tenga en cuenta que para esta función y la función f (x) = – 4x + 2 graficada en la Figura 1.1_7, los valores de f (x) se hacen más pequeños a medida que x se hace más grande. Se dice que una función con esta propiedad está decreciendo. Por otro lado, para la función f (x) = √(x + 3) + 1 graficada en la Figura 1.1_8, los valores de f (x) se hacen más grandes a medida que los valores de x se hacen más grandes. Se dice que una función con esta propiedad está creciendo. Sin embargo, es importante tener en cuenta que una función puede aumentar en algún intervalo o intervalos y disminuir en un intervalo o intervalos diferentes. Por ejemplo, usando nuestra función de temperatura en la Figura 1.1_5, podemos ver que la función está decreciendo en el intervalo (0, 4), creciendo en el intervalo (4, 14) y luego decreciendo en el intervalo (14, 23). Hacemos que la idea de una función que aumente o disminuya en un intervalo particular sea más precisa en la siguiente definición.
Funciones crecientes y decrecientes
Decimos que una función f está creciendo en un intervalo I si para todo x1, x2∈I,
f (x1) ≤ f (x2) cuando x1 < x2.
Decimos que f crece estrictamente en el intervalo I si para todo x1, x2∈I,
f (x1) < f (x2) cuando x1 < x2.
Decimos que una función f está decreciendo en el intervalo I si para todos x1, x2∈I,
f (x1) ≥ f (x2) cuando x1 < x2.
Decimos que una función f está decreciendo estrictamente en el intervalo I si para todos x1, x2∈I
f (x1) > f (x2) cuando x1 < x2.
Por ejemplo, la función f (x) = 3x aumenta en el intervalo (−∞, ∞) porque 3x1 < 3x2 siempre que x1 < x2. Por otro lado, la función f (x) = − x3 está disminuyendo en el intervalo (−∞, ∞) porque f (x1) > f (x2) siempre que x1 > x2 (Figura 1.7)
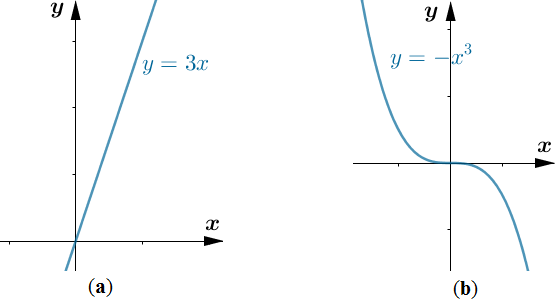
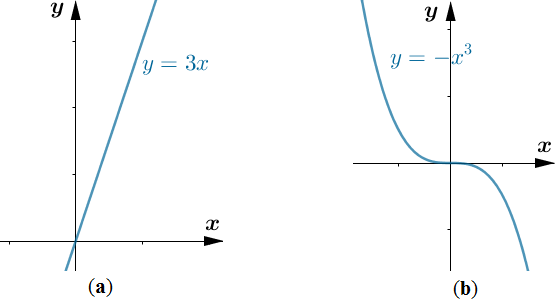

Muy práctica toda la información de ésta página, recomendable para repaso de cálculo…
Bienvenido!