| Álgebra lineal con aplicaciones | 2. Álgebra de matrices |

2.4 Matrices Inversas

       Tres operaciones básicas sobre matrices, suma, multiplicación y resta, son análogos para matrices que las mismas operaciones para números escalares. En esta sección presentamos el análogo para matrices de la división numérica.

Para comenzar, considere cómo se resuelve una ecuación numérica ax = b cuando a y b son números conocidos. Si a = 0, no hay solución (a menos que b = 0). Pero si a ≠ 0, podemos multiplicar ambos lados por el inverso a⁻¹ = 1/a para obtener la solución x = a⁻¹b. Por supuesto, multiplicar por a⁻¹ es solo dividir por a, y la propiedad de a⁻¹ que hace que esto funcione es que a⁻¹a = 1. Además, vimos en la Sección 2.2 que el papel que juega 1 en la aritmética se juega en álgebra matricial por la matriz de identidad I. Esto sugiere la siguiente definición.

Definición 2.4.1 Matrices Inversas

Si A es una matriz cuadrada, una matriz B se llama inversa de A si y sólo si

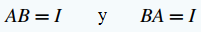
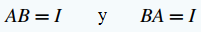
Una matriz A que tiene una inversa se llama matriz invertible. ♦

Nota: Solo las matrices cuadradas tienen inversas. Aunque es plausible que las matrices no cuadradas A y B puedan existir de manera tal que AB = I_m y BA = I_n, donde A es una matriz de tamaño m×n y B una de n×m, afirmamos que esto fuerza a que n = m. De hecho, si m < n existe una columna x distinta de cero tal que Ax = 0 (según el Teorema 1.3.1), entonces x = I_nx = (BA)x = B(Ax) = B(0) = 0, una contradicción. Por lo tanto, m ≥ n. Del mismo modo, la condición AB = I_m implica que n ≥ m. Por lo tanto, m = n, entonces A es una matriz cuadrada.

Ejemplo ilustrativo 2.4_1

Muestre que

es una inversa de 

Solución:

Calcule AB y BA,

Por lo tanto, AB = I = BA, entonces B es de hecho una inversa de A. ♦

Ejemplo ilustrativo 2.4_2

Demuestre que la matriz no tiene inversa.

Solución:

Si es una matriz arbitraria de tamaño 2×2, de tal modo que

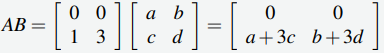
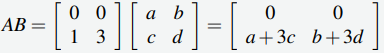
entonces AB tiene una fila de ceros. Por lo tanto, AB no puede ser igual a I para cualquier B. ♦

      El argumento del ejemplo 2.4.2 muestra que ninguna matriz cero tiene inversa. Pero el ejemplo 2.4.2 también muestra que, a diferencia de la aritmética, es posible que una matriz distinta de cero no tenga inversa. Sin embargo, si una matriz tiene una inversa, solo tiene una.

Teorema 2.4.1

Si B y C son ambas inversas de A, entonces B = C. ♦

Prueba. Como B y C son ambas inversas de A, tenemos CA = I = AB. Por eso

B = IB = (CA)B = C(AB) = CI = C  ♦

      Si A es una matriz invertible, la inversa (única) de A se denota A⁻¹. Por lo tanto, A⁻¹ (cuando existe) es una matriz cuadrada del mismo tamaño que A con la propiedad de que

AA⁻¹ = I  y  A⁻¹A = I

Estas ecuaciones caracterizan A⁻¹ en el siguiente sentido:

Criterio Inverso: Si de alguna manera se puede encontrar una matriz B tal que AB = I  y  BA = I, entonces A es invertible y B es la inversa de A; en símbolos, B = A⁻¹.

Esta es una forma de verificar que existe la inversa de una matriz. El Ejemplo 2.4.3 y el Ejemplo 2.4.4 ofrecen ilustraciones.

Ejemplo ilustrativo 2.4_3

Sea, demostrar que A³ = I y así encontrar A⁻¹

Solución:

Se tiene que y además 

Por lo tanto, A³ = I, como se afirma. Esto se puede escribir como A²A = I = AA², por lo que se tiene que A² es el inverso de A. Es decir, ♦

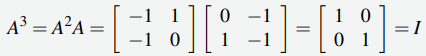
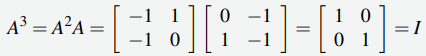
      El siguiente ejemplo presenta una fórmula útil para hallar la inversa de una matriz de 2 × 2 cuando existe. Para decirlo, definimos el determinante det A y el adjunto adj A de la matriz A de la siguiente manera:

  y 

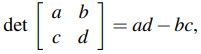
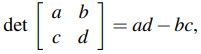
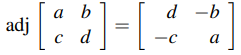
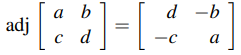
Ejemplo ilustrativo 2.4_4

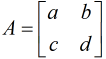
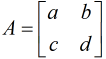
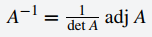
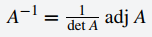
Sea , demostrar que A tiene inversa si y solo si det A ≠ 0, y en este caso

Solución:

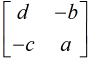
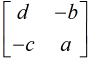
Por conveniencia, escriba e = det A = ad − bc   y   B = adj A = . Entonces AB = eI = BA como el lector puede verificar. Entonces si e ≠ 0, la multiplicación escalar por 1/e da

De donde, A es invertible y A⁻¹ = (1/e)B. Por lo tanto, solo queda demostrar que si A⁻¹ existe, entonces e ≠ 0. Probamos esto mostrando que asumir e = 0 conduce a una contradicción. De hecho, si e = 0, entonces AB = eI = 0, entonces la multiplicación a la izquierda por A⁻¹ da A⁻¹AB = A⁻¹0; es decir, IB = 0, por lo que B = 0. Pero esto implica que a, b, c y d son todos cero, por lo que A = 0, contrariamente a la suposición de que existe A⁻¹. ♦

 A modo de ilustración, si entonces det A = 2 · 8 − 4 ·(−3) = 28 6 = 0. Por tanto, A es invertible y

Como se invita al lector a verificar.

      El determinante y el conjugado se definirán en el Capítulo 3 para cualquier matriz cuadrada, y las conclusiones del Ejemplo 2.4.4 se demostrarán con toda su generalidad.

Matrices inversas y sistemas lineales

Las matrices inversas se pueden utilizar para resolver ciertos sistemas de ecuaciones lineales. Recuerde que un sistema de ecuaciones lineales se puede escribir como una sola ecuación matricial

Ax = b

donde A y b son conocidos y x debe determinarse. Si A es invertible, multiplicamos cada lado de la ecuación de la izquierda por A⁻¹ para obtener

Esto da la solución al sistema de ecuaciones (el lector debe verificar que x = A⁻¹b realmente satisface Ax = b). Además, el argumento muestra que si x es cualquier solución, entonces necesariamente x = A⁻¹b, por lo que la solución es única. Por supuesto, la técnica funciona solo cuando la matriz de coeficientes A tiene una inversa. Esto prueba el Teorema 2.4.2.

Teorema 2.4.2

Suponga que un sistema de n ecuaciones en n variables se escribe en forma matricial como

Ax = b

Si la matriz A de coeficientes n×n es invertible, el sistema tiene la solución única

♦