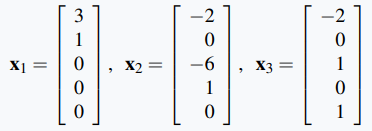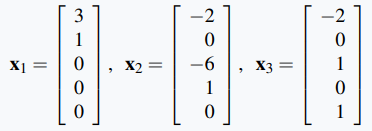Álgebra lineal con aplicaciones 

| 1. Sistema de ecuaciones lineales | Ejercicios propuestos del Capítulo 1.3 |

  1.3   Ecuaciones homogéneas  

       Un sistema de ecuaciones en las variables

se llama homogéneo si todos los términos constantes son cero, es decir, si cada ecuación del sistema tiene la forma

Claramente

es una solución para tal sistema; se llama la solución trivial. Cualquier solución en la que al menos una variable tenga un valor distinto de cero se llama solución no trivial. Nuestro objetivo principal en esta sección es proporcionar una condición útil para que un sistema homogéneo tenga soluciones no triviales. El siguiente ejemplo es instructivo.

Ejemplo ilustrativo 1.3_1

Muestre que el siguiente sistema homogéneo tiene soluciones no triviales.

Solución:

La reducción de la matriz aumentada a la forma escalonada reducida por renglón se describe a continuación.

Las variables principales son x₁, x₂ y x₄, por lo que x₃ se asigna como parámetro; por ejemplo, x₃ = t. Entonces la solución general es x₁ = −t, x₂ = t, x₃ = t, x₄ = 0. Por lo tanto, tomando t = 1 (por ejemplo), obtenemos una solución no trivial: x₁ = −1, x₂ = 1, x₃ = 1 , x₄ = 0. ◊

La existencia de una solución no trivial en el Ejemplo 1.3_1 está asegurada por la presencia de un parámetro en la solución. Esto se debe al hecho de que hay una variable no principal (x₃ en este caso). Pero debe haber una variable no principal aquí porque hay cuatro variables y solo tres ecuaciones (y, por lo tanto, como máximo tres variables principales). Esta discusión se generaliza en el siguiente teorema fundamental.

Teorema 1.3.1

Si un sistema homogéneo de ecuaciones lineales tiene más variables que ecuaciones, entonces tiene una solución no trivial (de hecho, infinitas soluciones).

Prueba. Suponga que hay m ecuaciones en n variables donde n  > m, y deje que R denote la forma escalonada reducida por renglones de la matriz aumentada. Si hay r variables principales, hay n − r variables no principales y, por lo tanto, n − r parámetros. Por lo tanto, es suficiente mostrar que r < n. Pero r ≤ m porque R tiene r 1s principales y m filas, y m < n por hipótesis. Entonces r ≤ m < n, que da r < n. ◊

Tenga en cuenta que lo contrario del Teorema 1.3.1 no es cierto: si un sistema homogéneo tiene soluciones no triviales, no necesita tener más variables que ecuaciones (el sistema x₁ + x₂ = 0, 2x₁ + 2x₂ = 0 tiene soluciones no triviales pero m = 2 = n.)
El Teorema 1.3.1 es muy útil en aplicaciones. El siguiente ejemplo proporciona una ilustración de la geometría.

Ejemplo ilustrativo 1.3_2

Llamamos a la gráfica de una ecuación ax² + bxy + cy² + dx + ey + f = 0 una cónica si los números a, b y c no son todos cero. Demuestre que hay al menos una cónica a través de cinco puntos en el plano que no están todos en una misma recta.

Solución:

Deje que las coordenadas de los cinco puntos sean (p₁, q₁), (p₂, q₂), (p₃, q₃), (p₄, q₄) y (p₅, q₅). La gráfica de ax² + bxy + cy² + dx + ey + f = 0 pasa a través de (pᵢ, qᵢ) si

Esto da cinco ecuaciones lineales, una para cada i, en las seis variables a, b, c, d, e y f. Por lo tanto, existe una solución no trivial de acuerdo con el Teorema 1.3.1. Ahora, si a = b = c = 0, los cinco puntos se encuentran en la recta cuya ecuación es dx + ey + f = 0, al contrario de lo que se supone. Por lo tanto, uno de lo valores a, b, c es distinto de cero; por lo que, de acuerdo con la definición de cónica, hay al menos una cónica que pasa por estos cinco puntos. ◊

Combinaciones lineales y soluciones básicas

Como con las filas, dos columnas se consideran iguales si tienen el mismo número de entradas y las entradas correspondientes son las mismas. Sean x e y dos columnas con el mismo número de entradas. Como con las operaciones elementales de fila, su suma x + y se obtiene sumando las entradas correspondientes y, si k es un número, el producto escalar k x se define multiplicando cada entrada de x por k. Más precisamente:

Una suma de múltiplos escalares de varias columnas se denomina combinación lineal de estas columnas. Por ejemplo, s x + t y es una combinación lineal de x e y para cualquier elección de números s y t.

Ejemplo ilustrativo 1.3_3

Ejemplo ilustrativo 1.3_4

Sea

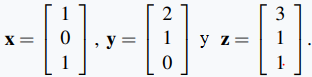
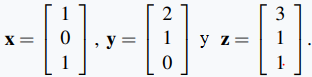
Si

determinar si v y w son combinaciones lineales de x, y y z.

Solución:
Para v, debemos determinar si los números r, s y t existen de modo que v = r x + s y + t z, es decir, si

La ecuación de las entradas correspondientes proporciona un sistema de ecuaciones lineales r + 2s + 3t = 0, s + t = −1, y r + t = 2 para r, s y t. Por eliminación gaussiana, la solución es r = 2 − k, s = −1 − k, y t = k donde k es un parámetro. Tomando k = 0, vemos que v = 2x − y es una combinación lineal de x, y y z. Volviendo a w, buscamos nuevamente r, s, y t de modo que w = r x + s y + t z; es decir,

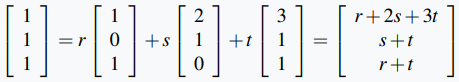
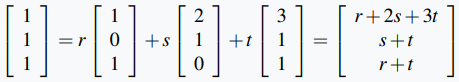
que conducen a las ecuaciones r + 2s + 3t = 1, s + t = 1 y r + t = 1 para los números reales r, s y t. Pero esta vez no hay una solución (que el lector puede verificarlo), por lo que w no es una combinación lineal de x, y y z. ◊

       Nuestro interés en las combinaciones lineales proviene del hecho de que proporcionan una de las mejores formas de describir la solución general de un sistema homogéneo de ecuaciones lineales. Al resolver tal sistema con n variables x₁, x₂, …, x_n, escriba las variables como una matriz columna:

La solución trivial se denota

Como ilustración, la solución general en el Ejemplo 1.3.1 es x₁ = −t, x₂ = t, x₃ = t, y x₄ = 0, donde t es un parámetro, y ahora lo expresamos diciendo que la solución general es

Donde t es arbitrario.

Ahora dejemos que x e y sean dos soluciones para un sistema homogéneo con n variables. Entonces, cualquier combinación lineal s x + t y de estas soluciones resulta ser nuevamente una solución para el sistema. Más generalmente:

Supongamos que una ecuación típica en el sistema es

y además supongamos que

son soluciones. Entonces

Por lo tanto

también es una solución porque

Un argumento similar muestra que esto también es cierto para combinaciones lineales de más de dos soluciones.

Lo notable es que cada solución a un sistema homogéneo es una combinación lineal de ciertas soluciones particulares y, de hecho, estas soluciones se calculan fácilmente utilizando el algoritmo gaussiano. Aquí hay un ejemplo.

Ejemplo ilustrativo 1.3_5

Resolver el siguiente sistema homogéneo con matriz de coeficientes

Solución:
La reducción de la matriz aumentada a la forma escalonada reducida es

entonces las soluciones son x₁ = 2s + (1/5)t, x₂ = s, x₃ = (3/5)t y x₄ = t por eliminación gaussiana. Por lo tanto, podemos escribir la solución general x en forma de matriz

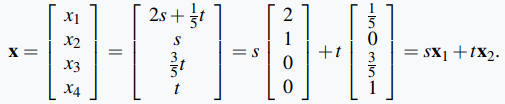
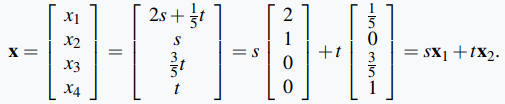
Aquí

son soluciones particulares determinadas por el algoritmo gaussiano. ◊

Las soluciones x₁ y x₂ en el ejemplo anterior se definen de la siguiente manera:

Definición 1.3.1 Soluciones básicas

El algoritmo gaussiano produce sistemáticamente soluciones a cualquier sistema lineal homogéneo, llamadas soluciones básicas, una para cada parámetro.

Además, el algoritmo gaussiano proporciona una forma rutinaria de expresar cada solución como una combinación lineal de soluciones básicas como en el Ejemplo 1.3.5, donde la solución general x se convierte en

Por lo tanto, al introducir un nuevo parámetro r = t/5, podemos multiplicar la solución básica original x₂ por 5 y eliminar así las fracciones. Por esta razón se tiene la siguiente:

Convención: Cualquier múltiplo escalar distinto de cero de una solución básica se seguirá llamando solución básica.

       Del mismo modo, el algoritmo gaussiano produce soluciones básicas para cada sistema homogéneo, una para cada parámetro (no hay soluciones básicas si el sistema solo tiene la solución trivial). Además, cada solución es dada por el algoritmo como una combinación lineal de estas soluciones básicas (como en el Ejemplo 1.3_5).
Si la matriz A tiene rango r, el Teorema 1.2.2 muestra que hay exactamente n − r parámetros y, por lo tanto, n − r soluciones básicas. Esto demuestra el siguiente teorema:

Teorema 1.3.2

Sea A una matriz de tamaño m × n y de rango r, y considere el sistema homogéneo en n variables con A como matriz de coeficientes. Entonces: 1. El sistema tiene exactamente n − r soluciones básicas, una para cada parámetro. 2. Cada solución es una combinación lineal de estas soluciones básicas.

Ejemplo ilustrativo 1.3_6

Encuentre soluciones básicas del sistema homogéneo con matriz de coeficientes A, y exprese cada solución como una combinación lineal de las soluciones básicas, donde

Solución:
La reducción de la matriz aumentada a la forma escalonada reducida por filas es

entonces la solución general es x₁ = 3r −2s − 2t, x₂ = r, x₃ = −6s + t, x₄ = s y x₅ = t donde r, s y t son parámetros. En forma matricial esto queda

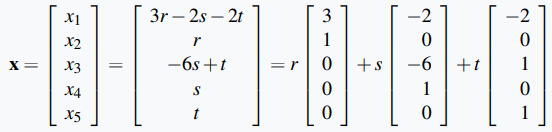
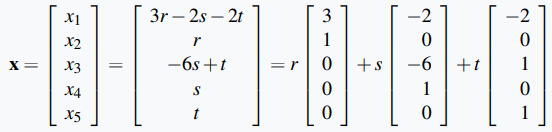
Por lo tanto, las soluciones básicas son