La regla de L’Hôpital

Otras formas indeterminadas

La regla de L’Hôpital es muy útil para evaluar los límites que involucran las formas indeterminadas 0/0 y ∞ / ∞. Sin embargo, también podemos usar la regla de L’Hôpital para ayudar a evaluar los límites que involucran otras formas indeterminadas que surgen al evaluar los límites.

Las expresiones 0⋅∞, ∞ − ∞, 1^∞, ∞⁰ y 0⁰ se consideran formas indeterminadas. Estas expresiones no son números reales. Más bien, representan formas que surgen cuando se intenta evaluar ciertos límites. A continuación veremos por qué son formas indeterminadas y luego mostramos cómo usar la regla de L’Hôpital en estos casos. La idea clave es que debemos reescribir las formas indeterminadas de tal manera que lleguemos a la forma indeterminada 0/0 o ∞ / ∞.

Forma indeterminada de tipo 0⋅∞

Supongamos que queremos evaluar lim _{x → a} (f (x) ⋅ g (x)), donde f (x) → 0 y g (x) → ∞ (o −∞) cuando x → a. Dado que un término en el producto se acerca a cero pero el otro término se está volviendo arbitrariamente grande (en magnitud), cualquier cosa puede pasarle al producto. Usamos la notación 0⋅∞ para denotar la forma que surge en esta situación. La expresión 0⋅∞ se considera indeterminada porque no podemos determinar sin un análisis más detallado el comportamiento exacto del producto f (x) ⋅ g (x) cuando x → a.

Por ejemplo, sea n un número entero positivo y considere

Cuando x → ∞,  f (x) → 0  y  g (x) → ∞. Sin embargo, el límite cuando x → ∞  de  

varía, dependiendo de n. Si n = 2, entonces lim _{x → ∞} f (x) / g (x) = 3. Si n = 1, entonces lim _{x →} f (x) / g (x) = ∞. Si n = 3, entonces lim _{x → ∞} f (x) / g (x) = 0.

Forma indeterminada de tipo ∞ − ∞

Otro tipo de forma indeterminada es ∞ − ∞. Considere el siguiente ejemplo. Sea n un número entero positivo y sea f (x) = 3xⁿ  y  g (x) = 3x² + 5. Cuando x → ∞, f (x) → ∞  y  g (x) → ∞. Estamos interesados en lim _{x → ∞} (f (x) − g (x)). Dependiendo de si f (x) crece más rápido, g (x) crece más rápido o crecen a la misma velocidad, como vemos a continuación, cualquier cosa puede suceder en este límite. Dado que f (x) → ∞  y  g (x) → ∞, escribimos ∞ − ∞ para denotar la forma de este límite. Al igual que con nuestras otras formas indeterminadas, ∞ − ∞ no tiene significado por sí solo y debemos hacer más análisis para determinar el valor del límite. Por ejemplo, suponga que el exponente n en la función f (x) = 3xⁿ  es n = 3, entonces

Por otro lado, si n = 2, entonces

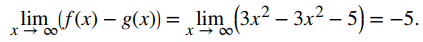
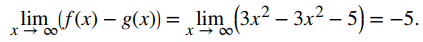
Sin embargo, si n = 1, entonces

Otro tipo de forma indeterminada que surge al evaluar los límites involucra exponentes.

Formas indeterminadas 0⁰, ∞⁰ y 1^∞

Las expresiones 0⁰, ∞⁰ y 1^∞ son todas formas indeterminadas. Por sí solas, estas expresiones no tienen sentido porque en realidad no podemos evaluar estas expresiones como evaluaríamos una expresión que involucra números reales. Más bien, estas expresiones representan formas que surgen al encontrar límites. En los videos para los “Ejercicios resueltos” de esta sección examinamos cómo se puede usar la regla de L’Hôpital para evaluar los límites que involucran estas formas indeterminadas.

Dado que la regla de L’Hôpital se aplica a los cocientes, utilizamos la función de logaritmo natural y sus propiedades para reducir un problema al evaluar un límite que involucra exponentes a un problema relacionado que involucra un límite de un cociente.

Por ejemplo, supongamos que queremos evaluar lim _{x → a} f (x) ^{g (x)} y llegamos a la forma indeterminada ∞⁰.

(Las formas indeterminadas 0⁰ y 1^∞ pueden manejarse de manera similar.)

Procedemos de la siguiente manera.

Sea

Entonces,

Por lo tanto

Como lim _{x → a} f (x) = ∞, sabemos que lim _{x → a} ln (f (x)) = ∞. Por lo tanto, lim _{x → a} g (x) ln (f (x)) es de la forma indeterminada 0⋅∞, y podemos usar las técnicas discutidas anteriormente para reescribir la expresión g (x) ln (f (x)) en una forma para que podamos aplicar la regla de L’Hôpital.

Supongamos que lim _{x → a} g (x) ln (f (x))  = L, donde L puede ser ∞ o −∞. Luego

Como la función de logaritmo natural es continua, concluimos que

lo que nos da

Ejercicios resueltos