(5. LA INTEGRAL Y TÉCNICAS DE INTEGRACIÓN)
(5.13 Integración numérica)
Regla de Simpson
Con la regla del punto medio, estimamos áreas de regiones bajo curvas usando rectángulos. En cierto sentido, aproximamos la curva con funciones constantes por partes. Con la regla trapezoidal, aproximamos la curva usando funciones lineales por partes. ¿Qué pasaría si, en cambio, tuviéramos que aproximar una curva usando funciones cuadráticas por partes? Con la regla de Simpson, hacemos precisamente esto. Dividimos el intervalo en un número par de subintervalos, cada uno de igual ancho. Sobre el primer par de subintervalos aproximamos
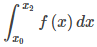
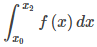
con
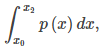
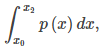
donde p(x) = Ax² + Bx + C es la función cuadrática que pasa por (x₀, f (x₀)), (x₁, f (x₁)) y (x₂, f (x₂)) (Figura 5.13_4).
Sobre el siguiente par de subintervalos aproximamos
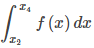
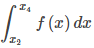
con la integral de otra función cuadrática pasando por (x₂, f (x₂)), (x₃, f (x₃)) y (x₄, f (x₄)). Este proceso continúa con cada par sucesivo de subintervalos.
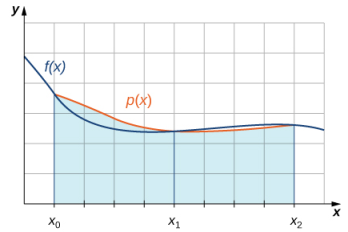
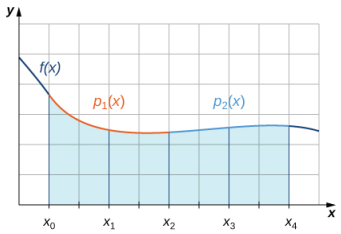
(Figura 5.13_4 Con la regla de Simpson, aproximamos una integral definida integrando una función cuadrática por partes.)
Para comprender la fórmula que obtenemos para la regla de Simpson, comenzamos por deducir una fórmula para esta aproximación en los dos primeros subintervalos. A medida que avanzamos en la deducción, debemos tener en cuenta las siguientes relaciones:
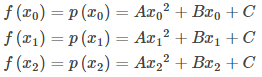
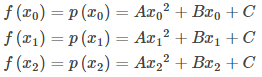
x₂ − x₀ = 2Δx, donde Δx es la longitud de un subintervalo.
x₂ + x₀ = 2x₁, ya que x₁ = (x₂ + x₀)/2.
Así,
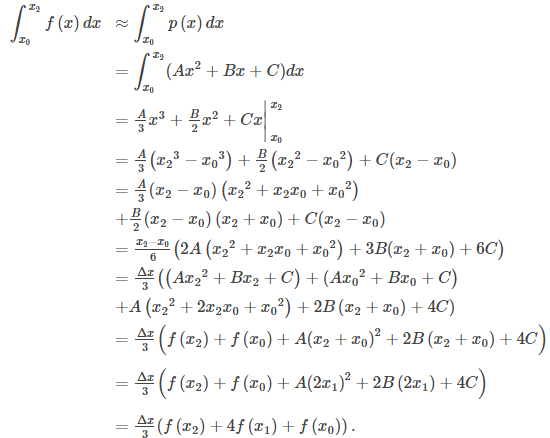
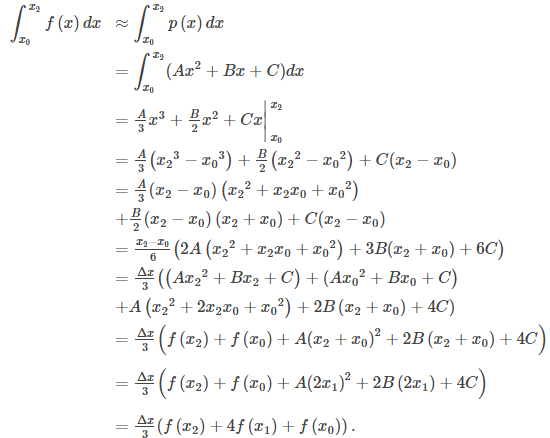
Si aproximamos
usando el mismo método, obtenemos
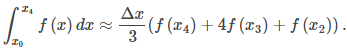
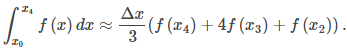
Combinando estas dos aproximaciones, obtenemos
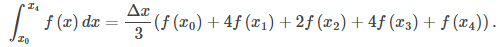
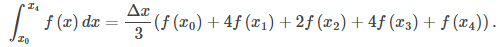
El patrón continúa a medida que agregamos pares de subintervalos a nuestra aproximación. La regla general puede establecerse de la siguiente manera.
TEOREMA 5.13_4. Regla de Simpson
|
Suponga que f (x) es continua sobre el intervalo cerrado [a, b]. Sea n un entero par positivo y Δx = (b − a)/n. Se divide [a, b] en n subintervalos, cada uno de longitud Δx, con puntos finales en P = {x₀, x₁, x₂,…, xn}. Ya que
Entonces |
Así como la regla trapezoidal es el promedio de las reglas de la izquierda y la derecha para estimar integrales definidas, la regla de Simpson se puede obtener a partir de las reglas del punto medio y trapezoidal usando un promedio ponderado. Se puede demostrar que S2n = (2/3)Mn + (1/3)Tn.
También es posible poner un límite al error cuando se usa la regla de Simpson para aproximar una integral definida. El límite en el error viene dado por la siguiente regla:
REGLA: ERROR conexo A LA REGLA DE SIMPSON
Sea f (x) una función continua sobre [a, b] que tiene una cuarta derivada, durante este intervalo. Si M es el valor máximo de sobre [a, b], entonces el límite superior del error al usar Sn para estimar está dado por |
EJEMPLO ILUSTRATIVO 5.13_7. Aplicación de la regla de Simpson_1
Utilice S₂ para aproximar
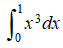
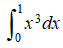
Estime un límite para el error en S₂.
Solución:
Dado que [0, 1] se divide en dos intervalos, cada subintervalo tiene una longitud Δx = (1− 0)/2 = 1/2. Los puntos finales de estos subintervalos son {0, 1/2, 1}. Si establecemos f (x) = x³, entonces
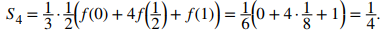
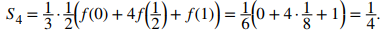
Dado que f ⁽⁴⁾(x) = 0 y consecuentemente M = 0, vemos que
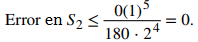
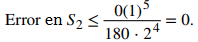
Este límite indica que el valor obtenido mediante la regla de Simpson es exacto. Una revisión rápida verificará que, de hecho,
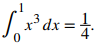
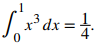
EJEMPLO ILUSTRATIVO 5.13_8. Aplicación de la regla de Simpson_2
Utilice S₆ para estimar la longitud de la curva y = (1/2)x² sobre [1, 4].
Solución:
La longitud de y = (1/2)x² sobre [1, 4] es
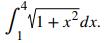
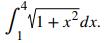
Si dividimos [1, 4] en seis subintervalos, entonces cada subintervalo tiene una longitud Δx = (4 − 1)/6 = 1/2, y los puntos finales de los subintervalos son {1, 3/2, 2, 5/2, 3, 7/2, 4}. Configurando f (x) = √(1 + x²),
Después de sustituir, obtenemos
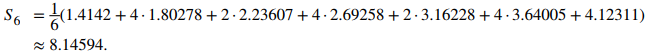
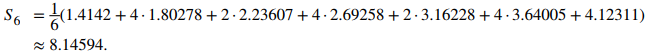
Ejercicio de control 5.13_5
Utilice S₂ para estimar
