(5. LA INTEGRAL Y TÉCNICAS DE INTEGRACIÓN)
(5.13 Integración numérica)
Error absoluto y error relativo
Un aspecto importante del uso de estas reglas de aproximación numérica consiste en calcular el error al usarlas para estimar el valor de una integral definida. Primero necesitamos definir el error absoluto y el error relativo.
DEFINICIÓN
|
Si B es nuestra estimación de alguna cantidad que tiene un valor real de A, entonces el error absoluto viene dado por |A − B|. El error relativo es el error como porcentaje del valor absoluto y está dado por |(A − B)/A| = |(A − B)/A|⋅100%. |
EJEMPLO ILUSTRATIVO 5.13_4. Calcular el error en la regla del punto medio
Calcule el error absoluto y relativo en la estimación de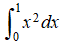
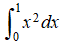
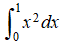
utilizando la regla del punto medio.
Solución:
El valor exacto de esta integral es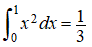
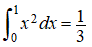
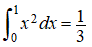
y la estimación que hicimos en el Ejemplo ilustrativo 5.13_1 es M₄ = 21/64. Por lo tanto, el error absoluto está dado por |1/3 − 21/64| = 1/192 ≈ 0,0052. El error relativo es
EJEMPLO ILUSTRATIVO 5.13_5. Calculando el error en la regla trapezoidal
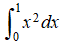
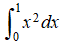
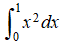
Calcule el error absoluto y relativo en la estimación deutilizando la regla del trapecio.
Solución:
El valor exacto de esta integral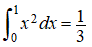
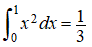
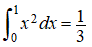
y la estimación que hicimos en el Ejemplo ilustrativo 5.13_3 es T₄ = 11/32. Por lo tanto, el error absoluto viene dado por |1/3 − 11/32|= 1/96 ≈ 0.0104. El error relativo viene dado por
Ejercicio de control 5.13_3
En un punto de control anterior, estimamos que
era 24/35 usando T₂. El valor exacto de esta integral es ln2. Usando 24/35 ≈ 0,6857 y ln2 ≈ 0,6931, calcule el error absoluto y el error relativo.
En los dos ejemplos anteriores, pudimos comparar nuestra estimación de una integral con el valor exacto de la integral; sin embargo, normalmente no tenemos este lujo. En general, si estamos aproximando una integral, lo hacemos porque no podemos calcular fácilmente el valor exacto de la integral en sí. Por lo tanto, a menudo es útil poder determinar un límite superior para el error en una aproximación de una integral. El siguiente teorema proporciona límites de error para las reglas del punto medio y trapezoidal. El teorema se establece sin prueba.
TEOREMA 5.13_3. Límites de error para las reglas del punto medio y trapezoidal
|
Sea f (x) una función continua sobre [a, b], que tiene una segunda derivada f ″(x) sobre este intervalo. Si M es el valor máximo de | f ″(x)| sobre [a, b], entonces los límites superiores del error al usar Mn y Tn para estimar
y
|
son
Podemos usar estos límites para determinar el valor de n necesario para garantizar que el error en una estimación sea menor que un valor especificado.
EJEMPLO ILUSTRATIVO 5.13_6. Determinación del número de intervalos a utilizar
¿Qué valor de n debe usarse para garantizar que una estimación de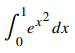
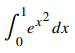
sea precisa dentro de 0.01 si usamos la regla del punto medio?
Solución:
Comenzamos determinando el valor de M, el valor máximo de | f ” (x)| en el intervalo [0, 1] para
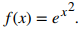
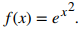
Ya que
tenemos que
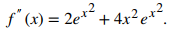
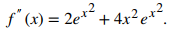
Así,
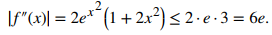
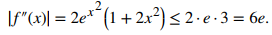
De la fórmula dada en el TEOREMA 5.13_3 para estimar del error al aplicar la regla del punto medio, se tiene que
Ahora resolvemos la siguiente desigualdad para n:
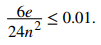
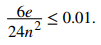
Así,
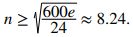
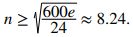
Dado que n debe ser un número entero que satisface esta desigualdad, una elección de n = 9 garantiza que
Análisis
Podríamos haber tenido la tentación de redondear 8,24 hacia abajo y elegir n = 8, pero esto sería incorrecto porque debemos tener un número entero mayor o igual que 8,24. Debemos tener en cuenta que las estimaciones de error proporcionan un límite superior solo para el error. De hecho, la estimación real puede ser una aproximación mucho mejor que la indicada por el límite de error.
Ejercicio de control 5.13_4
Use la Ecuación
para encontrar un límite superior para el error al usar M₄ para estimar