(5. LA INTEGRAL Y TÉCNICAS DE INTEGRACIÓN)
(5.13 Integración numérica)
La regla trapezoidal
También podemos aproximar el valor de una integral definida usando trapezoides en lugar de rectángulos. En la Figura 5.13_2, el área bajo la curva se aproxima mediante trapezoides en lugar de rectángulos.

La regla trapezoidal para estimar integrales definidas usa trapezoides en lugar de rectángulos para aproximar el área bajo una curva. Para comprender mejor la forma final de la regla, considere los trapecios que se muestran en la Figura 5.13._2. Suponemos que la longitud de cada subintervalo está dada por Δx. Primero, recuerde que el área de un trapezoide con una altura h y bases de longitud b₁ y b₂ está dada por Área = (1/2)h(b₁ + b₂). Vemos que el primer trapezoide tiene una altura Δx y bases paralelas de longitud f (x₀) y f (x₁). Por tanto, el área del primer trapezoide de la figura 5.13._2 es


Las áreas de los tres trapezoides restantes son


Por consiguiente,


Después de sacar un factor común de (1/2)Δx y combinar términos semejantes, tenemos
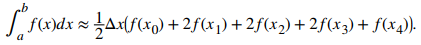
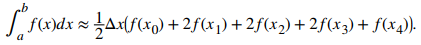
Generalizando, declaramos formalmente la siguiente regla.
TEOREMA 5.13_2. La regla trapezoidal
Suponga que f (x) es continua sobre [a, b]. Sea n un número entero positivo y Δx = (b − a)/n. Sea [a, b] dividido en n subintervalos, cada uno de longitud Δx, con puntos finales en P = {x₀, x₁, x₂…, xn}. Dado que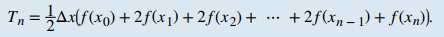 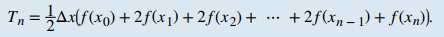   |
Antes de continuar, hagamos algunas observaciones sobre la regla trapezoidal. En primer lugar, es útil señalar que


donde


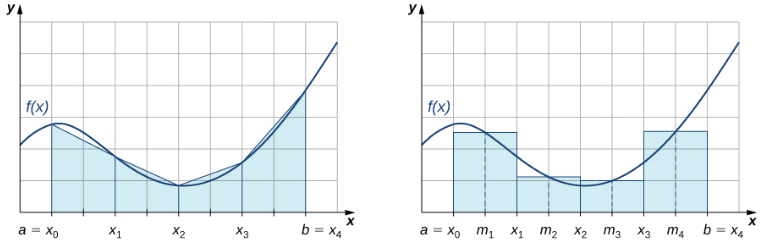
Es decir, Ln y Rn se aproximan a la integral utilizando los puntos extremos izquierdo y derecho de cada subintervalo, respectivamente. Además, un examen cuidadoso de la figura 5.13_3 nos lleva a hacer las siguientes observaciones sobre el uso de las reglas trapezoidales y las reglas del punto medio para estimar la integral definida de una función no negativa. La regla trapezoidal tiende a sobrestimar sistemáticamente el valor de una integral definida en intervalos donde la función es cóncava hacia arriba y a subestimar el valor de una integral definida de forma sistemática en intervalos donde la función es cóncava hacia abajo. Por otro lado, la regla del punto medio tiende a promediar estos errores de alguna manera al sobreestimar parcialmente y subestimar parcialmente el valor de la integral definida en estos mismos tipos de intervalos. Esto nos lleva a plantear la hipótesis de que, en general, la regla del punto medio tiende a ser más precisa que la regla trapezoidal.

EJEMPLO ILUSTRATIVO 5.13_3. Usando la regla trapezoidal
Use la regla trapezoidal para estimar

Solución:
Los puntos finales de los subintervalos constan de elementos del conjunto P = {0, 1/4, 1/2, 3/4, 1} y Δx = (1 − 0)/4 = 1/4. Así,


Ejercicio de control 5.13_2
Utilice la regla trapezoidal con n = 2 para estimar


