El producto punto | Calculo21

(Cálculo vectorial)

Vectores ortogonales

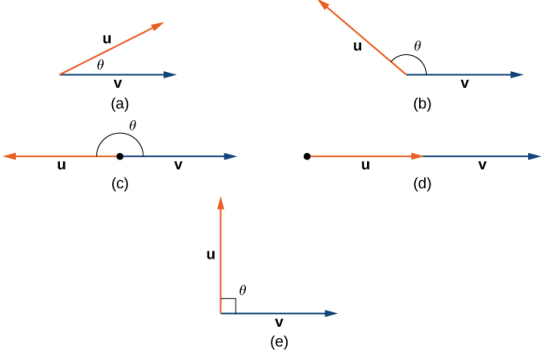
El ángulo entre dos vectores puede ser agudo (0 < cosθ < 1), obtuso (−1 < cosθ < 0) o recto (cosθ = −1). Si cosθ = 1, ambos vectores tienen la misma dirección. Si cosθ = 0, entonces los vectores, cuando se colocan en posición estándar, forman un ángulo recto (Figura 10.3_3). Podemos formalizar este resultado en un teorema con respecto a los vectores ortogonales (perpendiculares).

**Figura 10.3_3** (a) Un ángulo agudo tiene 0 < cosθ < 1. (b) Un ángulo obtuso tiene −1 < cosθ < 0. (c) Una línea recta tiene cosθ = −1. (d) Si los vectores tienen la misma dirección, cosθ = 1. (e) Si los vectores son ortogonales (perpendiculares), cosθ = 0.

TEOREMA 10.3.3. Vectores ortogonales

Los vectores distintos de cero u y v son vectores ortogonales si y sólo si

u ⋅ v = 0.

Prueba

Supongamos que u y v son vectores distintos de cero y que θ denota el ángulo entre ellos. Primero, suponga que u⋅v = 0. Luego

∥u∥∥v∥cosθ = 0.

Sin embargo, ∥u∥ ≠ 0 y ∥v∥ ≠ 0, por lo que debemos tener cosθ = 0. Por lo tanto, θ = 90 °, y los vectores son ortogonales.

Ahora suponga que u y v son ortogonales. Entonces θ = 90 ° y tenemos

u⋅v = ∥u∥∥v∥cosθ = ∥u∥∥v∥cos90° = ∥u∥∥v∥ (0) = 0.

Los términos ortogonal, perpendicular y normal indican que los objetos matemáticos se cortan en ángulo recto. El uso de cada término está determinado principalmente por su contexto. Decimos que los vectores son ortogonales y las rectas son perpendiculares. El término normal se usa con mayor frecuencia cuando se mide el ángulo hecho con un plano u otra superficie.

EJEMPLO ILUSTRATIVO 10.3_3. Identificación de vectores ortogonales

Determine si p = ⟨1, 0, 5⟩ y q = ⟨10, 3, −2⟩ son vectores ortogonales.

Solución:

Usando la definición, solo necesitamos verificar el producto punto de los vectores:

p⋅q = 1 (10) + (0) (3) + (5) (- 2) = 10 + 0 − 10 = 0.

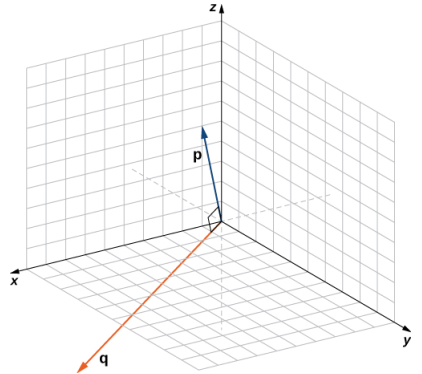
Como p⋅q = 0, los vectores son ortogonales (figura 10.3_4).

**Figura 10.3_4** Los vectores p y q forman un ángulo recto cuando sus puntos iniciales están alineados.

Ejercicio de control 10.3_4

¿Para qué valor de x es p = ⟨2, 8, −1⟩ ortogonal a q = ⟨x, −1, 2⟩?

EJEMPLO ILUSTRATIVO 10.3_4. Medición del ángulo formado por dos vectores

Sea v = ⟨2, 3, 3⟩. Encuentra las medidas de los ángulos formados por los siguientes vectores.
a) v e i
b) v y j
c) v y k

Solución:
a) Sea α el ángulo formado por v e i:

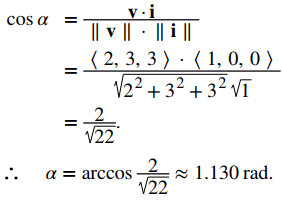
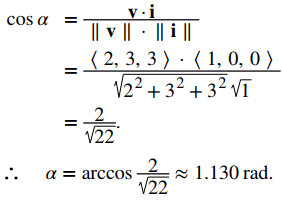
b) Supongamos que β representa el ángulo formado por v y j:

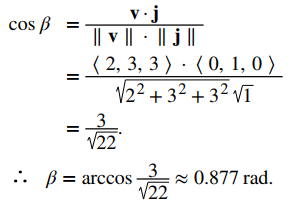
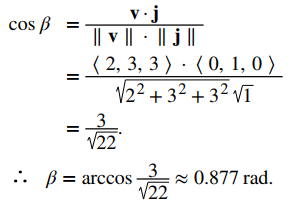
c) Deje γ representar el ángulo formado por v y k:

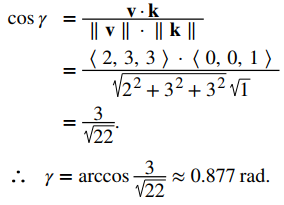
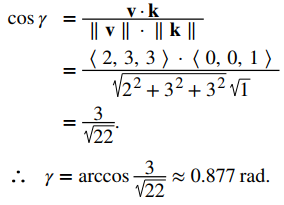
Ejercicio de control 10.3_5

Sea v = ⟨3, −5, 1⟩. Calcula la medida de los ángulos formados por cada par de vectores.

v y i
v y j
v y k

El ángulo que forma un vector con cada uno de los ejes de coordenadas, llamado ángulo de dirección, es muy importante en los cálculos prácticos, especialmente en un campo como la ingeniería. Por ejemplo, en ingeniería astronáutica, el ángulo en el que se lanza un cohete debe determinarse con mucha precisión. Un error muy pequeño en el ángulo puede hacer que el cohete se desplace cientos de millas. Los ángulos de dirección a menudo se calculan utilizando el producto escalar y los cosenos de los ángulos, llamados cosenos de dirección. Por lo tanto, definimos ambos ángulos y sus cosenos.

Definición. Ángulos y cosenos de dirección

Los ángulos formados por un vector distinto de cero y los ejes de coordenadas se denominan ángulos de dirección para el vector (Figura 10.3_5). Los cosenos para estos ángulos se denominan cosenos de dirección.

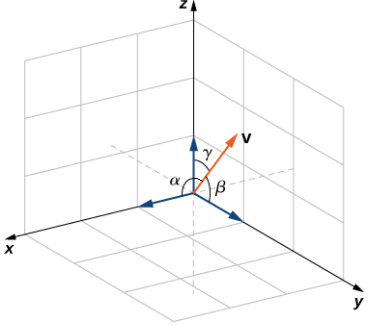
**Figura 10.3_5** El ángulo α está formado por el vector v y el vector unitario i. El ángulo β está formado por el vector v y el vector unitario j. El ángulo γ está formado por el vector v y el vector unitario k.

En el ejemplo 10.3_4, los cosenos de dirección de v = ⟨2, 3, 3⟩ son cosα = 2/√22, cosβ = 3/√22 y cosγ = 3/√22. Los ángulos de dirección de v son α = 1.130 rad, β = 0.877 rad y γ = 0.877 rad.

Hasta ahora, nos hemos centrado principalmente en vectores relacionados con la fuerza, el movimiento y la posición en el espacio físico tridimensional. Sin embargo, los vectores a menudo se usan de formas más abstractas. Por ejemplo, supongamos que un vendedor de frutas vende manzanas, plátanos y naranjas. En un día determinado, vende 30 manzanas, 12 plátanos y 18 naranjas. Podría usar un vector de cantidad, q = ⟨30, 12, 18⟩, para representar la cantidad de fruta que vendió ese día. De manera similar, podría usar un vector de precios, p = ⟨0.50, 0.25, 1⟩, para indicar que vende sus manzanas por 50¢ cada una, plátanos por 25¢ cada uno y naranjas por $1 cada una. En este ejemplo, aunque todavía podríamos graficar estos vectores, no los interpretamos como representaciones literales de posición en el mundo físico. Simplemente estamos usando vectores para realizar un seguimiento de piezas particulares de información sobre manzanas, plátanos y naranjas.

Esta idea puede parecer un poco extraña, pero si simplemente consideramos los vectores como una forma de ordenar y almacenar datos, descubriremos que pueden ser una herramienta bastante poderosa. Volviendo al vendedor de frutas, pensemos en el producto escalar, q ⋅ p. Lo calculamos multiplicando la cantidad de manzanas vendidas (30) por el precio por manzana (50¢), la cantidad de bananas vendidas por el precio de la banana y la cantidad de naranjas vendidas por el precio de la naranja. Luego sumamos todos estos valores. Entonces, en este ejemplo, el producto punto nos dice cuánto dinero tenía el vendedor de frutas en ventas ese día en particular.

Cuando usamos vectores de esta manera más general, no hay razón para limitar el número de componentes a tres. ¿Qué pasa si el vendedor de fruta decide comenzar a vender toronja? En ese caso, le gustaría usar vectores de cantidad y precio de cuatro dimensiones para representar la cantidad de manzanas, plátanos, naranjas y toronjas vendidas, y sus precios unitarios. Como es de esperar, para calcular el producto escalar de los vectores de cuatro dimensiones, simplemente agregamos los productos de los componentes como antes, pero la suma tiene cuatro términos en lugar de tres.

EJEMPLO ILUSTRATIVO 10.3_5. Usando vectores en un contexto económico

AAA Party Supply Store vende invitaciones, recuerdos de fiesta, decoraciones y artículos para el servicio de alimentos como platos de papel y servilletas. Cuando AAA compra su inventario, paga 25 ¢ por paquete por invitaciones y recuerdos de fiesta. Las decoraciones cuestan 50 ¢ cada una, y los artículos de servicio de comida cuestan 20 ¢ por paquete. AAA vende invitaciones a $ 2.50 por paquete y recuerdos de fiesta a $ 1.50 por paquete. Las decoraciones se venden por $ 4.50 cada una y los artículos de servicio de comida a $ 1.25 por paquete.
Durante el mes de mayo, AAA Party Supply Store vende 1258 invitaciones, 342 recuerdos de fiesta, 2426 decoraciones y 1354 artículos de servicio de alimentos. Use vectores y el producto de punto para calcular cuánto dinero ganó AAA en ventas durante el mes de mayo. ¿Cuánto hizo la tienda en ganancias?

Solución:

Los vectores de costo, precio de venta y cantidad son

Las ventas de AAA para el mes de mayo se pueden calcular utilizando el producto punto p⋅q. Tenemos

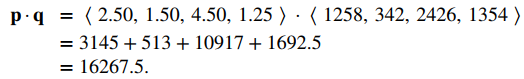
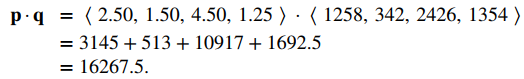
Entonces, AAA recibió $ 16,267.50 durante el mes de mayo.

Para calcular la ganancia, primero debemos calcular cuánto pagó AAA por los artículos vendidos. Usamos el producto punto c⋅q para obtener

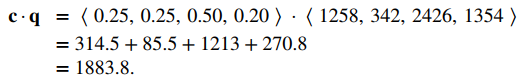
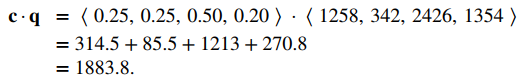
Entonces, AAA pagó $ 1,883.80 por los artículos que vendieron. Su beneficio, entonces, está dado por

Por lo tanto, AAA Party Supply Store ganó $ 14.383,70 en mayo.

Páginas: 1 2 3