Proyecciones vectoriales
Como hemos visto, la suma combina dos vectores para crear un vector resultante. Pero, ¿qué pasa si se nos da un vector y necesitamos encontrar sus partes componentes? Utilizamos proyecciones vectoriales para realizar el proceso opuesto; pueden descomponer un vector en sus componentes. La magnitud de una proyección vectorial es una proyección escalar. Por ejemplo, si un niño tira del mango de un vagón en un ángulo de 55 °, podemos usar proyecciones para determinar cuánta fuerza sobre el mango está moviendo el vagón hacia adelante (Figura 10.3_5). Volvemos a este ejemplo y aprendemos cómo resolverlo después de ver cómo calcular las proyecciones.

Definición. Proyección vectorialLa proyección vectorial de v sobre u es el vector marcado projᵤv en la figura 10.3_7. Tiene el mismo punto inicial que u y v y la misma dirección que u, y representa el componente de v que actúa en la dirección de u. Si θ representa el ángulo entre u y v, entonces, por las propiedades de los triángulos, sabemos que la longitud de projᵤv es ∥ projᵤv ∥ = ∥v∥cosθ. Al expresar cosθ en términos del producto escalar, esto se convierte en
Ahora multiplicamos por un vector unitario en la dirección de u para obtener projᵤv:
La longitud de este vector también se conoce como la proyección escalar de v sobre u y se denota por
|


EJEMPLO ILUSTRATIVO 10.3_6. Encontrar proyecciones
Encuentre la proyección de v sobre u.
a) v = ⟨3, 5, 1⟩ y u = ⟨− 1, 4, 3⟩
b) v = 3i − 2j y u = i + 6j
Solución:
a) Sustituya los componentes de v y u en la fórmula para la proyección:


b) Para encontrar la proyección bidimensional, simplemente adapte la fórmula al caso bidimensional:
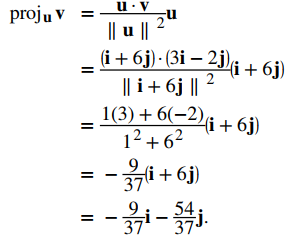
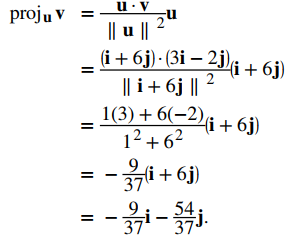
A veces es útil descomponer vectores, es decir, separar un vector en una suma. Este proceso se llama resolución de un vector en componentes. Las proyecciones nos permiten identificar dos vectores ortogonales que tienen una suma deseada. Por ejemplo, sea v = ⟨6, −4⟩ y sea u = ⟨3, 1⟩. Queremos descomponer el vector v en componentes ortogonales de modo que uno de los vectores componentes tenga la misma dirección que u.
Primero encontramos el componente que tiene la misma dirección que u proyectando v sobre u. Deje p = projᵤv. Entonces tenemos


Ahora considere el vector q = v − p. Tenemos


Claramente, por la forma en que definimos q, tenemos v = q + p, y


Por lo tanto, q y p son ortogonales.
EJEMPLO ILUSTRATIVO 10.3_7. Resolviendo vectores en componentes
Exprese v = ⟨8, −3, −3⟩ como una suma de vectores ortogonales de modo que uno de los vectores tenga la misma dirección que u = ⟨2, 3, 2⟩.
Solución:
Supongamos que p representa la proyección de v sobre u:


Entonces,


Para verificar nuestro trabajo, podemos usar el producto punto para verificar que p y q son vectores ortogonales:


Luego,


EJEMPLO ILUSTRATIVO 10.3_8. Proyección Escalar de Velocidad
Un barco de contenedores sale del puerto y viaja 15° al norte del este. Su motor genera una velocidad de 20 nudos a lo largo de ese camino (ver la siguiente figura). Además, la corriente oceánica mueve el barco hacia el noreste a una velocidad de 2 nudos. Considerando tanto el motor como la corriente, ¿qué tan rápido se mueve el barco en la dirección 15° al norte del este? Redondea la respuesta a dos decimales.


Solución:
Sea v el vector de velocidad generado por el motor, y sea w el vector de velocidad de la corriente. Ya sabemos ∥v∥ = 20 a lo largo de la ruta deseada. Solo necesitamos agregar la proyección escalar de w en v. Obtenemos


El barco se mueve a 21.73 nudos en la dirección 15° al norte del este.
Trabajo
Ahora que entendemos los productos punto, podemos ver cómo aplicarlos a situaciones de la vida real. La aplicación más común del producto escalar de dos vectores está en el cálculo del trabajo.
Por física, sabemos que el trabajo se realiza cuando un objeto es movido por una fuerza. Cuando la fuerza es constante y se aplica en la misma dirección en que se mueve el objeto, definimos el trabajo realizado como el producto de la fuerza y la distancia que recorre el objeto: W = Fd. Vimos varios ejemplos de este tipo en capítulos anteriores. Ahora imagine que la dirección de la fuerza es diferente de la dirección del movimiento, como en el ejemplo de un niño que tira de un carro. Para encontrar el trabajo realizado, necesitamos multiplicar el componente de la fuerza que actúa en la dirección del movimiento por la magnitud del desplazamiento. El producto punto nos permite hacer precisamente eso. Si representamos una fuerza aplicada por un vector F y el desplazamiento de un objeto por un vector s, entonces el trabajo realizado por la fuerza es el producto escalar de F y s.
Definición. TrabajoCuando se aplica una fuerza constante a un objeto para que el objeto se mueva en línea recta desde el punto P al punto Q, el trabajo W realizado por la fuerza F, que actúa en un ángulo θ desde la línea de movimiento, viene dado por
|
Volvamos al problema del carro del niño presentado anteriormente. Supongamos que un niño tira de un carro con una fuerza que tiene una magnitud de 8 lb sobre el mango en un ángulo de 55°. Si el niño tira de la carreta 50 pies, encuentre el trabajo realizado por la fuerza (Figura 10.3_8).


Figura 10.3_8 El componente horizontal de la fuerza es la proyección de F sobre el eje x positivo.
Nosotros tenemos


En unidades estándar de EE. UU., Medimos la magnitud de la fuerza ∥F∥ en libras. La magnitud del vector de desplazamiento.


nos dice qué tan lejos se movió el objeto, y se mide en pies. La unidad de medida habitual para el trabajo, entonces, es la libra-pie. Una libra de pie es la cantidad de trabajo requerida para mover un objeto que pesa 1 libra a una distancia de 1 pie hacia arriba. En el sistema métrico, la unidad de medida de la fuerza es el newton (N), y la unidad de medida de magnitud para el trabajo es un newton-metro (N · m), o un julio (J).
EJEMPLO ILUSTRATIVO 10.3_9. Cálculo de Trabajo
Una cinta transportadora genera una fuerza F = 5i − 3j + k que mueve una maleta desde el punto (1, 1, 1) al punto (9, 4,7 ) a lo largo de una línea recta. Encuentra el trabajo realizado por la cinta transportadora. La distancia se mide en metros y la fuerza se mide en newtons.
Solución:



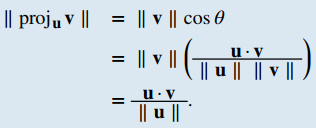
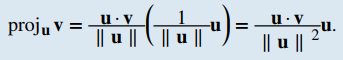
Great content! Super high-quality! Keep it up! 🙂