Álgebra lineal con aplicaciones

| 1. Sistema de ecuaciones lineales |

Ejercicios complementarios del capítulo 1

 

1. En el capítulo 4 mostramos que la gráfica de una ecuación ax + by + cz = d es un plano en el espacio cuando no todos los coeficientes a, b y c son cero.

a. Al examinar las posibles posiciones de los planos en el espacio, demuestre que tres ecuaciones en tres variables pueden tener cero, una o infinitas soluciones.
b. ¿Pueden dos ecuaciones en tres variables tener una solución única? Justifica tu respuesta.

 

2. Encuentre todas las soluciones de los siguientes sistemas de ecuaciones lineales.

 

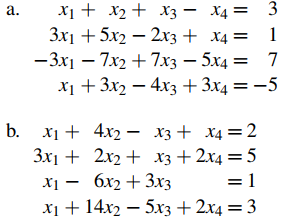
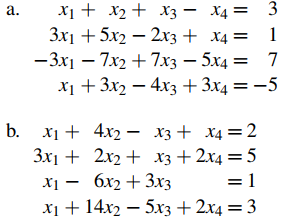
3. En cada caso, encuentre (si es posible) condiciones en a, b y c tales que el sistema tenga cero, una o infinitas soluciones.

 

4. Demuestre que dos filas cualesquiera de una matriz pueden intercambiarse mediante transformaciones de filas elementales de los otros dos tipos.

 

5. Si ad ≠ bc, demuestre que tiene una forma escalonada reducida

 

6. Encuentre a, b y c de modo que el sistematenga la solución x = 3, y = −1, z = 2.

 

7. Resuelve el sistemadonde i² = −1. [Ver Apéndice A.]

 

8. Demuestre que el sistema realtiene una solución compleja: x = 2, y = i, z = 3 – i donde i2 = −1. Explicar. ¿Qué sucede cuando un sistema real semejante tiene una solución única?

 

9. El médico le indica a un hombre que tome 5 unidades de vitamina A, 13 unidades de vitamina B y 23 unidades de vitamina C al día. Hay tres marcas de píldoras de vitaminas disponibles y la cantidad de unidades de cada vitamina por píldora se muestra en la tabla adjunta.

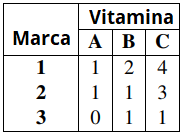
a. Encuentre todas las combinaciones de píldoras que proporcionen exactamente la cantidad requerida de vitaminas (no se permiten píldoras parciales).
b. Si las marcas 1, 2 y 3 cuestan 3 ¢, 2 ¢ y 5 ¢ por pastilla, respectivamente, busque el tratamiento menos costoso.

 

10. El dueño de un restaurante planea usar x mesas con capacidad para 4, y mesas con capacidad para 6 y z mesas con capacidad para 8, para un total de 20 mesas. Cuando están completamente ocupadas, las mesas tienen capacidad para 108 clientes. Si solo se utilizan la mitad de las mesas x, la mitad de las mesas y y la cuarta parte de las mesas z, cada una completamente ocupada, entonces 46 clientes se sentarán. Encuentre x, y y z.

 

11. a. Muestre que una matriz con dos filas y dos columnas que está en forma escalonada reducida debe tener una de las siguientes formas:

[Sugerencia: el 1 inicial en la primera fila debe estar en la columna 1 o 2 o no existir].

b. Enumere las siete formas escalonadas de filas reducidas para matrices con dos filas y tres columnas.
c. Enumere las cuatro formas escalonadas de filas reducidas para matrices con tres filas y dos columnas.

 

12. Un parque de diversiones cobra $ 7 para adultos, $ 2 para jóvenes y $ 0.50 para niños. Si entran 150 personas y pagan un total de $ 100, encuentre el número de adultos, jóvenes y niños. [Sugerencia: estos números son números enteros no negativos].

 

13. Resuelve el siguiente sistema de ecuaciones para x e y.

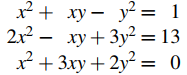
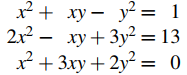
[Sugerencia: estas ecuaciones son lineales en las nuevas variables x₁ = x², x₂ = xy y x₃ = y².]