Álgebra lineal con aplicaciones
| 1. Sistema de ecuaciones lineales | Ejercicios propuestos para el Capítulo 1.5 |
1.5 Una aplicación a las redes eléctricas
En una red eléctrica, a menudo es necesario encontrar la corriente en amperios (A) que fluye en varias partes de la red. Estas redes suelen contener resistencias que retardan la corriente. Las resistencias se indican con un símbolo (



Ley de Ohm
La corriente I y la caída de voltaje V a través de una resistencia R están relacionadas por la ecuación V = RI. ◊
Leyes de Kirchhoff
1. (Regla de la unión) El flujo de corriente hacia una unión es igual al flujo de corriente que sale de esa unión.
2. (Regla del circuito) La suma algebraica de las caídas de voltaje (debido a resistencias) alrededor de cualquier circuito cerrado de la red debe ser igual a la suma de los aumentos de voltaje alrededor del circuito. ◊
Al aplicar la regla 2, seleccione una dirección (en sentido horario o antihorario) alrededor del circuito cerrado y luego considere todos los voltajes y corrientes positivos cuando están en esta dirección y negativos cuando están en la dirección opuesta. Por eso se usa el término suma algebraica en la regla 2. Aquí hay un ejemplo.
Ejemplo ilustrativo 1.4_1
Encuentre las diversas corrientes en el circuito que se muestra en el siguiente diagrama.
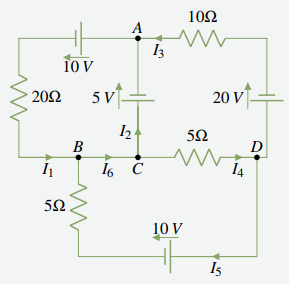
Solución:
Primero aplique la regla de unión en las uniones A, B, C y D para obtener
Unión A I1 = I2 + I3
Unión B I6 = I1 + I5
Unión C I2 + I4 = I6
Unión D I3 + I5 = I4
Tenga en cuenta que estas ecuaciones no son independientes (de hecho, la tercera es una consecuencia fácil de las otras tres).
A continuación, la regla del circuito insiste en que la suma de los aumentos de voltaje (debido a las fuentes) alrededor de un circuito cerrado debe ser igual a la suma de las caídas de voltaje (debido a las resistencias). Según la ley de Ohm, la pérdida de voltaje a través de una resistencia R (en la dirección de la corriente I) es RI. Ir en sentido antihorario alrededor de tres circuitos cerrados produce
Arriba a la izquierda 10 + 5 = 20I1
Arriba a la derecha −5 + 20 = 10I3 + 5I4
Inferior −10 = −5I5 − 5I4
Por tanto, sin tener en cuenta la ecuación redundante obtenida en la unión C, tenemos seis ecuaciones en las seis incógnitas I1, …, I6. La solución es

El hecho de que I2 sea negativo significa, por supuesto, que esta corriente está en la dirección opuesta, con una magnitud de 1/20 amperios.
Ejercicios propuestos para el capítulo 1.5
En los Ejercicios 1 a 4, encuentre las corrientes en los circuitos.
1. 

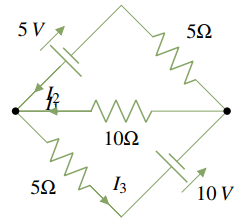

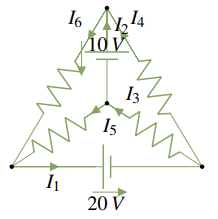
3. 


5. Encuentre el voltaje x tal que la corriente I1 = 0.