Álgebra lineal con aplicaciones
| 1. Sistema de ecuaciones lineales | Ejercicios propuestos para el Capítulo 1.4 |
1.4 Una aplicación para el flujo de red
Hay muchos tipos de problemas que afectan a una red de conductores a lo largo de la cual se observa algún tipo de flujo. Ejemplos de estos incluyen una red de riego y una red de calles o autopistas. A menudo, hay puntos en el sistema en los que un flujo neto entra o sale del sistema. El principio básico detrás del análisis de tales sistemas es que el flujo total hacia el sistema debe ser igual al flujo total hacia afuera. De hecho, aplicamos este principio en todas las uniones del sistema.
Regla de cruce
En cada una de las uniones de la red, el flujo total hacia esa unión debe ser igual al flujo total hacia afuera. ◊
Este requisito da una ecuación lineal que relaciona los flujos en los conductores que emanan de la unión.
Ejemplo ilustrativo 1.4_1
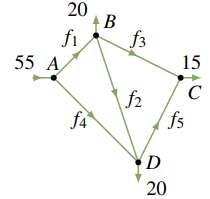
En el diagrama adjunto se muestra una red de calles de un solo sentido. La tasa de flujo de automóviles hacia la intersección A es de 500 automóviles por hora, y de B y C salen 400 y 100 automóviles por hora, respectivamente. Encuentra los posibles flujos a lo largo de cada calle.

Solución:
Suponga que los flujos a lo largo de las calles son f1, f2, f3, f4, f5 y f6 automóviles por hora en las direcciones que se muestran.
Luego, equiparando el flujo hacia adentro con el flujo hacia afuera en cada intersección, obtenemos
Intersección A 500 = f1 + f2 + f3
Intersección B f1 + f4 + f6= 400
Intersección C f3 + f5 = f6 +100
Intersección D f2 = f4 + f5
De lo anterior se deducen las siguientes ecuaciones lineales en las seis variables f1, f2, …, f6.

La reducción de la matriz aumentada es
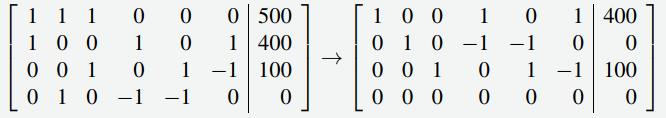
Por lo tanto, cuando usamos f4 f5 y f6 como parámetros, la solución general es
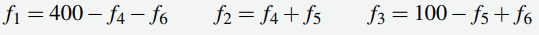
Esto da todas las soluciones al sistema de ecuaciones y, por tanto, todos los flujos posibles.
Por supuesto, no todas estas soluciones pueden ser aceptables en la situación real. Por ejemplo, los flujos f1, f2, …, f6 son todos positivos en el contexto actual (si uno sale negativo, significaría que el tráfico fluye en la dirección opuesta). Esto impone restricciones a los flujos: f1 ≥ 0 y f3 ≥ 0 se convierten en

Se podrían imponer más restricciones insistiendo en valores máximos en el flujo en cada calle.
Ejercicios propuestos para el Capítulo 1.4
1. Encuentre los posibles flujos en cada una de las siguientes redes de tuberías.

2. En el diagrama adjunto se describe una red propuesta de canales de riego. En el pico de demanda, los flujos en los intercambios A, B, C y D son los que se muestran
a. Encuentra los posibles flujos.
b. Si el canal BC está cerrado, ¿qué rango de flujo en AD debe mantenerse para que ningún canal lleve un flujo de más de 30?
3. Una rotonda tiene cinco calles de un solo sentido y los vehículos entran y salen como se muestra en el diagrama adjunto.

a. Calcule los posibles flujos.
b. ¿Qué camino tiene el flujo más pesado?
