Integrando expresiones que involucran √(x² − a²)
El dominio de la expresión √(x² − a²) es (−∞, −a] ∪ [a, + ∞). Por lo tanto, x ≤ − a o x ≥ a. Por lo tanto, x/a ≤ − 1 o x/a ≥ 1. Dado que estos intervalos corresponden al rango de secθ en el conjunto [0, π/2) ∪ (π/2, π], tiene sentido usar la sustitución secθ = x/a o, de manera equivalente, x = asecθ, donde 0 ≤ θ < π/2 o π/2 < θ ≤ π. La sustitución correspondiente para dx es dx = asecθtanθdθ. El procedimiento para utilizar esta sustitución se describe en la siguiente estrategia de resolución de problemas.
ESTRATEGIA DE RESOLUCIÓN DE PROBLEMAS 5.10_3: INTEGRALES QUE INVOLUCRAN √(x² − a²)
|
1. Verifique si la integral no puede evaluarse utilizando otro método. Si es así, podríamos considerar aplicar una técnica alternativa. 2. Sustituya x = asecθ y dx = asecθtanθdθ. Esta sustitución produce
Para x ≥ a, |atanθ| = atanθ y para x ≤ − a, |atanθ| = −atanθ. 3. Simplifica la expresión. |
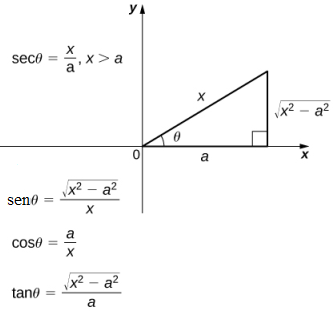


Figura 5.10_6 Use el triángulo de referencia apropiado para expresar las funciones trigonométricas evaluadas en θ en términos de x.
EJEMPLO ILUSTRATIVO 5.10_7. Encontrar el área de una región
Encuentre el área de la región entre la gráfica de f (x) = √(x² − 9) y el eje x sobre el intervalo [3, 5].
Solución:
Primero, dibuje un gráfico aproximado de la región descrita en el problema, como se muestra en la siguiente figura.


Podemos ver que el área está dada por


Para evaluar esta integral definida, sustituya x = 3secθ y dx = 3secθtanθdθ. También debemos cambiar los límites de la integración. Si x = 3, entonces 3 = 3secθ y por lo tanto θ = 0. Si x = 5, entonces θ = sec⁻¹(5/3). Después de hacer estas sustituciones y simplificar, tenemos
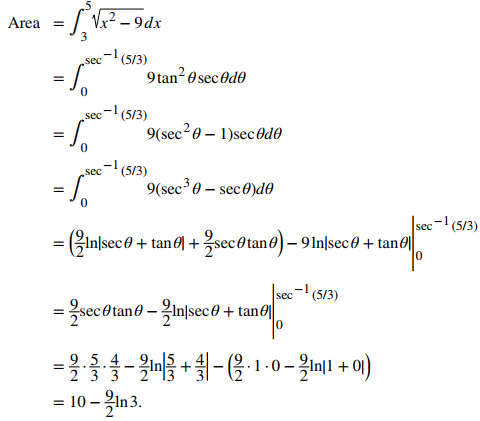
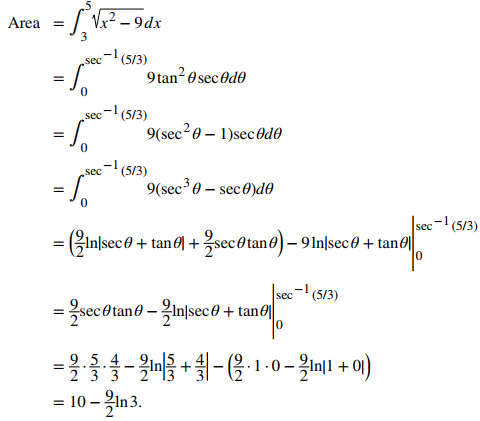
◊

