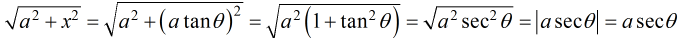Sustitución trigonométrica

Integrando expresiones que involucran √(a² + x²)

Para las integrales que contienen √(a² + x²), consideremos primero el dominio de esta expresión. Como √(a² + x²) se define para todos los valores reales de x, restringimos nuestra elección a aquellas funciones trigonométricas que tienen un rango de todos los números reales. Por lo tanto, nuestra elección se limita a seleccionar x = atanθ o x = acotθ. Cualquiera de estas sustituciones realmente funciona, pero la sustitución estándar es x = atanθ o, de manera equivalente, tanθ = x/a. Con esta sustitución, suponemos que -π/2) < θ < π/2, de modo que también tenemos θ = tan⁻¹(x/a). El procedimiento para usar esta sustitución se describe en la siguiente estrategia de resolución de problemas.

ESTRATEGIA PARA RESOLVER PROBLEMAS 5.10_2: INTEGRAR EXPRESIONES QUE INCLUYEN √(a² + x²)

Verifique si la integral se puede evaluar fácilmente utilizando otro método. En algunos casos, es más conveniente usar un método alternativo. Sustituya x = atanθ y dx = asec²θdθ. Esta sustitución produce (Dado que −π/2 < θ < π/2 y secθ > 0 durante este intervalo, |asecθ| = asecθ.) Simplifica la expresión. Evalúe la integral utilizando técnicas de la sección sobre integrales trigonométricas. Use el triángulo de referencia de la Figura 5.10_4 para reescribir el resultado en términos de x. También es posible que necesite usar algunas identidades trigonométricas y la relación θ = tan⁻¹(x/a). (Nota: el triángulo de referencia se basa en el supuesto de que x > 0; sin embargo, las relaciones trigonométricas producidas a partir del triángulo de referencia son las mismas que las relaciones para las cuales x ≤ 0.)

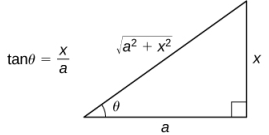
Figura 5.10_4 Se puede construir un triángulo de referencia para expresar las funciones trigonométricas evaluadas en θ en términos de x.

EJEMPLO ILUSTRATIVO 5.10_4. Integrando una expresión que involucra √(a² + x²)

Evaluary verifique la solución diferenciando.

Solución:
Comience con la sustitución x = tanθ y dx = sec²θdθ. Como tanθ = x, dibuja el triángulo de referencia en la siguiente figura.

De tal modo que

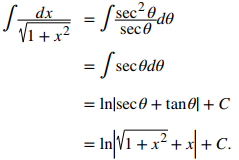
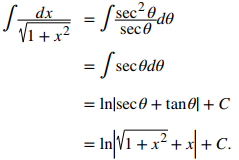
Para verificar la solución, diferencie:

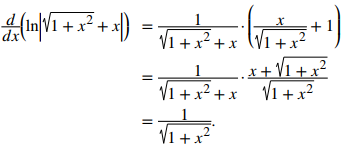
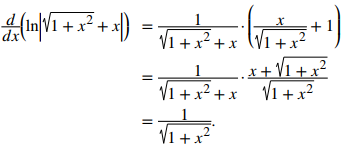
Como √(1 + x²) + x > 0 para todos los valores de x, podríamos reescribir ln∣√(1 + x²) + x∣ + C = ln (√(1 + x²) + x) + C, si lo desea. ◊

EJEMPLO ILUSTRATIVO 5.10_5. Integrando una expresión que involucra √(a² + x²)

EvaluarUsando una sustitución diferente a la del ejemplo anterior.

Solución:

Use la sustitución x = senhθ.

Debido a que senhθ tiene un rango de todos los números reales, y 1 + senh²θ = cosh²θ, también podemos usar la sustitución x = senhθ para evaluar esta integral. En este caso, dx = coshθdθ. Por consiguiente,

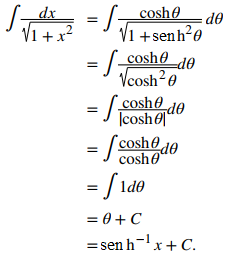
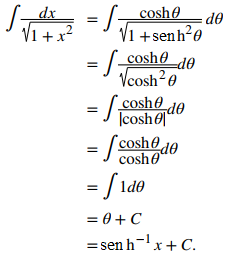
Análisis

Esta respuesta se ve bastante diferente de la respuesta obtenida usando la sustitución x = tanθ. Para ver que las soluciones son las mismas, establezca y = senh⁻¹x. Por lo tanto, senhy = x. De esta ecuación obtenemos:

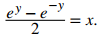
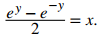
Después de multiplicar ambos lados por 2eʸ y reescribir, esta ecuación se convierte en:

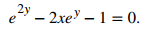
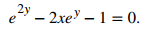
Usa la ecuación cuadrática para resolver por eʸ:

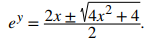
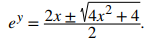
Simplificando, tenemos:

Como x − √(x² + 1) < 0, debe ser el caso de que eʸ = x + √(x² + 1). Así,

Por último, obtenemos

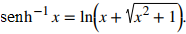
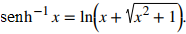
Después de hacer la observación final que x + √(x² + 1) > 0,

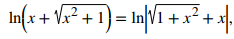
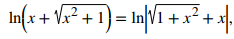
vemos que los dos métodos diferentes produjeron soluciones equivalentes. ◊

EJEMPLO ILUSTRATIVO 5.10_6. Encontrar una longitud de arco

Encuentre la longitud de la curva y = x² sobre el intervalo [0, 1/2].

Solución:
Como dy/dx = 2x, la longitud del arco viene dada por

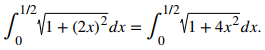
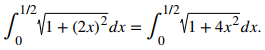
Para evaluar esta integral, use la sustitución x = (1/2)tanθ y dx = (1/2)sec²θdθ. También necesitamos cambiar los límites de la integración. Si x = 0, entonces θ = 0 y si x = 1/2, entonces θ = π/4. Así,

◊