| 7. Sucesiones y series infinitas | 7.2 Series infinitas |
La serie armónica
Una serie útil que se debe conocer es la serie armónica. La serie armónica se define como


Esta serie es interesante porque diverge, pero diverge muy lentamente. Con esto queremos decir que los términos en la sucesión de sumas parciales {Sk} se aproximan al infinito, pero lo hacen muy lentamente. Mostraremos que la serie diverge, pero primero ilustramos el lento crecimiento de los términos en la sucesión {Sk} en la siguiente tabla.
| k | 10 | 100 | 1000 | 10,000 | 100,000 | 1,000,000 |
| Sk | 2.92897 | 5.18738 | 7.48547 | 9.78761 | 12.09015 | 14.39273 |
Incluso después de 1,000,000 de términos, la suma parcial sigue siendo relativamente pequeña. De esta tabla, no está claro que esta serie realmente diverja. Sin embargo, podemos mostrar analíticamente que la sucesión de sumas parciales diverge y, por lo tanto, que la serie diverge.
Para mostrar que la sucesión de sumas parciales diverge, mostramos que la sucesión de sumas parciales no tiene límite. Comenzamos escribiendo las primeras sumas parciales:
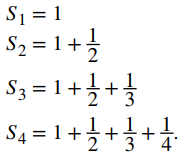
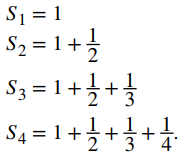
Observe que para los últimos dos términos en S4,


Por lo tanto, concluimos que
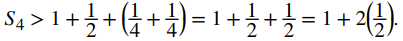
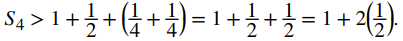
Usando la misma idea para S8, vemos que
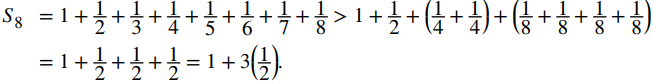
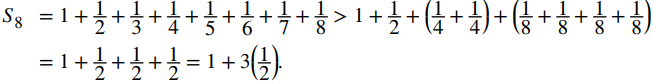
A partir de este patrón, vemos que S1 = 1, S2 = 1 + 1/2, S4 > 1 + 2 (1/2) y S8 > 1 + 3 (1/2).
De manera más general, se puede demostrar que S2 j > 1 + j(1/2) para todo j > 1. Como 1 + j(1/2) → ∞, concluimos que la sucesión {Sk} no está acotada y, por lo tanto, diverge. En la sección anterior, declaramos que las sucesiones convergentes están acotadas. En consecuencia, dado que {Sk} es no acotada, diverge. Por lo tanto, la serie armónica diverge.
Propiedades algebraicas de las series convergentes
Dado que la suma de una serie infinita convergente se define como un límite de una sucesión, las propiedades algebraicas para las series que se enumeran a continuación se derivan directamente de las propiedades algebraicas para las sucesiones.
Teorema 7.2.1. Propiedades algebraicas de las series convergentes


EJEMPLO ILUSTRATIVO 7.2_2. Uso de propiedades algebraicas de series convergentes
Evaluar


Solución:
Mostramos antes que


y que
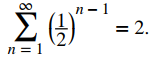
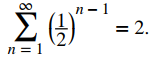
Dado que ambas series convergen, podemos aplicar las propiedades algebraicas de las series convergentes para evaluar
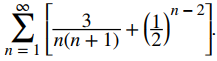
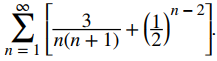
Usando la regla de la suma, se escribe


Luego, usando la regla del múltiplo constante y las sumas anteriores, podemos concluir que


Series geométricas
Una serie geométrica es cualquier serie que podamos escribir en la forma
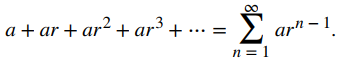
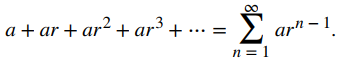
Debido a que la razón de cada término en esta serie al término anterior es r, el número r se llama razón de la serie geométrica. Nos referimos a a como el término inicial porque es el primer término de la serie. Por ejemplo, la serie
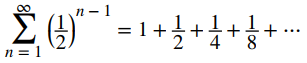
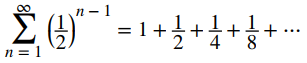
es una serie geométrica con término inicial a = 1 y razón r = 1/2.
En general, ¿cuándo converge una serie geométrica? Considere la serie geométrica
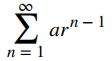
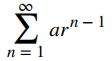
cuando a > 0. La sucesión de sumas parciales {Sk} viene dada por
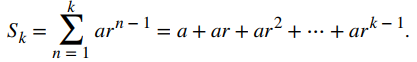
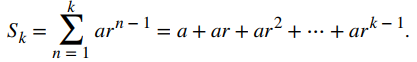
Considere el caso cuando r = 1. En ese caso,


Como a > 0, vemos ak → ∞ cuando k → ∞. Por lo tanto, la sucesión de sumas parciales no está acotada y, por lo tanto, diverge. En consecuencia, la serie infinita diverge para r = 1. Cuando r ≠ 1, para encontrar el límite de {Sk}, se multiplica la la serie geométrica por 1 − r. Al hacer esto último, vemos que
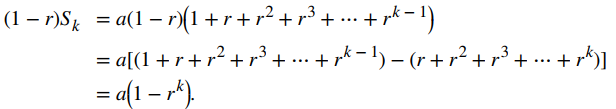
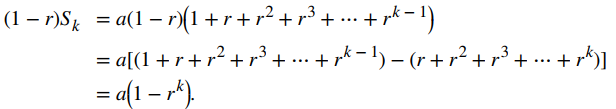
Todos los demás términos se cancelan.
Por lo tanto,
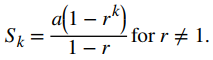
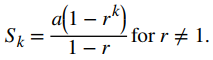
De nuestra discusión en la sección anterior, sabemos que la secuencia geométrica r k → 0 si |r | < 1 y que r k diverge si |r | > 1 o r = ± 1. Por lo tanto, para |r | < 1, Sk → a / (1 − r) y tenemos


Si |r | ≥ 1, Sk diverge, y por lo tanto
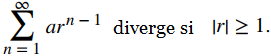
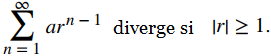
Definición 7.2.2. Serie geométrica
Una serie geométrica es una serie de la forma.
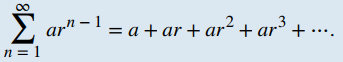
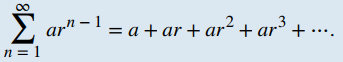
Si |r | < 1, la serie converge y


Si |r | ≥ 1, la serie diverge. ♦
Las series geométricas a veces aparecen en formas ligeramente diferentes. Por ejemplo, a veces el índice comienza en un valor distinto de n = 1 o el exponente implica una expresión lineal para n que no sea n − 1. Mientras podamos reescribir la serie en la forma


estamos tratando con una serie geométrica.
Por ejemplo, considere la serie


Para ver que esta es una serie geométrica, escribimos los primeros términos:
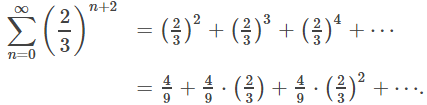
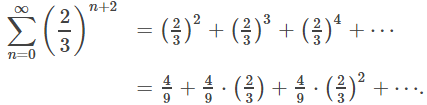
Vemos que el término inicial es a = 4/9 y la razón es r = 2/3. Por lo tanto, la serie se puede escribir como
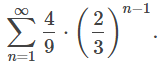
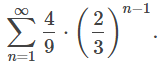
Como r = 2/3 < 1, esta serie converge, y su suma viene dada por
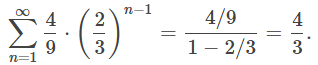
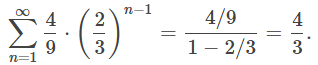
EJEMPLO ILUSTRATIVO 7.2_3. Determinación de la convergencia o divergencia de una serie geométrica
Determine si cada una de las siguientes series geométricas converge o diverge, y si converge, encuentre su suma.
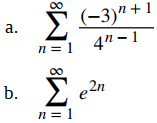
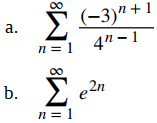
Solución:
a. Escribiendo los primeros términos de la serie, tenemos
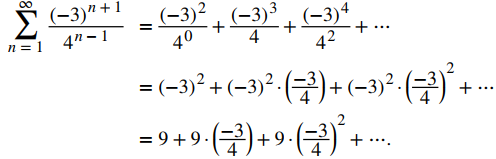
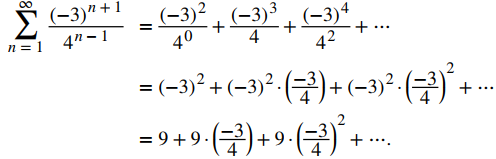
El término inicial a = −3 y la razón r = −3/4. Como |r| = 3/4 < 1, la serie converge a


b. Escribiendo esta serie como


Podemos ver que esta es una serie geométrica donde r = e² > 1. Por lo tanto, la serie diverge.
Ahora dirigimos nuestra atención a una buena aplicación de series geométricas. Mostramos cómo se pueden usar para escribir decimales periódicos como fracciones de enteros.
EJEMPLO ILUSTRATIVO 7.2_4. Escribir decimales periódicos como fracciones de enteros
Usa una serie geométrica para escribir


como una fracción de enteros.
Solución:
Ya que


primero escribimos


Ignorando el primer término, 3, el resto de esta expresión es una serie geométrica con un término inicial a = 26/10² y una razón r = 1/10². Por lo tanto, la suma de esta serie es


Así,
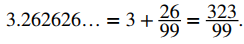
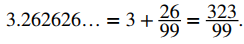
EJEMPLO ILUSTRATIVO 7.2_5. Encontrar el área del copo de nieve de Koch
Defina una secuencia de figuras {Fn} de forma recursiva de la siguiente manera (Figura 7.2_2). Sea F0 un triángulo equilátero con lados de longitud 1. Para n ≥ 1, sea Fn la curva creada al eliminar el tercio medio de cada lado de Fn − 1 y reemplazarlo con un triángulo equilátero que apunta hacia afuera. La cifra limitante como n → ∞ se conoce como copo de nieve de Koch.

a. Encuentre la longitud Ln del perímetro de Fn. Evalúe limn → ∞ Ln para encontrar la longitud del perímetro del copo de nieve de Koch.
b. Encuentre el área An de la figura Fn. Evalúe limn → ∞ An para encontrar el área del copo de nieve de Koch.
Solución:
Deje Nn denotar el número de lados de la figura Fn. Como F0 es un triángulo, N0 = 3. Deje que ln denote la longitud de cada lado de Fn. Como F0 es un triángulo equilátero con lados de longitud l0 = 1, ahora necesitamos determinar N1 y l1. Dado que F1 se crea eliminando el tercio medio de cada lado y reemplazando ese segmento de línea con dos segmentos de línea, para cada lado de F0, obtenemos cuatro lados en F1. Por lo tanto, el número de lados para F1 es
N1 = 4⋅3.
Como la longitud de cada uno de estos nuevos segmentos de línea es 1/3 de la longitud de los segmentos de línea en F0 , la longitud de los segmentos de línea para F0 viene dada por
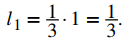
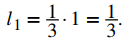
Del mismo modo, para F2, dado que el tercio medio de cada lado de F1 se elimina y se reemplaza con dos segmentos de línea, el número de lados en F2 viene dado por


Como la longitud de cada uno de estos lados es 1/3 de la longitud de los lados de F1, la longitud de cada lado de la figura F2 viene dada por
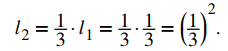
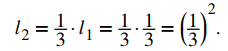
De manera más general, dado que Fn se crea al eliminar 1/3 de cada lado de Fn − 1 y reemplazar ese segmento de línea con dos segmentos de línea de longitud (1/3) ln − 1 en forma de triángulo equilátero, sabemos que
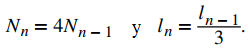
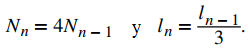
Por lo tanto, el número de lados de la figura Fn es


y la longitud de cada lado es


Por lo tanto, para calcular el perímetro de Fn, multiplicamos el número de lados Nn y la longitud de cada lado ln. Concluimos que el perímetro de Fn viene dado por
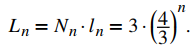
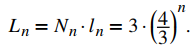
Por lo tanto, la longitud del perímetro del copo de nieve de Koch es
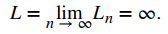
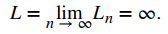
b. Deje que Tn denote el área de cada nuevo triángulo creado al formar Fn. Para n = 0, T0 es el área del triángulo equilátero original. Por lo tanto, T0 = A0 = √3 / 4. Para n ≥ 1, dado que las longitudes de los lados del nuevo triángulo son 1/3 de la longitud de los lados de Fn − 1, tenemos


Por lo tanto, Tn = (1/9)ⁿ⋅√3/4. Como se forma un nuevo triángulo en cada lado de Fn − 1,
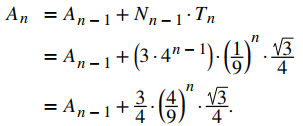
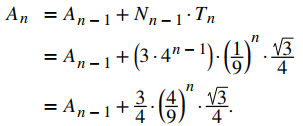
Al escribir los primeros términos A0, A1, A3, vemos que


Más generalmente,


Factorizando 4/9 de cada término dentro de los paréntesis internos, reescribimos nuestra expresión como
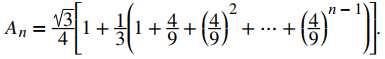
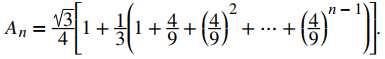
La expresión


Es una suma geométrica. Como se mostró anteriormente, esta suma satisface
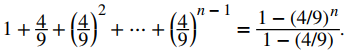
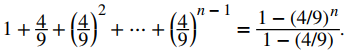
Sustituyendo esta expresión en la expresión anterior y simplificando, concluimos que


Por lo tanto, el área del copo de nieve de Koch es


|
Análisis
converge, el área de esta región es finita, aunque el perímetro es infinito. |
Serie telescópica
Considere la serie
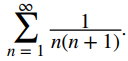
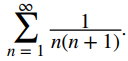
Al usar fracciones parciales, podemos escribir
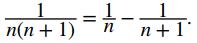
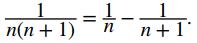
Por lo tanto, la serie se puede escribir como
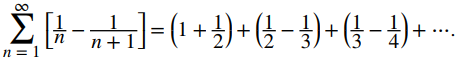
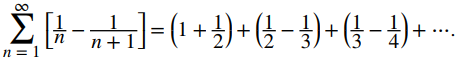
Al escribir los primeros términos en la sucesión de sumas parciales {Sk}, vemos que
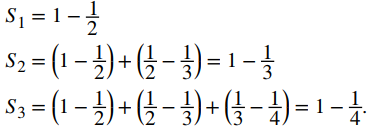
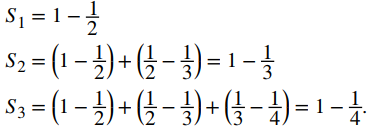
en general
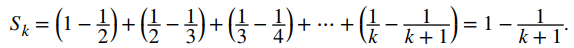
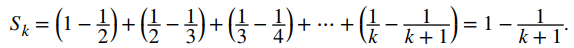
Notamos que los términos intermedios se cancelan mutuamente, dejando solo el primero y el último término. En cierto sentido, la serie se derrumba como un catalejo con tubos que desaparecen entre sí para acortar el telescopio. Por esta razón, llamamos a una serie que tiene esta propiedad una serie telescópica. Para esta serie, dado que Sk = 1 − 1/(k + 1) y 1/(k + 1) → 0 cuando k → ∞, la sucesión de sumas parciales converge a 1 y, por lo tanto, la serie converge a 1.
Definición 7.2.3. Serie telescópica
Una serie telescópica es una serie en la que la mayoría de los términos se cancelan en cada una de las sumas parciales, dejando solo algunos de los primeros términos y algunos de los últimos.
Por ejemplo, cualquier serie de la forma
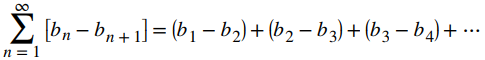
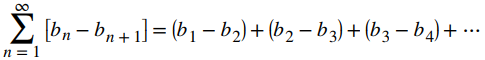
es una serie telescópica Podemos ver esto escribiendo algunas de las sumas parciales. En particular, vemos que


En general, la suma parcial enésima de esta serie es


Dado que la suma parcial enésima se puede simplificar a la diferencia de estos dos términos, la sucesión de sumas parciales {Sk} convergerá si y solo si la secuencia {bk + 1} converge. Además, si la sucesión bk + 1 converge a algún número finito B, entonces la sucesión de sumas parciales converge a b1 − B, y por lo tanto


En el siguiente ejemplo, mostramos cómo usar estas ideas para analizar una serie telescópica de esta forma.
EJEMPLO ILUSTRATIVO 7.2_6. Evaluación de una serie telescópica
Determinar si la serie telescópica
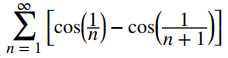
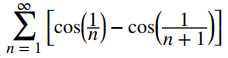
converge o diverge Si converge, encuentre su suma.
Solución:
Al escribir términos en la secuencia de sumas parciales, podemos ver que


En general,
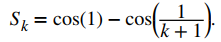
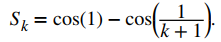
Dado que 1 / (k + 1) → 0 cuando k → ∞ y cosx es una función continua, cos (1 / (k + 1)) → cos (0) = 1. Por lo tanto, concluimos que Sk → cos (1) −1. La serie telescópica converge y la suma viene dada por
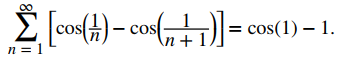
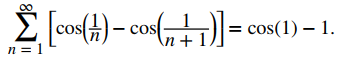


PEDRO PABLO MONTOYA: ACÁ ESTÁ MI COMENTARIO.