| 3.3 Reglas de diferenciación |

Ejercicios propuestos para el Capítulo 3.3

        Para los siguientes ejercicios, encuentra f ′(x) para cada función:

106. \(f(x) = x^7 + 10\)
107. \(f(x) = 5x^3 – x + 1\)
108. \(f(x) = 4x^2 – 7x\)
109. \(f(x) = 8x^4 + 9x^2 – 1\)
110. \(f(x) = x^4 + \frac{2}{x}\)
111. \(f(x) = 3x\left(18x^4 + \frac{13}{x+1}\right)\)
112. \(f(x) = (x+2)(2x^2 – 3)\)
113. \(f(x) = x^2\left(\frac{2}{x^2} + \frac{5}{x^3}\right)\)
114. \(f(x) = \frac{x^3 + 2x^2 – 4}{3}\)
115. \(f(x) = \frac{4x^3 – 2x + 1}{x^2}\)
116. \(f(x) = \frac{x^2 + 4}{x^2 – 4}\)
117. \(f(x) = \frac{x + 9}{x^2 – 7x + 1}\)

      Para los siguientes ejercicios, encuentra la ecuación de la línea tangente T(x) a la gráfica de la función dada en el punto indicado. Usa una calculadora gráfica para graficar la función y la línea tangente:

118. [T] \(y = 3x^2 + 4x + 1\) en \((0,1)\)
119. [T] \(y = \frac{2}{x^2} + 1\) en \((1,3)\)
120. [T] \(y = \frac{2x}{x-1}\) en \((-1, 1)\)
121. [T] \(y = \frac{2}{x} – \frac{3}{x^2}\) en \((1, -1)\)

      Para los siguientes ejercicios, asume que f (x) y g(x)son funciones diferenciables para todo xx. Encuentra la derivada de cada una de las funciones h(x):

122. \(h(x) = 4f(x) + \frac{g(x)}{7}\)
123. \(h(x) = x^3 f(x)\)
124. \(h(x) = \frac{f(x)g(x)}{2}\)
125. \(h(x) = \frac{3f(x)}{g(x) + 2}\)

      Para los siguientes ejercicios, asume que f (x) y g(x) son funciones diferenciables con valores dados en la siguiente tabla. Usa la siguiente tabla para calcular las siguientes derivadas:

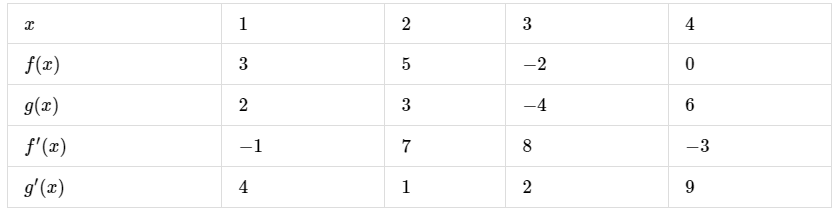
126. Encuentra \(h'(1)\) si \(h(x) = xf(x) + 4g(x)\).
127. Encuentra \(h'(2)\) si \(h(x) = \frac{f(x)}{g(x)}\).
128. Encuentra \(h'(3)\) si \(h(x) = 2x + f(x)g(x)\).
129. Encuentra \(h'(4)\) si \(h(x) = \frac{1}{x} + \frac{g(x)}{f(x)}\).

        Para los siguientes ejercicios, usa la siguiente figura para encontrar las derivadas indicadas, si existen:

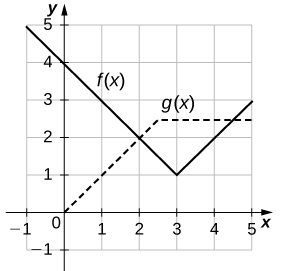
130. Sea \(h(x) = f(x) + g(x)\). Encuentra
a. \(h'(1)\),
b. \(h'(3)\), y
c. \(h'(4)\).

131. Sea \(h(x) = f(x)g(x)\). Encuentra
a. \(h'(1)\),
b. \(h'(3)\), y
c. \(h'(4)\).

132. Sea \(h(x) = \frac{f(x)}{g(x)}\). Encuentra
a. \(h'(1)\),
b. \(h'(3)\), y
c. \(h'(4)\).

Para los siguientes ejercicios,

a. evalúa \(f'(a)\), y
b. grafica la función \(f(x)\) y la recta tangente en \(x = a\).

133. [T] \(f(x) = 2x^3 + 3x – x^2\), \(a = 2\)
134. [T] \(f(x) = \frac{1}{x} – x^2\), \(a = 1\)
135. [T] \(f(x) = x^2 – x^{12} + 3x + 2\), \(a = 0\)
136. [T] \(f(x) = \frac{1}{x} – x^2\), \(a = -1\)

137. Encuentra la ecuación de la recta tangente a la gráfica de \(f(x) = 2x^3 + 4x^2 – 5x – 3\) en \(x = -1\).

138. Encuentra la ecuación de la recta tangente a la gráfica de \(f(x) = x^2 + \frac{4}{x} – 10\) en \(x = 8\).

139. Encuentra la ecuación de la recta tangente a la gráfica de \(f(x) = (3x – x^2)(3 – x – x^2)\) en \(x = 1\).

140. Encuentra el punto en la gráfica de \(f(x) = x^3\) tal que la recta tangente en ese punto tiene una intersección en x de 6.

141. Encuentra la ecuación de la recta que pasa por el punto \(P(3, 3)\) y es tangente a la gráfica de \(f(x) = \frac{6}{x – 1}\).

142. Determina todos los puntos en la gráfica de \(f(x) = x^3 + x^2 – x – 1\) para los cuales
a. la recta tangente es horizontal
b. la recta tangente tiene una pendiente de −1.

143. Encuentra un polinomio cuadrático tal que \(f(1) = 5\), \(f'(1) = 3\) y \(f″(1) = -6\).

144. Un coche que circula por una autopista con tráfico ha recorrido
\[s(t) = t^3 – 6t^2 + 9t\] metros en t segundos.
a. Determina el tiempo en segundos cuando la velocidad del coche es 0.
b. Determina la aceleración del coche cuando la velocidad es 0.

145. [T] Un arenque nadando en línea recta ha recorrido \[s(t) = \frac{t^2}{t^2 + 2}\] pies en t segundos. Determina la velocidad del arenque cuando ha transcurrido 3 segundos.

146. La población en millones de platijas árticas en el Océano Atlántico está modelada por la función \[P(t) = \frac{8t + 3}{0.2t^2 + 1},\] donde t se mide en años.
a. Determina la población inicial de platijas.
b. Determina \(P'(10)\) e interpreta brevemente el resultado.

147. [T] La concentración de antibiótico en el torrente sanguíneo t horas después de ser inyectado está dada por la función \[C(t) = \frac{2t^2 + t}{t^3 + 50},\] donde C se mide en miligramos por litro de sangre.
a. Encuentra la tasa de cambio de \(C(t)\).
b. Determina la tasa de cambio para \(t = 8, 12, 24,\) y \(36\).
c. Describe brevemente lo que parece estar ocurriendo a medida que aumenta el número de horas.

148. Una editorial de libros tiene una función de costo dada por \[C(x) = \frac{x^3 + 2x + 3}{x^2},\] donde x es el número de copias de un libro en miles y C es el costo, por libro, medido en dólares. Evalúa \(C'(2)\) y explica su significado.

149. [T] De acuerdo con la ley de gravitación universal de Newton, la fuerza F entre dos cuerpos de masa constante m₁ y m₂ está dada por la fórmula \[F = \frac{Gm_1 m_2}{d^2},\] donde G es la constante gravitacional y d es la distancia entre los cuerpos.
a. Supón que G, m₁ y m₂ son constantes. Encuentra la tasa de cambio de la fuerza F con respecto a la distancia d.
b. Encuentra la tasa de cambio de la fuerza F con la constante gravitacional \(G = 6.67 \times 10^{-11} \frac{Nm^2}{kg^2}\), sobre dos cuerpos separados por 10 metros, cada uno con una masa de 1000 kilogramos.