Razones
El concepto de razón surge cuando deseamos comparar dos cantidades. Básicamente las cantidades se pueden comparar de dos maneras distintas: Por diferencia o por cociente.
La primera cantidad que se nombra en la comparación se denomina antecedente y la segunda consecuente. La palabra genérica para antecedente y consecuente es término.
Razón por diferencia o razón aritmética
La razón aritmética de dos cantidades dadas es la diferencia indicada de las cantidades.
♦ En esta comparación lo que se desea saber es en cuántas unidades excede una cantidad (el antecedente) a la otra cantidad (el consecuente).
Razón por cociente o razón geométrica
La razón geométrica de dos cantidades dadas es el cociente indicado de las cantidades.
♦ En esta comparación lo que se desea saber es cuántas veces una cantidad contiene a la otra.
♦ Las razones geométricas se pueden denotar de dos maneras diferentes, en forma de fracción simple o mediante dos puntos (:). Por ejemplo la razón geométrica de 7 y 12 que se lee “7 es a 12” se puede escribir como:

En este ejemplo, los términos de la razón son respectivamente, 7 el antecedente y 12 el consecuente.
♦ Toda razón geométrica se puede simplificar a una fracción irreductible (los términos son primos entre sí), a esta simplificación se le llama resultado o valor de la razón. Por ejemplo, el resultado de la razón 21:6 es su forma simplificada 7:2 (al dividir cada término entre 3 se obtiene una fracción irreductible).
Ejemplo ilustrativo 1
La edad de un padre es de 54 años y la de su hijo mayor de 36 años. Hallar la razón geométrica entre las edades del padre y el hijo.
Solución:
Establecemos el cociente indicado entre las edades del padre (antecedente) y la de su hijo (consecuente):

Simplificamos la fracción dividiendo tanto el numerador como el denominador por el MCM [36, 54] = 18 (mínimo común múltiplo de 36 y 54):

Respuesta: La edad del padre es a la de su hijo como 3 es a 2: Por cada 3 años que ha cumplido el padre su hijo mayor ha cumplido 2 (tenga presente que la unidad de medida es el año). ◊
Proporciones
Una proporción es la igualdad indicada de dos razones. Por supuesto hay dos tipos distintos de proporciones, la aritmética y la geométrica.
Proporción aritmética
Una proporción aritmética o equidiferencia es la igualdad entre dos razones aritméticas.
Proporción geométrica
Una proporción geométrica o equicociente es la igualdad entre dos razones geométricas.
♦Se acostumbra nombrar a una proporción geométrica simplemente como “proporción”, como haremos de aquí en adelante.
♦ Cada uno de los cuatro términos de una proporción se denomina cuarta proporcional.
♦ El numerador de la primera razón (fracción) y el denominador de la segunda son los extremos de la proporción y el denominador de la primera razón y el numerador de la segunda son los medios de la proporción. Por ejemplo, en la proporción

a y d son los extremos y b y c los medios.
Propiedades de las proporciones
Propiedad fundamental
En una proporción el producto de los extremos es igual al producto de los medios .
Esto es,
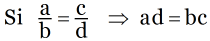
Otras propiedades fundamentales de las proporciones


Media proporcional
Se llama media proporcional a cada uno de los medios de una proporción cuyos medios son iguales.
Propiedad de la media proporcional
La media proporcional es igual a la raíz cuadrada del producto de los extremos.
Esto es,

Cuarta proporcional
La cuarta proporcional es uno cualquiera de los cuatro términos de una proporción con respecto a los otros tres.
Supongamos que conocemos los valores numéricos de tres de los cuatro términos de una proporción y desconocemos el cuarto. Este cuarto término se puede calcular como sigue
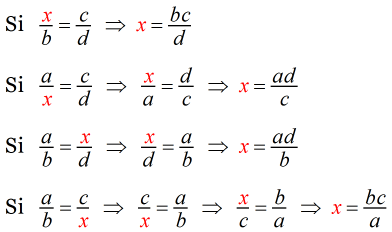
Tercera proporcional
En una proporción donde los medios son iguales, la tercera proporcional es cualquiera de los extremos.
Esto es, en la proporción

a es una tercera proporcional de b y c, y c es una tercera proporcional dea y b.
