Comportamiento final de una función

El comportamiento de una función cuando x → ± ∞ se denomina comportamiento final de la función. En cada uno de los extremos de la función, la función podría exhibir uno de los siguientes tipos de comportamiento:

1.  La función f(x) se aproxima a una asíntota horizontal y = L.

2.  La función f(x) → ∞  o  f(x) → −∞.

3.  La función no se acerca a un límite finito, ni se acerca a ∞ o −∞. En este caso, la función puede tener algún comportamiento oscilatorio.

Consideremos aquí varias clases de funciones y veamos los diferentes tipos de comportamientos finales para estas funciones.

Comportamiento final para funciones polinomiales

Considere la función de potencia f(x) = xⁿ donde n es un número entero positivo. De la Figura 4.27 y la Figura 4.28, vemos que

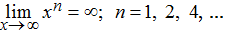
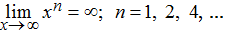
y

Teniendo en cuenta estos hechos, no es difícil evaluar

donde c es cualquier constante y n es un número entero positivo. Si c > 0, la gráfica de y = cxⁿ es un estiramiento vertical o compresión de y = xⁿ, y por lo tanto

Si c < 0, la gráfica de y = cxⁿ es un estiramiento vertical o compresión combinada con una reflexión sobre el eje x, y por lo tanto

Si c = 0, y = cxⁿ = 0, en cuyo caso

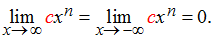
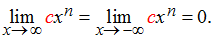
Ahora veamos cómo se pueden usar los límites en el infinito para las funciones potencia y determinar el

para cualquier función polinómica f.

Considere una función polinómica

de grado n ≥ 1 con a_n ≠ 0. Factorizando, vemos que

Cuando x → ± ∞, todos los términos dentro del paréntesis, excepto el primero, se acercan a cero. Concluimos que

Por ejemplo, la función f(x) = 5x³ − 3x² + 4 se comporta como g(x) = 5x³ cuando x → ± ∞ como se muestra en la Figura 4.29 y la Tabla 4.4.

x	1010	100	1000
f(x)=5x3−3x2+4	4704	4,970,0044	4,997,000,004
g(x)= 5x3	5000	5,000,000	5,000,000,
x	−10	−100	−1000
f(x)=5x3−3x2+4	−5296	−5,029,996	−5,002,999,996
g(x)= 5x3	−5000	−5,000,000	−5,000,000,000

Tabla 4.4  Un comportamiento final de un polinomio está determinado por el término con el mayor exponente.

Comportamiento final para funciones algebraicas

El comportamiento final para funciones racionales y funciones que involucran radicales es un poco más complicado que para polinomios. Los límites en el infinito de una función racional f(x) = p(x) / q(x) dependen de la relación entre el grado del numerador y el grado del denominador. Para evaluar los límites en el infinito para una función racional, dividimos el numerador y el denominador por la potencia más alta de x que aparece en el denominador. Esto determina qué término en la expresión general domina el comportamiento de la función en valores grandes de x.

Antes de continuar, consideremos la gráfica de f(x) = (3x² + 4x) / (x + 2) que se muestra en la Figura 4.30. Cuando x → ∞  y  x → −∞, la gráfica de f aparece casi lineal. Aunque f ciertamente no es una función lineal, ahora investiguemos por qué la gráfica de f parece acercarse a una función lineal. Primero, usando la división larga de polinomios, podemos escribir

Como 4 / (x + 2) → 0 cuando x → ± ∞, concluimos que

Por lo tanto, la gráfica de f se aproxima a la recta y = 3x − 2 cuando x → ± ∞. Esta recta se conoce como asíntota oblicua para f (figura 4.30).

Comportamiento final para funciones racionales.

Considere una función racional

donde a_n ≠ 0  y  b_m ≠ 0.

1.  Si el grado del numerador es el mismo que el del denominador (n = m), entonces f tiene una asíntota horizontal de y = a_n / b_m cuando x → ± ∞.

2.  Si el grado del numerador es menor que el grado del denominador (n < m), entonces f tiene una asíntota horizontal de y = 0 cuando x → ± ∞.

3.  Si el grado del numerador es mayor que el grado del denominador (n > m), entonces f no tiene una asíntota horizontal. Los límites en el infinito son infinito positivo o negativo, dependiendo de los signos de los términos principales. Además, usando la división larga, la función puede reescribirse como

donde el grado de r(x) es menor que el grado de q(x). Como resultado,

Por lo tanto, los valores de [ f(x) − g(x)] se aproximan a cero cuando x → ± ∞. Si el grado de p (x) es exactamente uno más que el grado de q(x) (n = m + 1), la función g(x) es una función lineal. En este caso, llamamos a g(x) una asíntota oblicua.

Determinación del comportamiento final para funciones trascendentales

Las seis funciones trigonométricas básicas son periódicas y no se acercan a un límite finito cuando x → ± ∞. Por ejemplo, senx oscila entre 1 y − 1 (Figura 4.31). La función tanx tiene un número infinito de asíntotas verticales cuando x → ± ∞; por lo tanto, no se acerca a un límite finito ni se acerca a ± ∞ como x → ± ∞ como se muestra en la Figura 4.32.

Recuerde que para cualquier base b > 0, b ≠ 1, la función y = b^x es una función exponencial con dominio (−∞, ∞) y rango (0, ∞). Si b > 1, y = b^x aumenta en (−∞, ∞). Si 0 < b < 1, y = = b^x disminuye en (−∞, ∞). Para la función exponencial natural f(x) = e^x, e ≈ 2.718 > 1. Por lo tanto, f(x) = e^x está aumentando en (−∞, ∞) y el rango es (0, ∞). La función exponencial f(x) = e^x se aproxima a ∞ cuando x → ∞ y se aproxima a 0 cuando x → −∞ como se muestra en la Tabla 4.5 y la Figura 4.33.

x	−5	−2	0	2	5
ex	0.00674	0.135	1	7.389	148.413

Tabla 4.5  Comportamiento final de la función exponencial natural

Recuerde que la función de logaritmo natural f(x) = ln(x) es la inversa de la función exponencial natural y = e^x. Por lo tanto, el dominio de f(x) = ln(x) es (0, ∞) y el rango es (−∞, ∞). La gráfica de f(x) = ln(x) es el reflejo de la gráfica de y = e^x  sobre la recta y = x. Por lo tanto, ln(x) → −∞ cuando x → 0⁺ y ln(x) → ∞ cuando x → ∞ como se muestra en la Figura 4.34 y la Tabla 4.6.

x	0.01	0.1	1	10	100
ln(x)	−4.605	−2.303	0	2.303	4.605

Tabla 4.6  Comportamiento final de la función logaritmo natural

Pautas para dibujar la gráfica de una función

Ahora tenemos suficientes herramientas analíticas para dibujar las gráficas de una amplia variedad de funciones algebraicas y trascendentales. Antes de mostrar cómo graficar funciones específicas, veamos una estrategia general para usar al graficar cualquier función.

Dada una función f, siga los siguientes pasos para dibujar su gráfica:

1.  Determine el dominio de la función.

2.  Localice las intercepciones en los ejes x  e  y.

3.  Evalúe el limx → ∞ de f(x) y el limx → −∞ de f(x) para determinar el comportamiento final. Si cualquiera de estos límites es un número finito L, entonces y = L es una asíntota horizontal. Si alguno de estos límites es ∞ o −∞, determine si f tiene una asíntota oblicua. Si f es una función racional tal que f(x) = p(x) / q(x), donde el grado del numerador es mayor que el grado del denominador, entonces f puede escribirse como f(x) = p(x) / q(x) = g(x) + r(x) / q(x), donde el grado de r(x) es menor que el grado de q(x). Los valores de f(x) se aproximan a los valores de g(x) cuando x → ± ∞. Si g(x) es una función lineal, se conoce como asíntota oblicua.

4.  Determine si f tiene alguna asíntota vertical.

5.  Calcule f ′. Encuentre todos los puntos críticos y determine los intervalos donde f crece y donde f decrece. Determine si f tiene algún extremo local.

6.  Calcule f ”. Determine los intervalos donde f es cóncava hacia arriba y donde f es cóncava hacia abajo. Use esta información para determinar si f tiene algún punto de inflexión. La segunda derivada también se puede usar como un medio alternativo para determinar o verificar que f tiene un extremo local en un punto crítico.

Ejercicios resueltos