Límites infinitos en el infinito
Algunas veces los valores de una función f se vuelven arbitrariamente grandes cuando x → ∞ (o cuando x → −∞). En este caso, escribimos
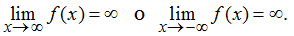
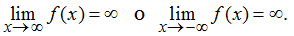
Por otro lado, si los valores de f son negativos pero se vuelven arbitrariamente grandes en magnitud cuando x → ∞ (o cuando x → −∞), escribimos


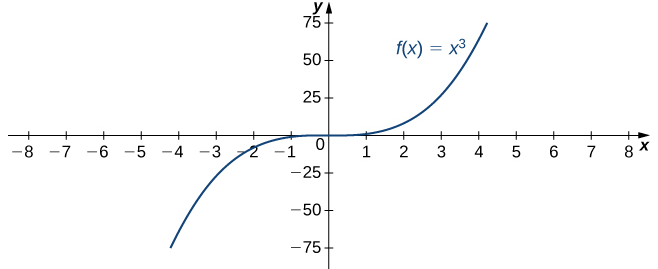
Por ejemplo, considere la función f(x) = x3. Como se ve en la Tabla 4.3 y la Figura 4.24, cuando x → ∞ los valores de f(x) se vuelven arbitrariamente grandes. Por lo tanto,


Por otro lado, cuando x → −∞, los valores de f(x) = x3 son negativos pero se vuelven arbitrariamente grandes en magnitud. En consecuencia,


| x | 10 | 20 | 50 | 100 | 1000 |
| x3 | 1000 | 8000 | 125,000 | 1,000,000 | 1,000,000,000 |
| x | −10 | −20 | −50 | −100 | −1000 |
| x3 | −1000 | −8000 | −125,000 | −1,000,000 | −1,000,000,000 |
Tabla 4.3 Valores de la función “tercera potencia” cuando x → ± ∞

Definición 4.6.3 (Informal). Límite infinito en el infinito
Decimos que una función f tiene un límite infinito en el infinito y escribimos


si f(x) se vuelve arbitrariamente grande para x suficientemente grande.
Decimos que una función tiene un límite infinito negativo en el infinito y escribimos
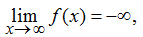
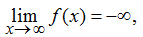
Definiciones formales
Anteriormente, utilizamos los términos arbitrariamente cercanos, arbitrariamente grandes y suficientemente grandes para definir límites en el infinito de manera informal. Aunque estos términos proporcionan descripciones precisas de los límites en el infinito, no son matemáticamente precisos. Aquí hay definiciones más formales de los límites en el infinito. Luego observamos cómo usar estas definiciones para probar resultados que involucran límites en el infinito.
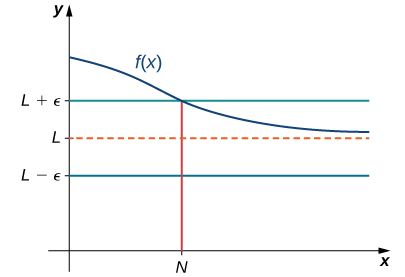
Definición 4.6.4 (Formal). Límite en el infinito
Decimos que una función f tiene un límite en el infinito, si existe un número real L tal que para todo ε > 0, existe un N > 0 tal que
| f(x) − L| < ε
para todo x > N. En ese caso, escribimos
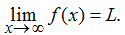
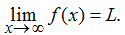
(ver Figura 4.25).
Decimos que una función f tiene un límite en infinito negativo si existe un número real L tal que para todo ε > 0, existe N < 0 tal que
| f(x) − L| < ε
para todo x < N. En ese caso, escribimos



Ahora dirigimos nuestra atención a una definición más precisa para un límite infinito en el infinito.
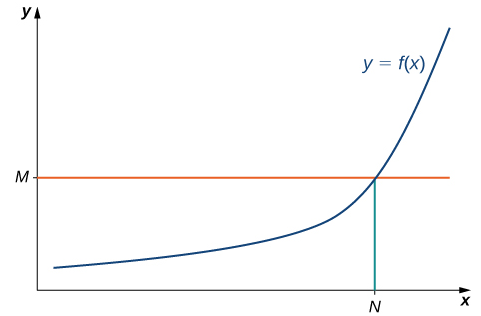
Definición 4.6.5 (Formal). Límite infinito en el infinito
Decimos que una función f tiene un límite infinito en el infinito y escribimos
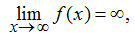
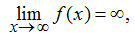
si para todo M > 0, existe un N > 0 tal que
f(x) > M
para todo x > N
(ver Figura 4.26).
Decimos que una función tiene un límite infinito negativo en el infinito y escribimos
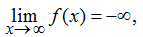
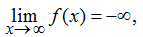
si para todo M < 0, existe un N > 0 tal que
f(x) < M
para todo x > N.
Del mismo modo, podemos definir límites cuando x → −∞.


Hola tengo el siguiente ejercicio
Lim. (1+a/x)^x
x-> ∞
Dónde a> 1
Debo calcular el límite por aproximación a la izquierda el límite me da e^a ahora mi pregunta es si cambio los valores de a el límite cambia según el enunciado, si tomo arbitrariamente un calor para a el límite por decir a= 4 la tabla si se puede calcular, la pregunta es sí puedo hacer eso??
Hola Martín.
Por supuesto que si.
Lim (1+a/x)^x
x-> ∞
es e^a
Y
Lim (1+4/x)^x
x-> ∞
es e^4
Y
Lim (1+215/x)^x
x-> ∞
es e^215
.
.
.
Saludos!
Hola, me puede explicar de manera sencilla cual es la relaciona entre los límites al infinito y limites infinitos con las asíntotas verticales y horizontales de las funciones. Por favor
Hola Marcela. Existen tres tipos de asíntotas: Horizontales, verticales y oblicuas.
Asíntotas horizontales: Si el límite de una función cuando la variable independiente x tiende al infinito es un valor constante se dice que la función tiene una asíntota horizontal. Por ejemplo, en la función f(x) = 1/x, cuando x tiende a más infinito, la función la función f tiende a 0; por lo tanto, y = 0 es una asíntota horizontal de f.
Asíntotas verticales: Si una función tiende a infinito cuando la variable independiente tiende a un valor constante, x = a, se dice que la función tiene una asíntota vertical. Por ejemplo, en la función f(x) = 1/(x+1), cuando x tiende a −1 por la derecha la función tiende a +∞; por lo tanto, x = –1 es una asíntota vertical de f.
Asíntotas oblicuas: En las funciones racionales impropias, donde el grado del numerador es una unidad mayor que el grado del denominador, ocurren asíntotas oblicuas. Estas asíntotas se obtienen efectuando la división de los polinomios, el cociente, que es una función lineal, es la asíntota oblicua. Por ejemplo, en la función f(x) = (x³ + x + 1)/(x² + 1) = x + 1/(x² + 1), y = x es una asíntota oblicua.
Hola
Hola María
¿Qué necesita, en qué le puedo colaborar? 👀👍
Saludos! 😺
Hola a todos, los contenidos proporcionados en este sitio web son realmente impresionantes para el aprendizaje de las personas interesadas en el Cálculo infinitesimal, sigan con el buen trabajo compañeros.