| 2. Límites y continuidad | 2.3 Propiedades de los límites de una función |
Leyes de límites aplicadas a límites unilaterales
Volvamos ahora a los límites unilaterales. Las modificaciones simples en las leyes de límites nos permiten aplicarlas a límites unilaterales. Por ejemplo, para aplicar las leyes de límite a un límite de la forma limx → a− h(x), requerimos que la función h(x) se defina en un intervalo abierto de la forma (b, a); para un límite de la forma limx → a+ h(x), requerimos que la función h(x) se defina en un intervalo abierto de la forma (a, c). El ejemplo 2.3_9 ilustra este punto.
EJEMPLO ILUSTRATIVO 2.3_9. Evaluación de un límite unilateral utilizando las leyes de límites
Evalúe cada uno de los siguientes límites, si es posible.


Solución
La figura 2.3_2 ilustra la función f (x) = √(x − 3) y ayuda a comprender estos límites.
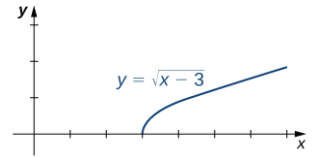

a. La función f (x) = √(x − 3) se define en el intervalo [3, + ∞). Como esta función no está definida a la izquierda de 3, no podemos aplicar las leyes de límite para calcular limx → 3− √(x − 3). De hecho, dado que f (x) = √(x − 3) no está definido a la izquierda de 3, limx → 3− √(x − 3) no existe.
b. Dado que f (x) = √(x − 3) se define a la derecha de 3, las leyes de límite se aplican a limx → 3+ √(x − 3). Al aplicar estas leyes de límite obtenemos limx → 3+ √(x − 3) = 0.
En el ejemplo 2.3_10 observamos los límites unilaterales de una función definida por partes y usamos estos límites para sacar una conclusión sobre un límite bilateral de la misma función.
EJEMPLO ILUSTRATIVO 2.3_10. Evaluación de un límite bilateral usando las leyes de límite
Para


evalúe cada uno de los siguientes límites:


Solución:
La figura 2.3_3 ilustra la función f (x) y ayuda a comprender estos límites.


a. Dado que f (x) = 4x − 3 para todas las x en (−∞, 2), reemplace f (x) en el límite con 4x − 3 y aplique las leyes de límite:


b. Dado que f (x) = (x − 3)² para todo x en (2, + ∞), reemplace f (x) en el límite con (x − 3) 2 y aplique las leyes de límite:


c. Como limx → 2− f (x) = 5 y limx → 2+ f (x) = 1, concluimos que limx → 2 f (x) no existe.
Ejercicio de control 2.3_7


Ahora dirigimos nuestra atención a evaluar un límite de la forma


donde


y


Es decir, f (x) / g (x) tiene la forma K / 0, K ≠ 0 en a.
EJEMPLO ILUSTRATIVO 2.3_11. Evaluación de un límite de la forma K / 0, K ≠ 0. Usando las leyes de límite
Evaluar


Solución
Paso 1. Después de sustituir en x = 2, vemos que este límite tiene la forma −1/0. Es decir, cuando x se acerca a 2 desde la izquierda, el numerador se acerca a −1; y el denominador se aproxima a 0. En consecuencia, la magnitud de


se vuelve infinito. Para tener una mejor idea de cuál es el límite, necesitamos factorizar el denominador:


Paso 2. Dado que x − 2 es la única parte del denominador que es cero cuando 2 está sustituido, separamos 1 / (x − 2) del resto de la función:


Paso 3. Los límites unilaterales por la izquierda dan


Por lo tanto, el producto de (x − 3) / x y 1 / (x − 2) tiene un límite de + ∞:


Ejercicio de control 2.3_8


El teorema de compresión (estricción)
Las técnicas que hemos desarrollado hasta ahora funcionan muy bien para las funciones algebraicas, pero aún no podemos evaluar los límites de las funciones trigonométricas básicas. El siguiente teorema, llamado teorema de compresión, resulta muy útil para establecer límites trigonométricos básicos. Este teorema nos permite calcular límites “exprimiendo” una función, con un límite, en un punto a, que es desconocido, entre dos funciones que tienen un límite común conocido en a. La figura 2.3_4 ilustra esta idea.
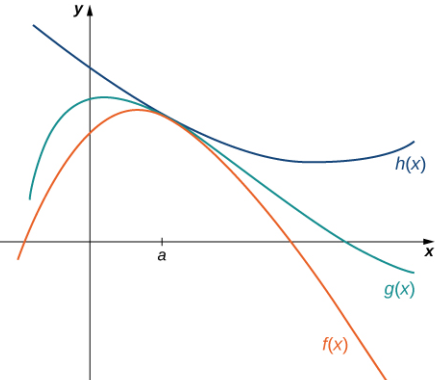

Figura 2.3_4 El teorema de compresión se aplica cuando f (x) ≤ g(x) ≤ h(x) y limx → a f (x) = limx → a h(x).
TEOREMA 2.3.1 El teorema de compresión o estricción
|
Sean las funciones f (x), g(x) y h(x) definidas para todo x ≠ a en un intervalo abierto que contenga a a. Si
para todo x ≠ a en un intervalo abierto que contiene a a y
donde L es un número real, entonces
|
EJEMPLO ILUSTRATIVO 2.3_12. Aplicando el teorema de compresión
Aplique el teorema de compresión para evaluar limx → 0 xcos x.
Solución:
Como −1 ≤ cosx ≤ 1 para todas las x, tenemos -| x | ≤ xcosx ≤ | x |. Como limx → 0 (-| x |) = 0 = limx → 0 | x |, a partir del teorema de compresión, obtenemos limx → 0 xcosx = 0. Las gráficas de f (x) = -| x |, g(x) = xcosx y h(x) = | x | se muestran en la figura 2.3_5.


Ejercicio de control 2.3_9
Utilice el teorema de la compresión para evaluar límx → 0 x2sen(1/x).
Ahora usamos el teorema de compresión para abordar varios límites muy importantes. Aunque esta discusión es algo larga, estos límites resultan invaluables para el desarrollo del material tanto en la siguiente sección como en el próximo capítulo. El primero de estos límites es limθ → 0senθ. Considere el círculo unitario que se muestra en la figura 2.3_6. En la figura, vemos que senθ es la coordenada y en el círculo unitario y corresponde al segmento de recta que se muestra en azul. La medida en radianes del ángulo θ es la longitud del arco que subtiende en el círculo unitario. Por lo tanto, vemos que para 0 < θ < π/2,0 < senθ < θ.


Debido a que


mediante el uso del teorema de compresión, concluimos que


Para ver que también


observe que para −π/2 < θ < 0, 0 < −θ < π/2 y por lo tanto, 0 < sen (−θ) < – θ. En consecuencia, 0 <−senθ <−θ. Se sigue que 0 > senθ > θ. Una aplicación del teorema de compresión produce el límite deseado. Por lo tanto, desde
![]()
![]()
se concluye que


Luego, usando la identidad


para −π/2 < θ < π/2, vemos que


Ahora echamos un vistazo a un límite que juega un papel importante en capítulos posteriores, a saber, limθ → 0 (senθ)/θ.
Para evaluar este límite, usamos el círculo unitario de la figura 2.3_7. Observe que esta figura agrega un triángulo adicional a la Figura 2.3_6. Vemos que la longitud del lado opuesto del ángulo θ en este nuevo triángulo es tanθ. Por lo tanto, vemos que para 0 < θ < π/2, senθ < θ < tanθ.
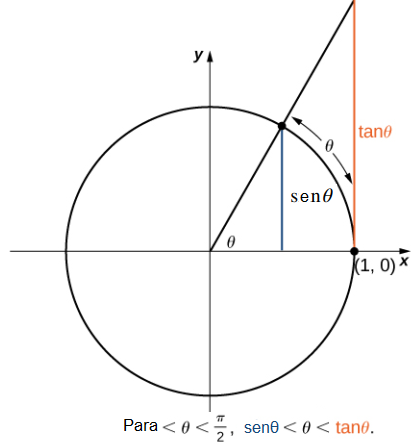

Al dividir por senθ en todas las partes de la desigualdad, obtenemos


Equivalentemente tenemos


Como limθ → 0+ 1 = 1 = limθ → 0+ cosθ, concluimos que limθ → 0+ senθ/θ = 1. Al aplicar una manipulación similar a la utilizada para demostrar que limθ → 0− senθ = 0, podemos mostrar que limθ → 0− senθ/θ = 1. Así,
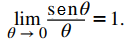
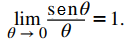
En el ejemplo 2.3_13 usamos este límite para establecer que
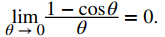
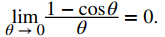
Este límite también resulta útil en capítulos posteriores.
EJEMPLO ILUSTRATIVO 2.3_13. Evaluación de un límite trigonométrico importante
Evaluar


Solución:
En el primer paso, multiplicamos por el conjugado para que podamos usar una identidad trigonométrica para convertir el coseno en el numerador en un seno:


Por lo tanto,
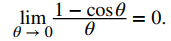
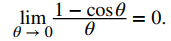
Ejercicio de control 2.3_10
Evalúe limθ → 0 (1 − cosθ)/senθ.
Ejercicios resueltos
Evaluar el siguiente límite unilateral
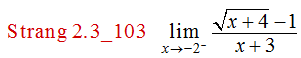
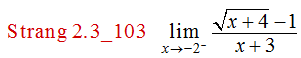



Excelente material. Muchas gracias.
Con mucho gusto 😺👍
Buenas tardes
Muy buen aporte.
Les envío un comentario sobre “CÁLCULO 21”
2.3 LAS LEYES DE LÍMITES: Objetivos de aprendizaje
TEOREMA 2.3.2 Leyes de límites
Raiz:
Donde dice:
“para todo L si n es par
y para L>=0 si n es impar”
Debería decir:
“Para todo L si n es impar.
Para todo L>=0 si n es par.”
Muchas gracias
Hola Hugo
Gracias por el comentario.
Tiene toda la razón! Ya lo he corregido 👍
Era muy difícil darme cuenta de ese error! 😺👍