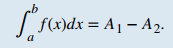Área y la integral definida

Cuando definimos la integral definida, eliminamos el requisito de que f (x) sea no negativa. Pero, ¿cómo interpretamos “el área bajo la curva” cuando f (x) es negativa?

Área neta con signo

Volvamos a la suma de Riemann. Considere, por ejemplo, la función f (x) = 2 − 2x² (que se muestra en la Figura 5.2_2) en el intervalo [0, 2]. Tome n = 8 y elija {xᵢ*} como el punto final izquierdo de cada intervalo. Construya un rectángulo en cada subintervalo de altura f (xᵢ*) y ancho Δx. Cuando f (xᵢ*) es positivo, el producto f (xᵢ*)Δx representa el área del rectángulo, como antes. Sin embargo, cuando f (xᵢ*) es negativo, el producto f (xᵢ*)Δx representa el negativo del área del rectángulo. La suma de Riemann se convierte en

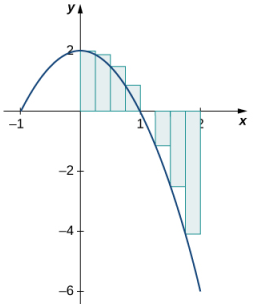
Figura 5.2_2 Para una función que es parcialmente negativa, la suma de Riemann es el área de los rectángulos sobre el eje x menos el área de los rectángulos debajo del eje x.

Tomando el límite cuando n → ∞, la suma de Riemann se acerca al área entre la curva sobre el eje x y el eje x, menos el área entre la curva debajo del eje x y el eje x, como se muestra en la Figura 5.2_3 . Entonces,

La cantidad A₁ − A₂ se llama área neta con signo.

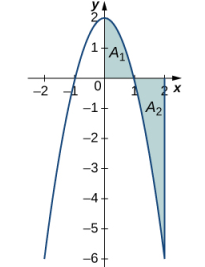
Figura 5.2_3 En el límite, la integral definida es igual al área A₁ menos el área A₂, o el área neta con signo.

Observe que el área neta con signo puede ser positiva, negativa o cero. Si el área sobre el eje x es más grande, el área neta con signo es positiva. Si el área debajo del eje x es más grande, el área neta con signo es negativa. Si las áreas arriba y debajo del eje x son iguales, el área neta con signo es cero.

Ejemplo ilustrativo 5.2_3. Encontrar un área neta con signo

Encuentre el área neta con signo entre la curva de la función f (x) = 2x y el eje x sobre el intervalo [−3, 3].

Solución:
La función produce una línea recta que forma dos triángulos: uno de x = −3 a x = 0 y el otro de x = 0 a x = 3 (Figura 5.2_4). Usando la fórmula geométrica para el área de un triángulo, A = bh/2, el área del triángulo A₁, sobre el eje, es

donde 3 es la base y 2(3) = 6 es la altura. El área del triángulo A₂, debajo del eje, es

donde 3 es la base y 6 es la altura. Por lo tanto, el área neta es

Figura 5.2_4 El área sobre la curva y debajo del eje x es igual al área debajo de la curva y sobre el eje x.

Análisis

Si A₁ es el área sobre el eje x y A₂ es el área debajo del eje x, entonces el área neta es A₁ − A₂. Como las áreas de los dos triángulos son iguales, el área neta es cero. ◊

Área total

Una aplicación de la integral definida es encontrar el desplazamiento cuando se da una función de velocidad. Si v(t) representa la velocidad de un objeto móvil en función del tiempo, entonces el área debajo de la curva nos dice qué tan lejos está el objeto de su posición original. Esta es una aplicación muy importante de la integral definida, y la examinamos con más detalle más adelante en este capítulo. Por ahora, solo veremos algunos conceptos básicos para tener una idea de cómo funciona esto al estudiar velocidades constantes.

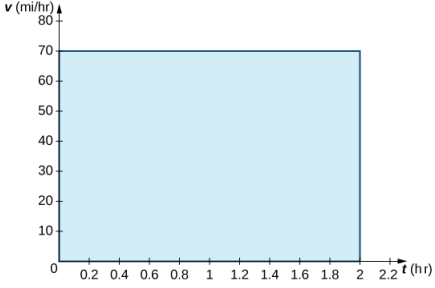
Cuando la velocidad es constante, el área bajo la curva es solo velocidad por tiempo. Esta idea ya es muy familiar. Si un automóvil se aleja de su posición inicial en línea recta a una velocidad de 75 mph durante 2 horas, entonces está a 150 millas de su posición original (Figura 5.2_5). Usando notación integral, tenemos

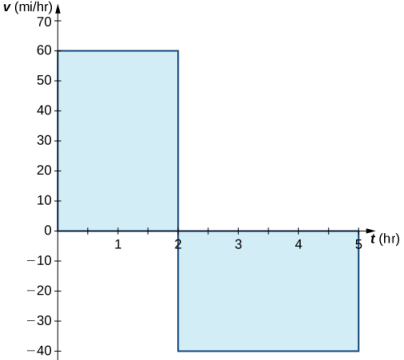
En el contexto del desplazamiento, el área neta con signo nos permite tener en cuenta la dirección. Si un automóvil viaja hacia el norte a una velocidad de 60 mph durante 2 horas, está a 120 millas al norte de su posición inicial. Si el automóvil gira y viaja hacia el sur a una velocidad de 40 mph durante 3 horas, volverá a su posición inicial (Figura 5.2_6). Nuevamente, usando notación integral, tenemos

En este caso el desplazamiento es cero.

Supongamos que queremos saber qué tan lejos viaja el móvil en general, independientemente de la dirección. En este caso, queremos saber el área entre la curva y el eje x, independientemente de si esa área está por encima o por debajo del eje. Esto se llama el área total.

Gráficamente, es más fácil pensar en calcular el área total sumando las áreas sobre el eje y las áreas debajo del eje (en lugar de restar las áreas debajo del eje, como hicimos con el área neta con signo). Para lograr esto matemáticamente, usamos la función de valor absoluto. Por lo tanto, la distancia total recorrida por el móvil es

Al reunir estas ideas formalmente, establecemos las siguientes definiciones.

DEFINICIÓN. Área neta con signo y área total

Sea f (x) una función integrable definida en un intervalo [a, b]. Deje que A1 represente el área entre f (x) y el eje x que se encuentra sobre el eje y deje que A2 represente el área entre f (x) y el eje x que se encuentra debajo del eje. Luego, el área neta con signo entre f (x) y el eje x viene dada por El área total entre f (x) y el eje x viene dada por

Ejemplo ilustrativo 5.2_4. Encontrar el área total

Halle el área total entre f (x) = x − 2 y el eje x sobre el intervalo [0, 6].

Solución:
Calcule la intersección x como (2, 0) (establezca y = 0, resuelva para x). Para encontrar el área total, tome el área debajo del eje x sobre el subintervalo [0, 2] y agréguela al área sobre el eje x en el subintervalo [2, 6] (Figura 5.2_7).

Se tiene que

Luego, usando la fórmula para el área de un triángulo, obtenemos

El área total, entonces, es

◊