| 5. La integral y Técnicas de integración | Ejercicios propuestos para el Capítulo 5.2 |
5.2 La integral definida
Objetivos de aprendizaje:
5.2.1. Indique la definición de la integral definida.
5.2.2. Explicar los términos integrando, límites de integración y variable de integración.
5.2.3. Explica cuándo una función es integrable.
5.2.4. Describa la relación entre la integral definida y el área neta.
5.2.5. Use la geometría y las propiedades de integrales definidas para evaluarlas.
5.2.6. Calcular el valor promedio de una función.
En la sección anterior definimos el área bajo una curva en términos de sumas de Riemann:
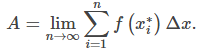
Sin embargo, esta definición vino con restricciones. Requerimos que f (x) fuera continua y no negativa. Lamentablemente, los problemas del mundo real no siempre cumplen con estas restricciones. En esta sección, veremos cómo aplicar el concepto del área bajo la curva a un conjunto más amplio de funciones mediante el uso de la integral definida.
Definición y notación
La integral definida generaliza el concepto del área bajo una curva. Levantamos los requisitos de que f (x) sea continua y no negativa, y definimos la integral definida de la siguiente manera.
DEFINICIÓN 5.2_1. La integral definida
Si \( f(x) \) es una función definida en un intervalo \( [a, b] \), la integral definida de \( f \) de \( a \) a \( b \) viene dada por
\[ \int_a^b f(x) \, dx = \lim_{n \to \infty} \sum_{i=1}^n f(x_i^*) \Delta x, \]
siempre que exista el límite. Si este límite existe, se dice que la función \( f(x) \) es integrable en \( [a, b] \), o es una función integrable. ♦
El símbolo de integral en la definición anterior debería ser familiar. Hemos visto una notación similar en el capítulo sobre Aplicaciones de las derivadas, donde utilizamos el símbolo de la integral indefinida (sin las letras a y b arriba y abajo) para representar una antiderivada. Aunque la notación para integrales indefinidas puede ser similar a la notación para una integral definida, no son lo mismo. Una integral definida es un número. Una integral indefinida es una familia de funciones. Más adelante en este capítulo examinamos cómo se relacionan estos conceptos. Sin embargo, siempre se debe prestar mucha atención a la notación para que sepamos si estamos trabajando con una integral definida o una integral indefinida.
La notación de la integral se remonta a finales del siglo XVII y es una de las contribuciones de Gottfried Wilhelm Leibniz, quien a menudo se considera el codescubridor del cálculo, junto con Isaac Newton. El símbolo de integración ∫ es una S alargada, que sugiere sigma o suma. En una integral definida, arriba y abajo del símbolo de integración están escritas las letras a y b, son los límites del intervalo [a, b]. Los números a y b son x-valores y se denominan límites de integración; específicamente, a es el límite inferior y b es el límite superior. Para aclarar, estamos usando la palabra límite de dos maneras diferentes en el contexto de la integral definida. Primero, hablamos sobre el límite de una suma como n → ∞. En segundo lugar, los límites de la región se denominan límites de integración.
Llamamos a la función f (x) el integrando, y el dx indica que f (x) es una función con respecto a x, llamada variable de integración. Tenga en cuenta que, como el índice en una suma, la variable de integración es una variable ficticia y no tiene ningún impacto en el cálculo de la integral. Podríamos usar cualquier variable que nos guste como variable de integración:

Anteriormente, discutimos el hecho de que si f (x) es continua en [a, b], entonces el límite
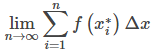
existe y es único. Esto lleva al siguiente teorema, que afirmamos sin pruebas.
TEOREMA 5.2.1. Las funciones continuas son integrables
Si f (x) es continua en [a, b], entonces f es integrable en [a, b]. ♦
Las funciones que no son continuas en [a, b] aún pueden ser integrables, dependiendo de la naturaleza de las discontinuidades. Por ejemplo, las funciones con un número finito de discontinuidades de salto en un intervalo cerrado son integrables.
También vale la pena señalar aquí que hemos conservado el uso de una partición regular en las sumas de Riemann. Esta restricción no es estrictamente necesaria. Cualquier partición puede usarse para formar una suma de Riemann. Sin embargo, si se usa una partición no regular para definir la integral definida, no es suficiente tomar el límite ya que el número de subintervalos va al infinito. En cambio, debemos tomar el límite para cuando el ancho del subintervalo más grande tiende a cero. Esto introduce una notación un poco más compleja en nuestros límites y hace que los cálculos sean más difíciles sin realmente obtener mucha información adicional, por lo que nos quedamos con particiones regulares para las sumas de Riemann.
Ejemplo ilustrativo 5.2_1. Evaluar una integral usando la definición
Use la definición de la integral definida para evaluar
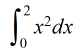
Use una aproximación del punto final derecho para generar la suma de Riemann.
Solución:
Primero debemos establecer una suma de Riemann. Con base en los límites de integración, tenemos a = 0 y b = 2. Para i = 0, 1, 2,…, n, sea P = {xᵢ} una partición regular de [0, 2]. Entonces
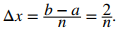
Como estamos utilizando una aproximación del punto final derecho para generar sumas de Riemann, para cada i, necesitamos calcular el valor de la función en el punto final derecho del intervalo [xᵢ₋₁, xᵢ]. El punto final derecho del intervalo es xᵢ], y dado que P es una partición regular,
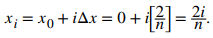
Por lo tanto, el valor de la función en el punto final derecho del intervalo es

Entonces la suma de Riemann toma la forma
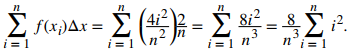
Usando la fórmula de suma para
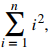
se tiene que
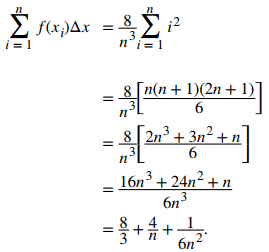
Cómo, para calcular la integral definida, necesitamos tomar el límite cuando n → ∞. Obtenemos

♦
Ejercicio de control 5.2.1
Use la definición de la integral definida para evaluar \( \int_0^3 (2x – 1) \, dx \). Use una aproximación de punto final derecho para generar la suma de Riemann. ♦
Evaluación de integrales definidas
Evaluar integrales definidas de esta manera puede ser bastante tedioso debido a la complejidad de los cálculos. Más adelante en este capítulo desarrollamos técnicas para evaluar integrales definidas sin tomar límites de sumas de Riemann. Sin embargo, por ahora, podemos confiar en el hecho de que las integrales definidas representan el área bajo la curva, y podemos evaluar integrales definidas mediante el uso de fórmulas geométricas para calcular esa área. Hacemos esto para confirmar que las integrales definidas, de hecho, representan áreas, por lo que podemos discutir qué hacer en el caso de que una curva de una función caiga por debajo del eje x.
Ejemplo ilustrativo 5.2_2. Uso de fórmulas geométricas para calcular integrales definidas
Use la fórmula para el área de un círculo para evaluar

Solución:
La función describe un semicírculo con radio 3. Para encontrar debemos encontrar el área debajo de la curva sobre el intervalo [3, 6]. La fórmula para el área de un círculo es A = πr². El área de un semicírculo es solo la mitad del área de un círculo, o A = (1/2)πr². El área sombreada en la Figura 5.2_1 cubre la mitad del semicírculo, o A = (1/4)πr². Así,
debemos encontrar el área debajo de la curva sobre el intervalo [3, 6]. La fórmula para el área de un círculo es A = πr². El área de un semicírculo es solo la mitad del área de un círculo, o A = (1/2)πr². El área sombreada en la Figura 5.2_1 cubre la mitad del semicírculo, o A = (1/4)πr². Así,
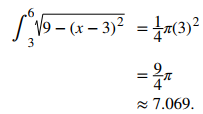
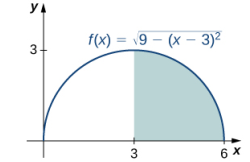
Figura 5.2_1 El valor de la integral de la función f (x) durante el intervalo [3, 6] es el área de la región sombreada. ♦
Ejercicio de control 5.2.2
Use la fórmula para el área de un trapezoide para evaluar \( \int_2^4 (2x + 3) \, dx \). ♦
Área y la integral definida
Cuando definimos la integral definida, eliminamos el requisito de que f (x) sea no negativa. Pero, ¿cómo interpretamos “el área bajo la curva” cuando f (x) es negativa?
Área neta con signo
Volvamos a la suma de Riemann. Considere, por ejemplo, la función f (x) = 2 − 2x² (que se muestra en la Figura 5.2_2) en el intervalo [0, 2]. Tome n = 8 y elija {xᵢ*} como el punto final izquierdo de cada intervalo. Construya un rectángulo en cada subintervalo de altura f (xᵢ*) y ancho Δx. Cuando f (xᵢ*) es positivo, el producto f (xᵢ*)Δx representa el área del rectángulo, como antes. Sin embargo, cuando f (xᵢ*) es negativo, el producto f (xᵢ*)Δx representa el negativo del área del rectángulo. La suma de Riemann se convierte en

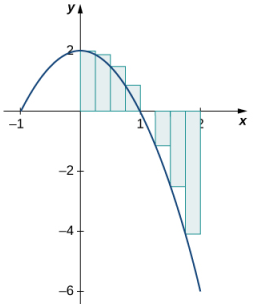
Figura 5.2_2 Para una función que es parcialmente negativa, la suma de Riemann es el área de los rectángulos sobre el eje x menos el área de los rectángulos debajo del eje x.
Tomando el límite cuando n → ∞, la suma de Riemann se acerca al área entre la curva sobre el eje x y el eje x, menos el área entre la curva debajo del eje x y el eje x, como se muestra en la Figura 5.2_3 . Entonces,

La cantidad A1 − A2 se llama área neta con signo.
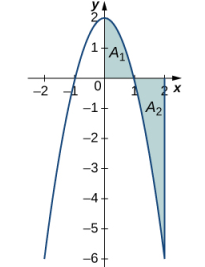
Figura 5.2_3 En el límite, la integral definida es igual al área A1 menos el área A2, o el área neta con signo.
Observe que el área neta con signo puede ser positiva, negativa o cero. Si el área sobre el eje x es más grande, el área neta con signo es positiva. Si el área debajo del eje x es más grande, el área neta con signo es negativa. Si las áreas arriba y debajo del eje x son iguales, el área neta con signo es cero.
Ejemplo ilustrativo 5.2_3. Encontrar un área neta con signo
Encuentre el área neta con signo entre la curva de la función f (x) = 2x y el eje x sobre el intervalo [−3, 3].
Solución:
La función produce una línea recta que forma dos triángulos: uno de x = −3 a x = 0 y el otro de x = 0 a x = 3 (Figura 5.2_4). Usando la fórmula geométrica para el área de un triángulo, A = bh/2, el área del triángulo A1, sobre el eje, es

donde 3 es la base y 2(3) = 6 es la altura. El área del triángulo A2, debajo del eje, es

donde 3 es la base y 6 es la altura. Por lo tanto, el área neta es

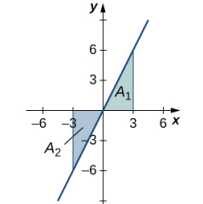
Figura 5.2_4 El área sobre la curva y debajo del eje x es igual al área debajo de la curva y sobre el eje x. ♦
Análisis
Si A1 es el área sobre el eje x y A2 es el área debajo del eje x, entonces el área neta es A1 − A2. Como las áreas de los dos triángulos son iguales, el área neta es cero. ♦
Ejercicio de control 5.2.3
Encuentre el área neta con signo de \( f(x) = x – 2 \) sobre el intervalo \( [0, 6] \), ilustrado en la siguiente imagen.
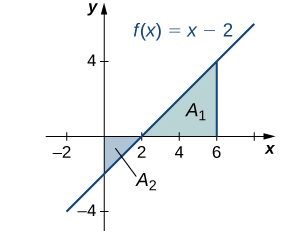
♦
Área total
Una aplicación de la integral definida es encontrar el desplazamiento cuando se da una función de velocidad. Si v(t) representa la velocidad de un objeto móvil en función del tiempo, entonces el área debajo de la curva nos dice qué tan lejos está el objeto de su posición original. Esta es una aplicación muy importante de la integral definida, y la examinamos con más detalle más adelante en este capítulo. Por ahora, solo veremos algunos conceptos básicos para tener una idea de cómo funciona esto al estudiar velocidades constantes.
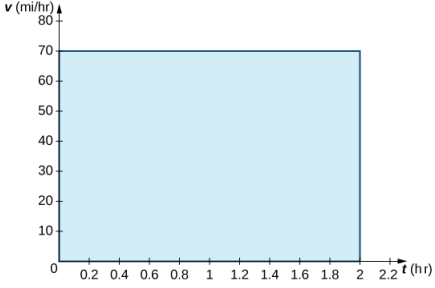
Cuando la velocidad es constante, el área bajo la curva es solo velocidad por tiempo. Esta idea ya es muy familiar. Si un automóvil se aleja de su posición inicial en línea recta a una velocidad de 75 mph durante 2 horas, entonces está a 150 millas de su posición original (Figura 5.2_5). Usando notación integral, tenemos

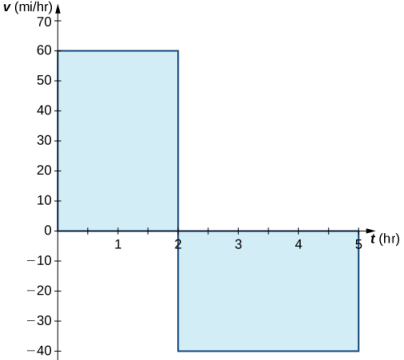
En el contexto del desplazamiento, el área neta con signo nos permite tener en cuenta la dirección. Si un automóvil viaja hacia el norte a una velocidad de 60 mph durante 2 horas, está a 120 millas al norte de su posición inicial. Si el automóvil gira y viaja hacia el sur a una velocidad de 40 mph durante 3 horas, volverá a su posición inicial (Figura 5.2_6). Nuevamente, usando notación integral, tenemos

En este caso el desplazamiento es cero.
Supongamos que queremos saber qué tan lejos viaja el móvil en general, independientemente de la dirección. En este caso, queremos saber el área entre la curva y el eje x, independientemente de si esa área está por encima o por debajo del eje. Esto se llama el área total.
Gráficamente, es más fácil pensar en calcular el área total sumando las áreas sobre el eje y las áreas debajo del eje (en lugar de restar las áreas debajo del eje, como hicimos con el área neta con signo). Para lograr esto matemáticamente, usamos la función de valor absoluto. Por lo tanto, la distancia total recorrida por el móvil es

Al reunir estas ideas formalmente, establecemos las siguientes definiciones.
DEFINICIÓN. Área neta con signo y área total
Sea \( f(x) \) una función integrable definida en un intervalo \( [a, b] \). Sea \( A_1 \) representar el área entre \( f(x) \) y el eje x que se encuentra arriba del eje y sea \( A_2 \) representar el área entre \( f(x) \) y el eje x que se encuentra debajo del eje. Entonces, el área neta con signo entre \( f(x) \) y el eje x está dada por
\[ \int_a^b f(x) \, dx = A_1 – A_2. \]
El área total entre \( f(x) \) y el eje x está dada por
\[ \int_a^b |f(x)| \, dx = A_1 + A_2. \]
♦
Ejemplo ilustrativo 5.2_4. Encontrar el área total
Halle el área total entre f (x) = x − 2 y el eje x sobre el intervalo [0, 6].
Solución:
Calcule la intersección x como (2, 0) (establezca y = 0, resuelva para x). Para encontrar el área total, tome el área debajo del eje x sobre el subintervalo [0, 2] y agréguela al área sobre el eje x en el subintervalo [2, 6] (Figura 5.2_7).

Figura 5.2_7 El área total entre la recta y el eje x en [0, 6] es A2 más A1.
Se tiene que

Luego, usando la fórmula para el área de un triángulo, obtenemos

El área total, entonces, es

♦
Ejercicio de control 5.2.4
Encuentra el área total entre la función f (x) = 2x y el eje x sobre el intervalo [−3, 3]. ♦
Propiedades de la integral definida
Las propiedades de las integrales indefinidas se aplican también a las integrales definidas. Las integrales definidas también tienen propiedades que se relacionan con los límites de la integración. Estas propiedades, junto con las reglas de integración que examinamos más adelante en este capítulo, nos ayudan a manipular expresiones para evaluar integrales definidas.
REGLA 5.2_1: PROPIEDADES DE LA INTEGRAL DEFINIDA
- Si los límites de integración son los mismos, la integral es solo una recta vertical y no contiene área:
\[ \int_a^a f(x) \, dx = 0 \]
- Si los límites de integración se invierten, coloque un signo negativo antes de la integral:
\[ \int_b^a f(x) \, dx = – \int_a^b f(x) \, dx \]
- La integral de una suma es la suma de las integrales:
\[ \int_a^b (f(x) + g(x)) \, dx = \int_a^b f(x) \, dx + \int_a^b g(x) \, dx \]
- La integral de una diferencia es la diferencia de las integrales:
\[ \int_a^b (f(x) – g(x)) \, dx = \int_a^b f(x) \, dx – \int_a^b g(x) \, dx \]
- Sea \( c \) una constante. La integral del producto de una constante y una función es igual a la integral de la función multiplicada por la constante:
\[ \int_a^b cf(x) \, dx = c \int_a^b f(x) \, dx \]
- Aunque la siguiente fórmula normalmente se aplica cuando \( c \) está entre \( a \) y \( b \), la fórmula es válida para todos los valores de \( a \), \( b \) y \( c \), siempre que \( f(x) \) sea integrable en el intervalo más grande:
\[ \int_a^b f(x) \, dx = \int_a^c f(x) \, dx + \int_c^b f(x) \, dx \]
♦
Ejemplo ilustrativo 5.2_5. Usando las propiedades de la integral definida
Use las propiedades de la integral definida para expresar la integral definida de f (x) = – 3x³ + 2x + 2 sobre el intervalo [−2, 1] como la suma de tres integrales definidas.
Solución;
Usando notación integral, tenemos

De tal modo que, al aplicar las propiedades de la integral definida, se tiene que:

♦
Ejercicio de control 5.2.5
Use las propiedades de la integral definida para expresar la integral definida de \( f(x) = 6x^3 – 4x^2 + 2x – 3 \) sobre el intervalo \( [1, 3] \) como la suma de cuatro integrales definidas. ♦
Ejemplo ilustrativo 5.2_6. Usando las propiedades de la integral definida
Si se sabe que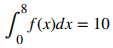 y que
y que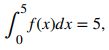 encuentra el valor de
encuentra el valor de
Solución:
Por la propiedad 6, se tiene

De tal modo que

♦
Ejercicio de control 5.2.6
Si se sabe que \( \int_1^5 f(x) \, dx = -3 \) y \( \int_2^5 f(x) \, dx = 4 \), encuentre el valor de \( \int_1^2 f(x) \, dx \). ♦
Propiedades de comparación de integrales
Una imagen a veces puede decirnos más acerca de una función que los resultados de los cálculos. La comparación de funciones por sus gráficas y por sus expresiones algebraicas a menudo puede dar una nueva visión del proceso de integración. Intuitivamente, podríamos decir que si una función f (x) está por encima de otra función g (x), entonces el área entre f (x) y el eje x es mayor que el área entre g(x) y el eje x. Esto es cierto dependiendo del intervalo durante el cual se realiza la comparación. Las propiedades de las integrales definidas son válidas si a < b, a = b, o a > b. Sin embargo, las siguientes propiedades se refieren solo al caso a ≤ b, y se utilizan cuando queremos comparar los tamaños de las integrales.
TEOREMA 5.2.2. Teorema de comparación
- Si \( f(x) \geq 0 \) para \( a \leq x \leq b \), entonces
\[ \int_a^b f(x) \, dx \geq 0. \]
- Si \( f(x) \geq g(x) \) para \( a \leq x \leq b \), entonces
\[ \int_a^b f(x) \, dx \geq \int_a^b g(x) \, dx. \]
- Si \( m \) y \( M \) son constantes tales que \( m \leq f(x) \leq M \) para \( a \leq x \leq b \), entonces
\[ m(b – a) \leq \int_a^b f(x) \, dx \leq M(b – a). \]
♦
Ejemplo ilustrativo 5.2_7. Comparar dos funciones sobre un intervalo dado
Compare f (x) = √(1 + x²) y g(x) = √(1 + x) en el intervalo [0, 1].
Solución:
Graficar estas funciones es necesario para comprender cómo se comparan durante el intervalo [0, 1]. Inicialmente, cuando se grafica en una calculadora gráfica, f (x) parece estar por encima de g(x) en todas partes. Sin embargo, en el intervalo [0, 1], los gráficos parecen coincidir. Necesitamos acercarnos para ver que, en el intervalo [0, 1], g(x) está por encima de f (x). Las dos funciones se cruzan en x = 0 y x = 1 (Figura 5.2_8).

Podemos ver en la figura que durante el intervalo [0, 1], g(x) ≥ f (x). Al comparar las integrales en el intervalo especificado [0, 1], también vemos que
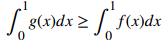
(Figura 5.2_9). El área delgada sombreada en rojo muestra cuánta diferencia hay entre estas dos integrales durante el intervalo [0, 1].
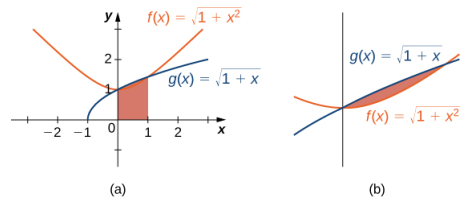
♦
Valor promedio de una función
A menudo necesitamos encontrar el promedio de un conjunto de números, como una calificación promedio en una prueba. Suponga que recibió los siguientes puntajes de los exámenes en su clase de álgebra: 89, 90, 56, 78, 100 y 69. Su calificación semestral es el promedio de los puntajes de los exámenes y desea saber qué calificación esperar. Podemos encontrar el promedio sumando todos los puntajes y dividiendo entre el número de puntajes. En este caso, hay seis puntajes de prueba. Así,
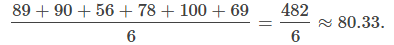
Por lo tanto, su calificación promedio es de aproximadamente 80.33, lo que se traduce en una B en la mayoría de las escuelas.
Supongamos, sin embargo, que tenemos una función v(t) que nos da la velocidad de un móvil en cualquier momento t, y queremos encontrar la velocidad promedio del móvil. La función v(t) adquiere un número infinito de valores, por lo que no podemos usar el proceso que acabamos de describir. Afortunadamente, podemos usar una integral definida para encontrar el valor promedio de una función como esta.
Supongamos que f (x) sea continua durante el intervalo [a, b] y que [a, b] se divida en n subintervalos de ancho Δx = (b − a)/n. Elija un representante xᵢ* en cada subintervalo y calcule f (xᵢ*) para i = 1, 2, …, n. En otras palabras, considere cada f (xᵢ*) como una muestra de la función sobre cada subintervalo. El valor promedio de la función puede ser aproximado como
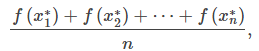
que es básicamente la misma expresión utilizada para calcular el promedio de valores discretos.
Pero sabemos que Δx = (b − a)/n, entonces n = (b − a)/Δx, y obtenemos
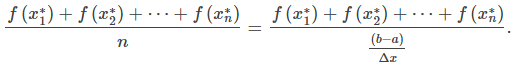
Siguiendo con el álgebra, el numerador es una suma que se representa como
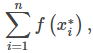
y estamos dividiendo por una fracción. Para dividir por una fracción, invierte el denominador y multiplica. Por lo tanto, un valor aproximado para el valor promedio de la función viene dado por
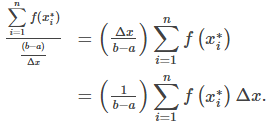
Esta es una suma de Riemann. Luego, para obtener el valor promedio exacto, tome el límite a medida que n va al infinito. Por lo tanto, el valor promedio de una función viene dado por

DEFINICIÓN. Valor promedio de una función
Sea \( f(x) \) una función continua en un intervalo cerrado \( [a, b] \). Entonces, el valor promedio de la función \( f(x) \) (o \( f_{\text{ave}} \) ) en \( [a, b] \) viene dado por
\( f_{\text{ave}} = \frac{1}{b – a} \int_a^b f(x) \, dx. \)
♦
Ejemplo ilustrativo 5.2_8. Encontrar el valor promedio de una función lineal
Encuentre el valor promedio de f (x) = x + 1 en el intervalo [0, 5].
Solución:
Primero, grafica la función en el intervalo establecido, como se muestra en la Figura 5.2_10.
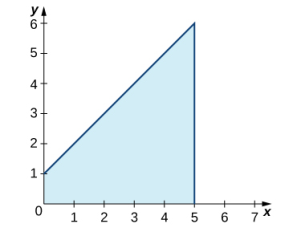
La región es un trapecio acostado de lado, por lo que podemos usar la fórmula del área para un trapecio A = h(a + b)/2, donde h representa la altura, y a y b representan los dos lados paralelos. Entonces,
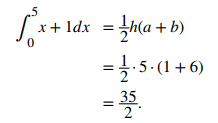
Por lo tanto, el valor promedio de la función es
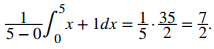
♦
Ejercicio de control 5.2.7
Encuentre el valor promedio de \( f(x) = 6 – 2x \) sobre el intervalo \( [0, 3] \). ♦
