| 5. La integral y Técnicas de integración | Ejercicios propuestos para el Capítulo 5.5 |
5.5 Integración por sustitución u
Objetivos de aprendizaje:
5.5.1 Utilice la sustitución u para evaluar integrales indefinidas.
5.5.2 Utilice la sustitución u para evaluar integrales definidas.
El teorema fundamental del cálculo nos dio un método para evaluar integrales sin usar sumas de Riemann. Sin embargo, el inconveniente de este método es que debemos ser capaces de encontrar una antiderivada, y esto no siempre es fácil. En esta sección examinamos una técnica, llamada integración por sustitución, para ayudarnos a encontrar antiderivadas. Específicamente, este método nos ayuda a encontrar antiderivadas cuando el integrando es el resultado de una derivada de la regla de la cadena.
Al principio, el enfoque del procedimiento de sustitución puede no parecer muy obvio. Sin embargo, es principalmente una tarea visual, es decir, el integrando le muestra qué hacer; se trata de reconocer la forma de la función. Entonces, ¿qué se supone que debemos ver? Estamos buscando un integrando de la forma f [g(x)]g′(x)dx. Por ejemplo, en la integral
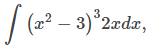
f (x) = x³, g(x) = x² − 3 y g′(x) = 2x. Entonces,

y vemos que nuestro integrando está en la forma correcta.
El método se llama sustitución porque sustituimos parte del integrando con la variable u y parte del integrando con du. También se conoce como cambio de variables porque estamos cambiando variables para obtener una expresión con la que es más fácil trabajar para aplicar las reglas de antiderivación.
TEOREMA 5.5.1. Sustitución u con integrales indefinidas
Sea \(u = g(x)\), donde \(g'(x)\) es continua en un intervalo, sea \(f(x)\) continua sobre el rango correspondiente de \(g\), y sea \(F(x)\) una antiderivada de \(f(x)\). Entonces,
\(\begin{aligned} \int f[g(x)] g'(x) dx &= \int f(u) du \\ &= F(u) + C \\ &= F(g(x)) + C. \end{aligned}\)
♦
Prueba
Deje f, g, u, y F como se especifica en el teorema. Entonces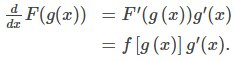 Integrando ambos lados con respecto a x, vemos que
Integrando ambos lados con respecto a x, vemos que Si ahora sustituimos u = g(x) e y = g′(x)dx, obtenemos
Si ahora sustituimos u = g(x) e y = g′(x)dx, obtenemos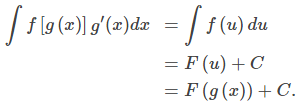 ♦
♦
Volviendo al problema que vimos originalmente, dejamos u = x² − 3 y luego du = 2xdx. Reescribe la integral en términos de u:

Usando la regla de la potencia para integrales, tenemos

Sustituya la expresión original por x en la solución:

Podemos generalizar el procedimiento en la siguiente estrategia de resolución de problemas.
ESTRATEGIA DE RESOLUCIÓN DE PROBLEMAS: INTEGRACIÓN POR SUSTITUCIÓN u
- Mire cuidadosamente el integrando y seleccione una expresión g(x) dentro del integrando para establecer igual a u. Seleccionemos g(x) tal que g′(x) también sea parte del integrando.
- Sustituya u = g(x) y du = g′(x)dx. en la integral.
- Ahora deberíamos poder evaluar la integral con respecto a u. Si no se puede evaluar la integral, debemos regresar y seleccionar una expresión diferente para usar como u.
- Evalúa la integral en términos de u.
- Escribe el resultado en términos de x y la expresión g(x). ♦
EJEMPLO ILUSTRATIVO 5.5_1. Usar sustitución u para encontrar una antiderivada
Usa la sustitución para encontrar la antiderivada

Solución:
El primer paso es elegir una expresión para u. Elegimos u = 3x² + 4 porque entonces du = 6xdx, y ya tenemos du en el integrando. Escribe la integral en términos de u:

Recuerde que du es la diferencial de la expresión elegida para u, independientemente de lo que esté dentro del integrando. Ahora podemos evaluar la integral con respecto a u:

Análisis
Podemos verificar nuestra respuesta tomando la derivada del resultado de la integración. Deberíamos obtener el integrando. Al elegir un valor para C de 1, dejamos y = (1/5)(3x² + 4)⁵ + 1. Tenemos

Esta es exactamente la expresión con la que comenzamos dentro del integrando. ♦
Ejercicio de control 5.5.1
Usa la sustitución u para encontrar la antiderivada  ♦
♦
A veces necesitamos ajustar las constantes en nuestra integral si no coinciden exactamente con las expresiones que estamos sustituyendo.
EJEMPLO ILUSTRATIVO 5.5_2. Usar sustitución u con modificación del integrando
Usa la sustitución para encontrar

Solución:
Reescribe la integral como

Sea u = z² − 5 y du = 2zdz. Ahora tenemos un problema porque du = 2zdz y la expresión original solo tiene zdz. Tenemos que alterar nuestra expresión para du o la integral en u será dos veces más grande de lo que debería ser. Si multiplicamos ambos lados de la ecuación du = 2zdz por 1/2. podemos resolver este problema. Así,

Escribe la integral en términos de u, pero saca el 1/2 fuera del símbolo de integración:

Integre la expresión en u:
 ♦
♦
Ejercicio de control 5.5.2
Usa la sustitución u para encontrar la antiderivada  ♦
♦
EJEMPLO ILUSTRATIVO 5.5_3. Uso de sustitución u con integrales de funciones trigonométricas
Usar sustitución u para evaluar la integral

Solución:
Sabemos que la derivada del cost es −sent, así que configuramos u =cost. Entonces du = −sent dt. Sustituyendo en la integral, tenemos

Evaluando la integral, obtenemos

Para dar la respuesta de la integral, restituimos a la variable original t, para obtener
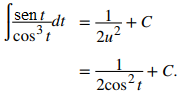 ♦
♦
Ejercicio de control 5.5.3
Usa la sustitución u para encontrar la antiderivada  ♦
♦
A veces necesitamos manipular una integral de formas que son más complicadas que simplemente multiplicar o dividir por una constante. Necesitamos eliminar todas las expresiones dentro del integrando que están en términos de la variable original. Cuando hayamos terminado, debería ser la única variable en el integrando. En algunos casos, esto significa resolver la variable original en términos de u. Esta técnica debería quedar clara en el siguiente ejemplo.
EJEMPLO ILUSTRATIVO 5.5_4. Encontrar una antiderivada usando la sustitución u
Usa la sustitución u para encontrar la antiderivada

Solución:
Si dejamos u = x − 1, entonces du = dx. Pero esto no tiene en cuenta la x en el numerador del integrando. Necesitamos expresar x en términos de u. Si u = x − 1, entonces x = u + 1. Ahora podemos reescribir la integral en términos de u:
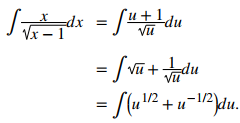
Luego integramos de la manera usual, reemplazamos u con la expresión original y factorizamos y simplificamos el resultado. Así que,
 ♦
♦
Ejercicio de control 5.5.4
Usa la sustitución u para encontrar la antiderivada 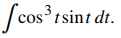 ♦
♦
Sustitución u con integrales definidas
La técnica de sustitución también se puede usar con integrales definidas. Sin embargo, usar la sustitución para evaluar una integral definida requiere un cambio en los límites de la integración. Si cambiamos las variables en el integrando, los límites de la integración también cambian.
TEOREMA 5.5.2. Sustitución u con integrales definidas
Sea \(u = g(x)\) y sea \(g’\) continua en un intervalo \([a, b]\), y sea \(f\) continua sobre el rango de \(u = g(x)\). Entonces,
\(\int_a^b f(g(x)) g'(x) dx = \int_{g(a)}^{g(b)} f(u) du.\)
♦
Aunque no probaremos formalmente este teorema, aquí lo justificamos con algunos cálculos. De la regla de sustitución para integrales indefinidas, si F(x) es una antiderivada de f (x), tenemos

Entonces

y tenemos el resultado deseado. ◊
EJEMPLO ILUSTRATIVO 5.5_5. Uso de sustitución u para evaluar una integral definida
Usar sustitución u para evaluar

Solución:
Sea u = 1 + 2x³, entonces du = 6x²dx. Como la función original incluye un factor de x² y du = 6x²dx, multiplique ambos lados de la ecuación du por 1/6. Entonces,

Para ajustar los límites de integración, tenga en cuenta que cuando x = 0, u = 1 + 2(0) = 1, y cuando x = 1, u = 1 + 2(1) = 3. Entonces

Al evaluar esta expresión, obtenemos
 ♦
♦
Ejercicio de control 5.5.5
Usa la sustitución para evaluar la integral definida \(\int_{-1}^{0} y(2y^2 – 3)^5 dy\). ♦
EJEMPLO ILUSTRATIVO 5.5_6. Usar sustitución u con una función exponencial
Usar sustitución u para evaluar

Solución:
Sea u = 4x² + 3. Entonces, du = 8xdx. Para ajustar los límites de integración, notamos que cuando x = 0, u = 3, y cuando x = 1, u = 7. Entonces nuestra sustitución da
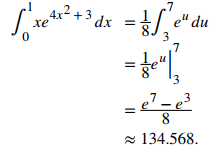
♦
Ejercicio de control 5.5.6
Usa la sustitución para evaluar \(\int_{0}^{1} x^2 \cos\left(\frac{\pi}{2}x^3\right) dx\). ♦
La sustitución puede ser solo una de las técnicas necesarias para evaluar una integral definida. Todas las propiedades y reglas de integración se aplican de forma independiente, y las funciones trigonométricas pueden necesitar reescribirse usando una identidad trigonométrica antes de que podamos aplicar la sustitución. Además, tenemos la opción de reemplazar la expresión original para u después de encontrar la antiderivada, lo que significa que no tenemos que cambiar los límites de integración. Estos dos enfoques se muestran en el siguiente ejemplo.
EJEMPLO ILUSTRATIVO 5.5_7. Usando la sustitución u para evaluar una integral trigonométrica
Usar sustitución u para evaluar

Solución:
Primero usemos una identidad trigonométrica para reescribir la integral. La identidad trigonométrica cos²θ = (1 + cos2θ)/2 nos permite reescribir la integral como

Entonces,

Podemos evaluar la primera integral tal como es, pero necesitamos hacer una sustitución para evaluar la segunda integral. Sea u = 2θ. Entonces, du = 2dθ, o du/2 = dθ. Además, cuando θ = 0, u = 0, y cuando θ = π/2, u = π. Expresando la segunda integral en términos de u, tenemos

♦

Pueden agregar más ejercicios
Puede ver mas ejercicios sobre sustitución “u” en mi canal de YouTube https://www.youtube.com/@JuanCarlosBeltranBeltran/search?query=Integraci%C3%B3n%20por%20sustituci%C3%B3n%20u