| Series de potencias | Ejercicios propuestos para el Capítulo 7.8 |

7.8 Propiedades de las series de potencias

Objetivos de aprendizaje:

7.8.1 Combina series de potencias mediante suma o resta.

7.8.2 Crea una nueva serie de potencias multiplicando por una potencia de la variable o una constante, o mediante una sustitución

7.8.3 Multiplica dos series de potencias.

7.8.4 Diferencia e integra series de potencias término por término.

En la sección anterior sobre series de potencias y funciones mostramos cómo representar ciertas funciones usando series de potencias. En esta sección discutimos cómo las series de potencias pueden combinarse, derivarse o integrarse para crear nuevas series de potencias. Esta capacidad es particularmente útil por un par de razones. Primero, nos permite encontrar representaciones en series de potencias para ciertas funciones elementales, al escribir esas funciones en términos de funciones con series de potencias conocidas. Por ejemplo, dada la representación en serie de potencias de \( f(x) = \frac{1}{1-x} \), podemos encontrar una representación en serie de potencias para \( f'(x) = \frac{1}{(1-x)^2} \). Segundo, la capacidad de crear series de potencias nos permite definir nuevas funciones que no pueden escribirse en términos de funciones elementales. Esta capacidad es particularmente útil para resolver ecuaciones diferenciales para las cuales no existe solución en términos de funciones elementales.

Combinando series de potencias

Si tenemos dos series de potencias con el mismo intervalo de convergencia, podemos sumar o restar las dos series para crear una nueva serie de potencias, también con el mismo intervalo de convergencia. De manera similar, podemos multiplicar una serie de potencias por una potencia de \(x\) o evaluar una serie de potencias en \(x^m\) para un entero positivo \(m\), creando así una nueva serie de potencias. Poder hacer esto nos permite encontrar representaciones en series de potencias para ciertas funciones utilizando representaciones en series de potencias de otras funciones. Por ejemplo, dado que conocemos la representación en serie de potencias para \(f(x) = \frac{1}{1-x}\), podemos encontrar representaciones en series de potencias para funciones relacionadas, como:

\(y = \frac{3x}{1-x^2}\) y \(y = \frac{1}{(x-1)(x-3)}.\)

En el siguiente teoremas “Combinación de Series de Potencias” se presentan resultados relacionados con la suma o resta de series de potencias, la composición de una serie de potencias, y la multiplicación de una serie de potencias por una potencia de la variable. Para simplicidad, enunciamos el teorema para series de potencias centradas en \(x = 0\). Resultados similares se aplican para series de potencias centradas en \(x = a\).

Teorema 7.8.1  Combinando Series de Potencias

Supongamos que las dos series de potencias \(\sum_{n=0}^\infty c_n x^n\) y \(\sum_{n=0}^\infty d_n x^n\) convergen a las funciones \(f\) y \(g\), respectivamente, en un intervalo común \(I\).

1. La serie de potencias \(\sum_{n=0}^\infty (c_n x^n \pm d_n x^n)\) converge a \(f \pm g\) en \(I\).
2. Para cualquier entero \(m \geq 0\) y cualquier número real \(b\), la serie de potencias \(\sum_{n=0}^\infty b x^m c_n x^n\) converge a \(b x^m f(x)\) en \(I\).
3. Para cualquier entero \(m \geq 0\) y cualquier número real \(b\), la serie \(\sum_{n=0}^\infty c_n (b x^m)^n\) converge a \(f(b x^m)\) para todos los \(x\) tales que \(b x^m\) está en \(I\). ♦

Prueba:

Probamos 1.: En el caso de la serie \(\sum_{n=0}^\infty (c_n x^n + d_n x^n)\). Supongamos que \(\sum_{n=0}^\infty c_n x^n\) y \(\sum_{n=0}^\infty d_n x^n\) convergen a las funciones \(f\) y \(g\), respectivamente, en el intervalo \(I\). Sea \(x\) un punto en \(I\) y sean \(S_N(x)\) y \(T_N(x)\) las sumas parciales de orden \(N\) de las series \(\sum_{n=0}^\infty c_n x^n\) y \(\sum_{n=0}^\infty d_n x^n\), respectivamente. Entonces, la secuencia \(\{S_N(x)\}\) converge a \(f(x)\) y la secuencia \(\{T_N(x)\}\) converge a \(g(x)\).

Además, la suma parcial de orden \(N\) de \(\sum_{n=0}^\infty (c_n x^n + d_n x^n)\) es:

\[ \sum_{n=0}^N (c_n x^n + d_n x^n) = \sum_{n=0}^N c_n x^n + \sum_{n=0}^N d_n x^n = S_N(x) + T_N(x). \]

Dado que:

\[ \lim_{N \to \infty} \big(S_N(x) + T_N(x)\big) = \lim_{N \to \infty} S_N(x) + \lim_{N \to \infty} T_N(x) = f(x) + g(x), \]

concluimos que la serie \(\sum_{n=0}^\infty (c_n x^n + d_n x^n)\) converge a \(f(x) + g(x)\). ♦

        Examinamos los productos de series de potencias en un teorema posterior. Primero, mostramos varias aplicaciones de la combinación de series de potencias y cómo encontrar el intervalo de convergencia de una serie de potencias dado el intervalo de convergencia de una serie de potencias relacionada.

Ejemplo ilustrativo 7.8.1  Combinando Series de Potencias

Suponga que \(\sum_{n=0}^{\infty}a_{n}x^{n}\) es una serie de potencias cuyo intervalo de convergencia es \((-1,1)\), y suponga que \(\sum_{n=0}^{\infty}b_{n}x^{n}\) es una serie de potencias cuyo intervalo de convergencia es \((-2,2)\). 1. Encuentre el intervalo de convergencia de la serie \[ \sum_{n=0}^{\infty} \left( \mathit{a}_n x^n + \mathit{b}_n x^n \right) \] 2. Encuentre el intervalo de convergencia de la serie \[ \sum_{n=0}^{\infty} \mathit{a}_n 3^n x^n \]

Solución:

1. Dado que el intervalo \((-1, 1)\) es un intervalo común de convergencia para las series \[ \sum_{n=0}^\infty \mathit{a}_n x^n \quad \text{y} \quad \sum_{n=0}^\infty \mathit{b}_n x^n, \] el intervalo de convergencia de la serie \[ \sum_{n=0}^\infty \left( \mathit{a}_n x^n + \mathit{b}_n x^n \right) \] es \((-1, 1)\). \[ \] 2. Dado que \(\sum_{n=0}^\infty \mathit{a}_n x^n\) es una serie de potencias centrada en cero con un radio de convergencia \(1\), converge para todos los valores de \(x\) en el intervalo \((-1, 1)\). Al combinar series de potencias, la serie \[ \sum_{n=0}^\infty \mathit{a}_n 3^n x^n = \sum_{n=0}^\infty \mathit{a}_n (3x)^n \] converge si \(3x\) está en el intervalo \((-1, 1)\). Por lo tanto, la serie converge para todos los valores de \(x\) en el intervalo \(\left(-\frac{1}{3}, \frac{1}{3}\right)\). ♦

Ejercicio de control 7.8.1

Suponga que \(\sum_{n=0}^\infty \mathit{a}_n x^n\) tiene un intervalo de convergencia de \((-1, 1)\). Encuentre el intervalo de convergencia de \(\sum_{n=0}^\infty \mathit{a}_n (x^2)^n\). ♦

En el siguiente ejemplo, mostramos cómo usar la combinación de series de potencias y la serie de potencias de una función \(f\) para construir series de potencias de funciones relacionadas con \(f\). Específicamente, consideramos funciones relacionadas con la función \(f(x) = \frac{1}{1 – x}\) y usamos el hecho de que: \[ \frac{1}{1 – x} = \sum_{n=0}^\infty x^n = 1 + x + x^2 + x^3 + \cdots, \quad \text{para } |x| < 1. \]

Ejemplo ilustrativo 7.8.2  Construcción de Series de Potencias a partir de Series de Potencias Conocidas

Use la representación en series de potencias para \(f(x) = \frac{1}{1 – x}\) junto con la técnica de combinar series de potencias para construir una serie de potencias para cada una de las siguientes funciones. Encuentre el intervalo de convergencia de la serie de potencias.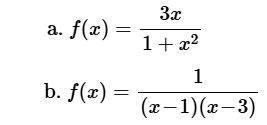

Solución:

a. Primero escribimos \(f(x)\) como: \[ f(x) = 3x \cdot \frac{1}{\left(1 – (-x^2)\right)}. \] Usando la representación en series de potencias para \(f(x) = \frac{1}{1 – x}\) y las partes (2) y (3) de la combinación de series de potencias, encontramos que una representación en series de potencias para \(f\) está dada por: \[ \sum_{n=0}^\infty 3x(-x^2)^n = \sum_{n=0}^\infty 3(-1)^n x^{2n+1}. \] Dado que el intervalo de convergencia de la serie para \(\frac{1}{1 – x}\) es \((-1, 1)\), el intervalo de convergencia para esta nueva serie es el conjunto de números reales \(x\) tales que \(|x^2| < 1\). Por lo tanto, el intervalo de convergencia es \((-1, 1)\). \[ \] b. Para encontrar la representación en series de potencias, usamos fracciones parciales para escribir \(f(x) = \frac{1}{(x - 1)(x - 3)}\) como la suma de dos fracciones. Tenemos: \[ \frac{1}{(x - 1)(x - 3)} = \frac{-1/2}{x - 1} + \frac{1/2}{x - 3} = \frac{1/2}{1 - x} - \frac{1/2}{3 - x} = \frac{1/2}{1 - x} - \frac{1/6}{1 - \frac{x}{3}}. \] Primero, usando la parte (2) de la combinación de series de potencias, obtenemos: \[ \frac{1}{2(1 - x)} = \sum_{n=0}^\infty \frac{1}{2}x^n, \quad \text{para } |x| < 1. \] Luego, usando las partes (2) y (3) de la combinación de series de potencias, tenemos: \[ \frac{1}{6\left(1 - \frac{x}{3}\right)} = \sum_{n=0}^\infty \frac{1}{6}\left(\frac{x}{3}\right)^n, \quad \text{para } |x| < 3. \] Dado que estamos combinando estas dos series de potencias, el intervalo de convergencia de la diferencia debe ser el menor de estos dos intervalos. Usando este hecho y la parte (1) de la combinación de series de potencias, tenemos: \[ \frac{1}{(x - 1)(x - 3)} = \sum_{n=0}^\infty \left(\frac{1}{2} - \frac{1}{6} \cdot 3^n\right)x^n, \] donde el intervalo de convergencia es \((-1, 1)\). ♦

Ejercicio de control 7.8.2

Use la serie para \(f(x) = \frac{1}{1 – x}\) en \(|x| < 1\) para construir una serie para \(\frac{1}{(1 - x)(x - 2)}\). Determine el intervalo de convergencia. ♦

En el Ejemplo 7.8.2, mostramos cómo encontrar series de potencias para ciertas funciones. En el Ejemplo 7.8.3 mostramos cómo hacer lo contrario: dada una serie de potencias, determinar qué función representa.

Ejemplo ilustrativo 7.8.3  Encontrar la Función Representada por una Serie de Potencias Dada

Considere la serie de potencias \(\sum_{n=0}^\infty 2^n x^n\). Encuentre la función \(f\) representada por esta serie. Determine el intervalo de convergencia de la serie.

Solución:

Escribiendo la serie dada como: \[ \sum_{n=0}^\infty 2^n x^n = \sum_{n=0}^\infty (2x)^n, \] podemos reconocer esta serie como la serie de potencias para: \[ f(x) = \frac{1}{1 – 2x}. \] Dado que esta es una serie geométrica, la serie converge si y solo si \(|2x| < 1\). Por lo tanto, el intervalo de convergencia es \((-1/2, 1/2)\). ♦

Ejercicio de control 7.8.3

Encuentre la función representada por la serie de potencias \(\sum_{n=0}^\infty \frac{1}{3^n} x^n\). Determine su intervalo de convergencia. ♦

      Recuerda las preguntas planteadas en la introducción del capítulo sobre cuál es la mejor manera de recibir los pagos de las ganancias de la lotería. Ahora revisitamos esas preguntas y mostramos cómo usar series para comparar el valor de los pagos a lo largo del tiempo con un pago único hoy. Calcularemos cuánto valen los pagos futuros en términos de los dólares de hoy, asumiendo que tenemos la capacidad de invertir las ganancias y ganar intereses. El valor de los pagos futuros en términos de los dólares de hoy se conoce como el valor presente de esos pagos.

Ejemplo ilustrativo 7.8.4  Introducción del Capítulo: Valor Presente de Ganancias Futuras

Supongamos que ganas la lotería y te dan las siguientes tres opciones: (1) Recibir 20 millones de dólares hoy; (2) recibir 1.5 millones de dólares por año durante los próximos 20 años; o (3) recibir 1 millón de dólares por año indefinidamente (pasando a tus herederos). ¿Cuál es la mejor opción, asumiendo que la tasa de interés anual es del 5%? Respondemos a esto trabajando con la siguiente secuencia de preguntas.

Solución:

Parte a: Valor Presente de un Pago Hecho al Final del Primer Año

Considera el pago de \( 1.5 \, \mathit{millones} \) de dólares hecho al final del primer año. Si pudieras recibir ese pago hoy en lugar de dentro de un año, podrías invertir ese dinero y ganar un interés del \( 5\% \). Por lo tanto, el valor presente de ese dinero \( P_1 \) satisface:

\[ P_1 (1 + 0.05) = 1.5 \, \mathit{millones} \] \[ P_1 = \frac{1.5}{1.05} = 1.429 \, \mathit{millones} \]

Parte b: Valor Presente de un Pago Hecho al Final del Segundo Año

De manera similar, considera el pago de \( 1.5 \, \mathit{millones} \) de dólares hecho al final del segundo año. Si pudieras recibir ese pago hoy, podrías invertir ese dinero durante dos años, ganando un \( 5\% \) de interés compuesto anualmente. Por lo tanto, el valor presente de ese dinero \( P_2 \) satisface:

\[ P_2 (1 + 0.05)^2 = 1.5 \, \mathit{millones} \] \[ P_2 = \frac{1.5}{(1.05)^2} = 1.361 \, \mathit{millones} \]

Parte c: Valor Presente de una Serie de Pagos Anuales Durante 20 Años

El valor presente de los pagos futuros hoy es la suma de los valores presentes \( P_1, P_2, \ldots, P_{20} \) de cada uno de esos pagos anuales. El valor presente de cada pago \( P_k \) se calcula de la siguiente manera:

\[ P_k = \frac{1.5}{(1.05)^k} \]

Por lo tanto, la suma total de los valores presentes es:

\[ P = \sum_{k=1}^{20} \frac{1.5}{(1.05)^k} = 18.693 \, \mathit{millones} \]

Parte d: Valor Presente de una Renta Vitalicia

Usando el resultado de la Parte a, podemos ver que el valor presente \( P \) de \( C \) dólares pagados anualmente durante \( n \) años, asumiendo una tasa de interés anual \( r \), se da por:

\[ P = C \left( \frac{1}{1+r} + \frac{C}{(1+r)^2} + \ldots + \frac{C}{(1+r)^n} \right) \]

Usando el resultado de la Parte b, vemos que el valor presente de una renta que continúa indefinidamente es dado por la siguiente serie infinita:

\[ P = \sum_{n=0}^{\infty} \frac{C}{(1+r)^{n+1}} \]

Podemos ver el valor presente como una serie de potencias en \( r \), que converge siempre y cuando \( |1 + r| < 1 \). Dado que \( r > 0 \), esta serie converge. Reescribiendo la serie, tenemos:

\[ P = C (1+r) \sum_{n=0}^{\infty} \left( \frac{1}{1+r} \right) ^n \]

Reconocemos que esta serie es la serie de potencias para:

\[ f(r) = \frac{1}{1-(1+r)} = \frac{1}{r(1+r)} \]

Por lo tanto, concluimos que el valor presente de esta renta vitalicia es:

\[ P = \frac{C}{r} \]

Parte e: Comparación Final

• Renta de 20 años: \( 18.693 \, \mathit{millones} \) de dólares
• Renta vitalicia: \( 20 \, \mathit{millones} \) de dólares

Por lo tanto, recibir un pago único de \( 20 \, \mathit{millones} \) de dólares hoy es equivalente, en valor presente, a recibir \( 1 \, \mathit{millón} \) de dólares por año indefinidamente o recibir \( 1.5 \, \mathit{millones} \) de dólares anualmente durante 20 años. ♦

Multiplicación de Series de Potencias

También podemos crear nuevas series de potencias multiplicando series de potencias. Poder multiplicar dos series de potencias proporciona otra forma de encontrar representaciones de funciones mediante series de potencias.

La forma en que multiplicamos series de potencias es similar a cómo multiplicamos polinomios. Por ejemplo, supongamos que queremos multiplicar:

\[ \sum_{n=0}^\infty c_n x^n = c_0 + c_1x + c_2x^2 + \cdots \] y \[ \sum_{n=0}^\infty d_n x^n = d_0 + d_1x + d_2x^2 + \cdots. \]

Parece que el producto debe satisfacer:

\[ \left( \sum_{n=0}^\infty c_n x^n \right) \left( \sum_{n=0}^\infty d_n x^n \right) = (c_0 + c_1x + c_2x^2 + \cdots) \cdot (d_0 + d_1x + d_2x^2 + \cdots). \]

Expandiendo, obtenemos:

\[ c_0 d_0 + (c_1 d_0 + c_0 d_1)x + (c_2 d_0 + c_1 d_1 + c_0 d_2)x^2 + \cdots. \]

En Multiplicación de Series de Potencias, establecemos el resultado principal sobre la multiplicación de series de potencias, mostrando que si:

\[ \sum_{n=0}^\infty c_n x^n \quad \text{y} \quad \sum_{n=0}^\infty d_n x^n \]

convergen en un intervalo común \( I \), entonces podemos multiplicar las series de esta manera, y la serie resultante también converge en el intervalo \( I \).

Teorema 7.8.2  Multiplicando Series de Potencias

Supongamos que las series de potencias:

\[ \sum_{n=0}^\infty c_n x^n \quad \text{y} \quad \sum_{n=0}^\infty d_n x^n \]

convergen a \( f \) y \( g \), respectivamente, en un intervalo común \( I \). Sea:

\[ e_n = c_0 d_n + c_1 d_{n-1} + c_2 d_{n-2} + \cdots + c_{n-1} d_1 + c_n d_0 = \sum_{k=0}^n c_k d_{n-k}. \]

Entonces:

\[ \left( \sum_{n=0}^\infty c_n x^n \right) \left( \sum_{n=0}^\infty d_n x^n \right) = \sum_{n=0}^\infty e_n x^n \]

y

\[ \sum_{n=0}^\infty e_n x^n \quad \text{converge a} \quad f(x) \cdot g(x) \quad \text{en} \quad I. \]

La serie:

\[ \sum_{n=0}^\infty e_n x^n \]

es conocida como el producto de Cauchy de las series:

\[ \sum_{n=0}^\infty c_n x^n \quad \text{y} \quad \sum_{n=0}^\infty d_n x^n. \] ♦

Omitimos la prueba de este teorema, ya que está más allá del nivel de este texto y se cubre típicamente en un curso más avanzado. Ahora proporcionamos un ejemplo de este teorema encontrando la representación en serie de potencias para

\[f(x) = \frac{1}{(1-x)(1-x^2)}\]

usando las representaciones en serie de potencias para

\[y = \frac{1}{1-x} \text{ y } y = \frac{1}{1-x^2}.\]

Ejemplo ilustrativo 7.8.5  Multiplicando Series de Potencias

Multiplica la representación en serie de potencias

\[\frac{1}{1-x} = \sum_{n=0}^{\infty} x^n = 1 + x + x^2 + x^3 + \cdots\]

para \(|x| < 1\) con la representación en serie de potencias

\[\frac{1}{1-x^2} = \sum_{n=0}^{\infty} (x^2)^n = 1 + x^2 + x^4 + x^6 + \cdots\]

para \(|x| < 1\) para construir una serie de potencias para

\[f(x) = \frac{1}{(1-x)(1-x^2)}\]

en el intervalo (-1, 1).

Solución:

Necesitamos multiplicar

\[(1 + x + x^2 + x^3 + \cdots)(1 + x^2 + x^4 + x^6 + \cdots).\]

Escribiendo los primeros términos, vemos que el producto está dado por

\[(1 + x^2 + x^4 + x^6 + \cdots) + (x + x^3 + x^5 + x^7 + \cdots) + (x^2 + x^4 + x^6 + x^8 + \cdots) + (x^3 + x^5 + x^7 + x^9 + \cdots)\]

= 1 + \( \mathit{x} \) + (1+1)\( \mathit{x}^2 \) + (1+1)\( \mathit{x}^3 \) + (1+1+1)\( \mathit{x}^4 \) + (1+1+1)\( \mathit{x}^5 \) + …

\[= 1 + x + 2x^2 + 2x^3 + 3x^4 + 3x^5 + \cdots.\]

♦

Dado que las series para \( y = \frac{1}{1 – \mathit{x}} \) y \( y = \frac{1}{1 – \mathit{x}^2} \) convergen en el intervalo \((-1, 1)\), la serie para el producto también converge en el intervalo \((-1, 1)\).

Ejercicio de control 7.8.4

Multiplica la serie \( \frac{1}{1 – \mathit{x}} = \sum_{n=0}^\infty \mathit{x}^n \) por sí misma para construir una serie para \( \frac{1}{(1 – \mathit{x})(1 – \mathit{x})} \). ♦

Diferenciando e Integrando Series de Potencias

Consideremos una serie de potencias

\[\sum_{n=0}^{\infty} c_n x^n = c_0 + c_1 x + c_2 x^2 + \cdots\]

que converge en algún intervalo I, y sea f la función definida por esta serie. Aquí abordamos dos preguntas sobre f.

• ¿Es \( f \) diferenciable? Y, de ser así, ¿cómo determinamos la derivada \( f’ \)?
• ¿Cómo evaluamos la integral indefinida \( \int f(\mathit{x}) \, dx \)?

Sabemos que, para un polinomio con un número finito de términos, podemos evaluar la derivada diferenciando cada término por separado. De manera similar, podemos evaluar la integral indefinida integrando cada término por separado. Aquí mostramos que podemos hacer lo mismo para las series de potencias convergentes. Es decir, si

\[f(x) = \sum_{n=0}^{\infty} c_n x^n = c_0 + c_1 x + c_2 x^2 + \cdots\]

converge en algún intervalo I, entonces

\[f'(x) = c_1 + 2c_2 x + 3c_3 x^2 + \cdots\]

y

\[\int f(x) \, dx = C + c_0 x + c_1 \frac{x^2}{2} + c_2 \frac{x^3}{3} + \cdots\]

converge en I. Como se indica a continuación, el comportamiento en los extremos del intervalo debe investigarse individualmente.

Evaluar la derivada y la integral indefinida de esta manera se llama diferenciación término a término de una serie de potencias y integración término a término de una serie de potencias, respectivamente. La capacidad de diferenciar e integrar series de potencias término a término también nos permite usar representaciones conocidas de series de potencias para encontrar representaciones de series de potencias para otras funciones. Por ejemplo, dada la serie de potencias para \(f(x) = \frac{1}{1-x}\), podemos diferenciar término a término para encontrar la serie de potencias para \(f'(x) = \frac{1}{(1-x)^2}\). De manera similar, utilizando la serie de potencias para

\[g(x) = \frac{1}{1+x}\]

podemos integrar término a término para encontrar la serie de potencias para \(G(x) = \ln(1+x)\), una antiderivada de \(g\). Mostramos cómo hacerlo en los ejemplos, Ejemplo 7.8.5 y Ejemplo 7.8.6, más adelante. Primero, enunciamos el teorema Diferenciación e Integración Término a Término para Series de Potencias, que proporciona el resultado principal respecto a la diferenciación e integración de series de potencias.

Teorema 7.8.2  Diferenciación e Integración Término a Término para Series de Potencias

Supongamos que la serie de potencias

\[\sum_{n=0}^{\infty}c_{n}(x-a)^{n}\]

converge en el intervalo \((a-R, a+R)\) para algún \(R > 0\). Sea f la función definida por la serie

\[f(x) = \sum_{n=0}^{\infty}c_{n}(x-a)^{n}\]

\[= c_{0} + c_{1}(x-a) + c_{2}(x-a)^{2} + c_{3}(x-a)^{3} + \cdots\]

para \(|x-a| < R\). Entonces f es diferenciable en el intervalo \((a-R, a+R)\) y podemos encontrar \(f^{\prime}\) diferenciando la serie término a término:

\[\begin{aligned} f^{\prime}(x) &= \sum_{n=1}^{\infty}nc_{n}(x-a)^{n-1} \\ &= c_{1} + 2c_{2}(x-a) + 3c_{3}(x-a)^{2} + \cdots \end{aligned}\]

para \(|x-a| < R\). Además, para encontrar \(\int f(x)dx\), podemos integrar la serie término a término. La serie resultante converge en \((a-R, a+R)\), y tenemos

\[\begin{aligned} \int f(x)dx &= C + \sum_{n=0}^{\infty}c_{n}\frac{(x-a)^{n+1}}{n+1} \\ &= C + c_{0}(x-a) + c_{1}\frac{(x-a)^{2}}{2} + c_{2}\frac{(x-a)^{3}}{3} + \cdots \end{aligned}\]

para \(|x-a| < R\). ♦

La demostración de este resultado está fuera del alcance del texto y se omite. Observa que, aunque la Diferenciación e Integración Término a Término para Series de Potencias garantiza el mismo radio de convergencia cuando una serie de potencias se diferencia o integra término a término, no dice nada sobre lo que sucede en los extremos. Es posible que las series de potencias diferenciadas e integradas tengan un comportamiento diferente en los extremos que la serie original. Vemos este comportamiento en los siguientes ejemplos.

Ejemplo ilustrativo 7.8.6  Diferenciando Series de Potencias

a. Use la representación en serie de potencias

\[f(x) = \frac{1}{1-x} = \sum_{n=0}^{\infty} x^n = 1 + x + x^2 + x^3 + \cdots\]

para \(|x| < 1\) para encontrar una representación en serie de potencias para

\[g(x) = \frac{1}{(1-x)^2}\]

en el intervalo \((-1,1)\). Determine si la serie resultante converge en los extremos.

b. Use el resultado de la parte a. para evaluar la suma de la serie

\[\sum_{n=0}^{\infty} \frac{n+1}{4^n}.\]

Solución:

a. Dado que

\[g(x)=\frac{1}{(1-x)^{2}}\]

es la derivada de

\[f(x) = \frac{1}{1-x},\]

podemos encontrar una representación en serie de potencias para g diferenciando la serie de potencias para f término a término. El resultado es

\[\begin{aligned} g(x)&=\frac{1}{(1-x)^{2}}\\ &=\frac{d}{dx}\left(\frac{1}{1-x}\right)\\ &=\sum_{n=0}^{\infty}\frac{d}{dx}(x^{n})\\ &=\frac{d}{dx}(1+x+x^{2}+x^{3}+\cdot\cdot\cdot)\\ &=0+1+2x+3x^{2}+4x^{3}+\cdot\cdot\cdot\\ &=\sum_{n=0}^{\infty}(n+1)x^{n} \end{aligned}\]

para \(|x|<1\). El Teorema de Diferenciación e Integración Término a Término para Series de Potencias no garantiza nada sobre el comportamiento de esta serie en los extremos. Probando los extremos usando el criterio de divergencia, encontramos que la serie diverge en ambos extremos \(x=\pm1\). Note que este es el mismo resultado encontrado en el Ejemplo 7.8.5.

b. De la parte a. sabemos que

\[\sum_{n=0}^{\infty}(n+1)x^{n}=\frac{1}{(1-x)^{2}}.\]

Por lo tanto,

\[\begin{aligned} \sum_{n=0}^{\infty}\frac{n+1}{4^{n}}&=\sum_{n=0}^{\infty}(n+1)\left(\frac{1}{4}\right)^{n}\\ &=\frac{1}{\left(1-\frac{1}{4}\right)^{2}}\\ &=\frac{1}{\left(\frac{3}{4}\right)^{2}}\\ &=\frac{16}{9} \end{aligned}\]

♦

Ejercicio de control 7.8.5

Diferencie la serie

\[\frac{1}{(1-x)^2} = \sum_{n=0}^{\infty} (n+1)x^n\]

término a término para encontrar una representación en serie de potencias para

\[\frac{2}{(1-x)^3}\]

en el intervalo \((-1,1)\). ♦

Ejemplo ilustrativo 7.8.7  Integrando Series de Potencias

Para cada una de las siguientes funciones f, encuentre una representación en serie de potencias para f integrando la serie de potencias para f’ y encuentre su intervalo de convergencia.

1. f (x) = ln(1 + x)

2. f (x) = tan^-1x

Solución:

a. Para \(f(x) = \ln(1+x)\), la derivada es \(f'(x) = \frac{1}{1+x}\). Sabemos que

\[\frac{1}{1+x} = \frac{1}{1-(-x)} = \sum_{n=0}^{\infty} (-x)^n = 1 – x + x^2 – x^3 + \cdots\]

para \(|x| < 1\). Para encontrar una serie de potencias para \(f(x) = \ln(1+x)\), integramos la serie término a término.

\[\begin{aligned} \int f'(x) dx &= \int (1 – x + x^2 – x^3 + \cdots) dx \\ &= C + x – \frac{x^2}{2} + \frac{x^3}{3} – \frac{x^4}{4} + \cdots \end{aligned}\]

Dado que \(f(0) = \ln(1+0) = 0\), tenemos \(C = 0\). Por lo tanto, la representación en serie de potencias para \(f(x) = \ln(1+x)\) es

\[\begin{aligned} \ln(1+x) &= x – \frac{x^2}{2} + \frac{x^3}{3} – \frac{x^4}{4} + \cdots \\ &= \sum_{n=1}^{\infty} (-1)^{n+1} \frac{x^n}{n} \end{aligned}\]

para \(|x| < 1\). El teorema de diferenciación e integración término a término no garantiza nada sobre el comportamiento de esta serie en los extremos. Sin embargo, al verificar los extremos, encontramos que en \(x = 1\) la serie es la serie armónica alternante, que converge. Además, en \(x = -1\), la serie es la serie armónica, que diverge. Es importante notar que, aunque la serie converge en \(x = 1\), el teorema de diferenciación e integración término a término no garantiza que la serie realmente converja a \(\ln(2)\). De hecho, la serie sí converge a \(\ln(2)\), pero demostrar este hecho requiere técnicas más avanzadas (el teorema de Abel, cubierto en textos más avanzados, trata este punto más técnico). El intervalo de convergencia es \((-1, 1]\).

b. La derivada de \(f(x) = \tan^{-1}x\) es \(f'(x) = \frac{1}{1+x^2}\). Sabemos que

\[\frac{1}{1+x^2} = \frac{1}{1-(-x^2)} = \sum_{n=0}^{\infty} (-x^2)^n = 1 – x^2 + x^4 – x^6 + \cdots\]

para \(|x| < 1\). Para encontrar una serie de potencias para \(f(x) = \tan^{-1}x\), integramos esta serie término a término.

\[\begin{aligned} \int f'(x) dx &= \int (1 – x^2 + x^4 – x^6 + \cdots) dx \\ &= C + x – \frac{x^3}{3} + \frac{x^5}{5} – \frac{x^7}{7} + \cdots \end{aligned}\]

Dado que \(\tan^{-1}(0) = 0\), tenemos \(C = 0\). Por lo tanto, una representación en serie de potencias para \(f(x) = \tan^{-1}x\) es

\[\begin{aligned} \tan^{-1}x &= x – \frac{x^3}{3} + \frac{x^5}{5} – \frac{x^7}{7} + \cdots \\ &= \sum_{n=0}^{\infty} (-1)^n \frac{x^{2n+1}}{2n+1} \end{aligned}\]

para \(|x| < 1\). Nuevamente, el teorema de diferenciación e integración término a término no garantiza nada sobre la convergencia de esta serie en los extremos. Sin embargo, al verificar los extremos y usar el criterio de la serie alternante, encontramos que la serie converge en \(x = 1\) y \(x = -1\). Como se discutió en la parte a., usando el teorema de Abel, se puede demostrar que la serie realmente converge a \(\tan^{-1}(1)\) y \(\tan^{-1}(-1)\) en \(x = 1\) y \(x = -1\), respectivamente. Por lo tanto, el intervalo de convergencia es \([-1, 1]\).

Ejercicio de control 7.8.6

Integre la serie de potencias \(\ln(1+x) = \sum_{n=1}^{\infty} (-1)^{n+1} \frac{x^n}{n}\) término a término para evaluar

\[\int \ln(1+x) \, dx.\] ♦

Hasta ahora, hemos mostrado varias técnicas para encontrar representaciones en series de potencias para funciones. Sin embargo, ¿cómo sabemos que estas series de potencias son únicas? Es decir, dada una función f y una serie de potencias para f en a, ¿es posible que exista una serie de potencias diferente para f en a que podríamos haber encontrado si hubiéramos usado una técnica diferente? La respuesta a esta pregunta es no. Este hecho no debería sorprendernos si pensamos en las series de potencias como polinomios con un número infinito de términos. Intuitivamente, si

\[c_0 + c_1x + c_2x^2 + \cdots = d_0 + d_1x + d_2x^2 + \cdots\]

para todos los valores x en algún intervalo abierto I alrededor de cero, entonces los coeficientes c_n deberían ser iguales a d_n para n ≥ 0. Ahora enunciamos este resultado formalmente en Unicidad de las Series de Potencias.

Teorema 7.8.2  Unicidad de las Series de Potencias

Sean \(\sum_{n=0}^{\infty} c_n(x – a)^n\) y \(\sum_{n=0}^{\infty} d_n(x – a)^n\) dos series de potencias convergentes tales que

\[\sum_{n=0}^{\infty} c_n(x – a)^n = \sum_{n=0}^{\infty} d_n(x – a)^n\]

para todo x en un intervalo abierto que contiene a a. Entonces \(c_n = d_n\) para todo \(n \geq 0\).♦

Demostración:

Sea

\[\begin{aligned} f(x) &= c_0 + c_1(x – a) + c_2(x – a)^2 + c_3(x – a)^3 + \cdots \\ &= d_0 + d_1(x – a) + d_2(x – a)^2 + d_3(x – a)^3 + \cdots. \end{aligned}\]

Entonces \(f(a) = c_0 = d_0\). Por el Teorema de Diferenciación e Integración Término a Término para Series de Potencias, podemos diferenciar ambas series término a término. Por lo tanto,

\[\begin{aligned} f'(x) &= c_1 + 2c_2(x – a) + 3c_3(x – a)^2 + \cdots \\ &= d_1 + 2d_2(x – a) + 3d_3(x – a)^2 + \cdots, \end{aligned}\]

y así, \(f'(a) = c_1 = d_1\). Similarmente,

\[\begin{aligned} f”(x) &= 2c_2 + 3\cdot2c_3(x – a) + \cdots \\ &= 2d_2 + 3\cdot2d_3(x – a) + \cdots \end{aligned}\]

implica que \(f”(a) = 2c_2 = 2d_2\), y por lo tanto, \(c_2 = d_2\). Más generalmente, para cualquier entero \(n \ge 0\), \(f^{(n)}(a) = n!c_n = n!d_n\) y consecuentemente \(c_n = d_n\) para todo \(n \ge 0\). ♦