| 1. Funciones y sus gráficas | 1.3 Funciones trigonométricas |
Ejercicios resueltos del capítulo 1.3
Strang 1.3_ 113 y 116 Convierta la medida de cada ángulo dado en grados a radianes. Escriba la respuesta como un múltiplo de π.
113. 240°
116. -225°
Strang 1.3_119 y 122 Para los siguientes ejercicios, convierta la medida de cada ángulo, dada en radianes, a grados.
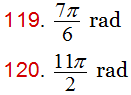
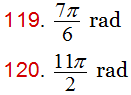
Strang 1.3_123 a 126 Calcule los siguientes valores funcionales:


Strang 1.3_129, 132 y 133
Considere el triángulo rectángulo ABC, rectángulo en C.
a) Encuentre la medida del lado del triángulo faltante.
b) Encuentre los valores de las seis funciones trigonométricas para A:
129. a = 4, c = 7
132. b = 40, c = 41
133. a = 84, b = 13


Strang 1.3_135 y 137
Para los siguientes ejercicios, P es un punto en el círculo unitario.
a) Halle el valor de coordenadas faltante (exacto) de cada punto.
b) Halle los valores de las seis funciones trigonométricas para el ángulo θ con un lado terminal que pasa por el punto P. Racionalice los denominadores.


Strang 1.3_139, 142, 144 y 146 Para los siguientes ejercicios, escriba cada expresión en términos de senos y cosenos, luego simplifique. La respuesta final no tiene que ser solo en términos de seno y coseno.


Strang 1.3_147, 150, 151, 153 y 154 Para los siguientes ejercicios, verifique que cada ecuación sea una identidad.


Strang 1.3_155, 157, 160 y 162 Para los siguientes ejercicios, resuelva las ecuaciones trigonométricas en el intervalo 0 ≤ θ < 2π.
155. 2senθ – 1 = 0
Solución – Juan Beltrán:


157. 2tan²θ = 2
Solución – Juan Beltrán:


160. 3secθ – 2√3 = 0
Solución – Juan Beltrán:


162. csc²θ + 2cscθ + 1 = 0
Solución – Juan Beltrán:


