Cuando creamos una matriz a partir de tres vectores, debemos tener cuidado con el orden en que enumeramos los vectores. Si los enumeramos en una matriz en un orden y luego reorganizamos las filas, el valor absoluto del determinante permanece sin cambios. Sin embargo, cada vez que dos filas cambian de lugar, el determinante cambia de signo:

Verificar este hecho es sencillo, pero bastante engorroso. Echemos un vistazo a esto con un ejemplo:
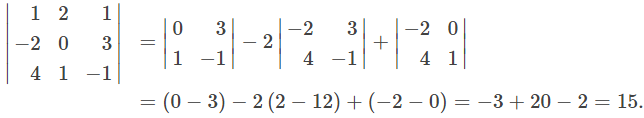
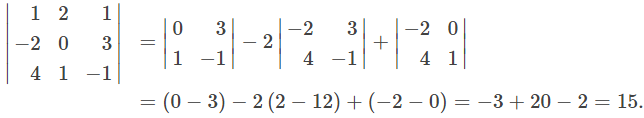
Cambiando las dos filas superiores obtenemos
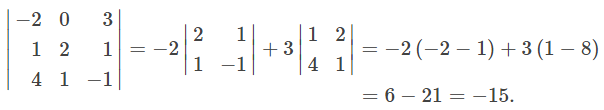
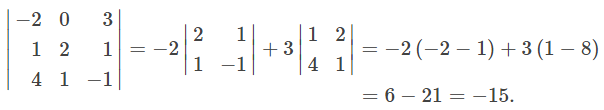
Reorganizar los vectores en los productos triples es equivalente a reordenar las filas en la matriz del determinante. Sea u = u = u₁i + u₂j + u₃k, v = v₁i + v₂j + v₃k, y w = w₁i + w₂j + w₃k. Aplicando el cálculo de un producto escalar triple, tenemos
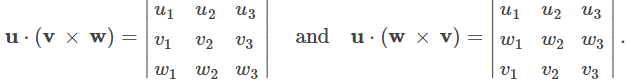
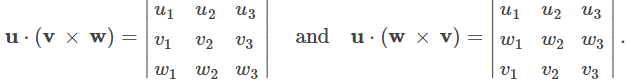
Podemos obtener el determinante para calcular u⋅ (w × v) cambiando las dos filas inferiores de u⋅ (v × w). Por lo tanto, u⋅ (v × w) = – u⋅ (w × v).
Siguiendo este razonamiento y explorando las diferentes formas en que podemos intercambiar variables en el producto triple escalar, se obtienen las siguientes identidades:
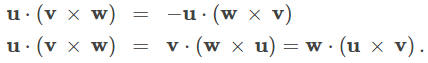
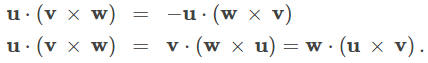
Sean u y v dos vectores en posición estándar. Si u y v no son múltiplos escalares entre sí, entonces estos vectores forman lados adyacentes de un paralelogramo. Vimos en el Área de un paralelogramo que el área de este paralelogramo es ∥u × v∥. Ahora supongamos que agregamos un tercer vector w que no se encuentra en el mismo plano que u y v pero que aún comparte el mismo punto inicial. Luego, estos vectores forman tres lados de un paralelepípedo, un prisma tridimensional con seis caras que son cada uno paralelogramos, como se muestra en la Figura 10.4_7. El volumen de este prisma es el producto de la altura y el área de su base. El producto escalar triple de u, v y w proporciona un método simple para calcular el volumen del paralelepípedo definido por estos vectores.
TEOREMA 10.4_5. Volumen de un paralelepípedoEl volumen de un paralelepípedo con bordes adyacentes dados por los vectores u, v, y w es el valor absoluto del producto escalar triple: V = | u⋅ (v × w) |. Ver figura 10.4_7 |
Tenga en cuenta que, como su nombre lo indica, el producto escalar triple produce un escalar. La fórmula de volumen que se acaba de presentar utiliza el valor absoluto de una cantidad escalar.
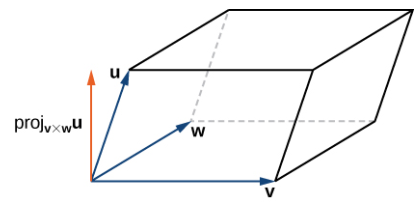

PruebaEl área de la base del paralelepípedo viene dada por ∥v × w∥. La altura de la figura viene dada por ∥projv × wu∥. El volumen del paralelepípedo es el producto de la altura y el área de la base, por lo que tenemos
|
EJEMPLO ILUSTRATIVO 10.4_11. Cálculo del volumen de un paralelepípedo
Sea u = ⟨− 1, −2, 1⟩, v = ⟨4, 3,2 ⟩ y w = ⟨0, −5, −2⟩. Encuentre el volumen del paralelepípedo con bordes adyacentes u, v y w (Figura 10.4_8).


Solución:
Tenemos


Por lo tanto, el volumen del paralelepípedo es | −40 | = 40 unidades³.
Aplicaciones del producto cruz
El producto cruza aparece en muchas aplicaciones prácticas en matemáticas, física e ingeniería. Examinemos algunas de estas aplicaciones aquí, incluida la idea del torque, con el que comenzamos esta sección. Otras aplicaciones aparecen en capítulos posteriores, particularmente en nuestro estudio de campos vectoriales como los campos gravitacionales y electromagnéticos (Introducción al cálculo vectorial).
EJEMPLO ILUSTRATIVO 10.4_12. Uso del producto escalar triple
Use el producto escalar triple para mostrar que los vectores u = ⟨2, 0, 5⟩, v = ⟨2, 2, 4⟩ y w = ⟨1, −1, 3⟩ son coplanares, es decir, demuestre que estos vectores se encuentran en el mismo plano.
Solución:
Comience calculando el producto escalar triple para encontrar el volumen del paralelepípedo definido por u, v, y w:
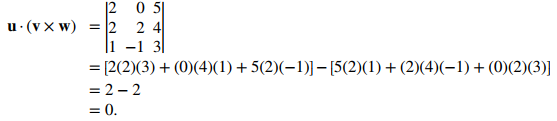
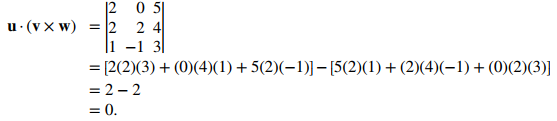
El volumen del paralelepípedo es de 0 unidades³, por lo que una de las dimensiones debe ser cero. Por lo tanto, los tres vectores se encuentran en el mismo plano.
EJEMPLO ILUSTRATIVO 10.4_13. Encontrar un vector ortogonal
Únicamente un solo plano puede pasar a través de cualquier conjunto de tres puntos no colineales. Encuentre un vector ortogonal al plano que contenga los puntos P = (9, −3, −2), Q = (1, 3, 0) y R = (- 2, 5, 0).
Solución:
El plano debe contener los vectores
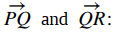
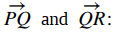
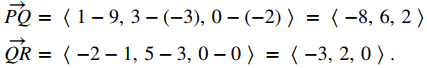
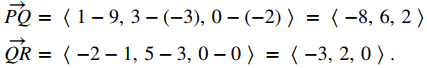
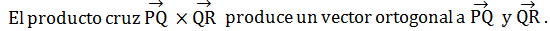
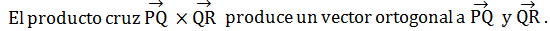
Por lo tanto, el producto cruz es ortogonal al plano que contiene estos dos vectores:
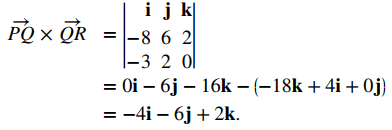
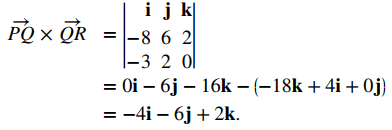
Hemos visto cómo usar el producto escalar triple y cómo encontrar un vector ortogonal a un plano. Ahora aplicamos el producto cruz a situaciones del mundo real.
Algunas veces una fuerza hace que un objeto gire. Por ejemplo, girar un destornillador o una llave crea este tipo de efecto de rotación, llamado torque.
DEFINICIÓN. TorqueTorque, τ (la letra griega tau), mide la tendencia de una fuerza a producir rotación alrededor de un eje de rotación. Sea r un vector con un punto inicial ubicado en el eje de rotación y con un punto terminal ubicado en el punto donde se aplica la fuerza, y deje que el vector F represente la fuerza. Entonces el torque es igual al producto cruzado de r y F: τ = r × F. Ver Figura 10.4_9. |
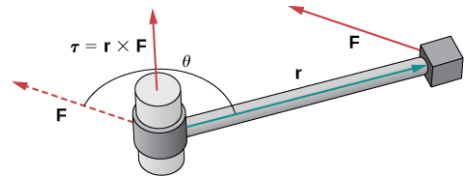

Piense en usar una llave para apretar un tornillo. El torque τ aplicado al perno depende de cuán fuerte empujemos la llave (fuerza) y cuán lejos del mango apliquemos la fuerza (distancia). El torque aumenta con una mayor fuerza sobre la llave a una mayor distancia del perno. Las unidades comunes de torque son el newton-metro o pie-libra. Aunque el torque es dimensionalmente equivalente al trabajo (tiene las mismas unidades), los dos conceptos son distintos. El torque se usa específicamente en el contexto de rotación, mientras que el trabajo generalmente implica movimiento a lo largo de una línea recta.
EJEMPLO ILUSTRATIVO 10.4_14. Evaluando el torque
Se aprieta un perno aplicando una fuerza de 6 N a una llave de 0,15 m (Figura 10.4_10). El ángulo entre la llave y el vector de fuerza es de 40°. Encuentre la magnitud del torque sobre el centro del perno. Redondea la respuesta a dos decimales.
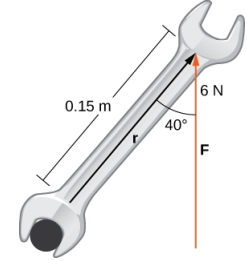

Solución:
Sustituya la información dada en la ecuación que define el torque:
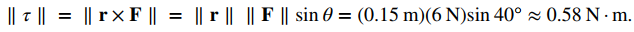
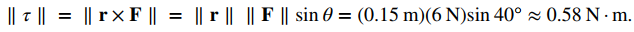

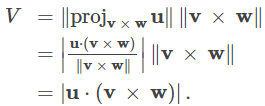
Hey there. I found your website via Google at the same time as searching for a related matter, your web site came up. It seems to be good. I have bookmarked it in my google bookmarks to visit then.
Great content! Super high-quality! Keep it up! 🙂