Hasta ahora en esta sección, nos hemos preocupado por la dirección del vector u × v, pero no hemos discutido su magnitud. Resulta que hay una expresión simple para la magnitud de u × v que involucra las magnitudes de u y v, y el seno del ángulo entre ellos.
TEOREMA 10.4_2. Magnitud del producto cruzSean u y v vectores, y sea θ el ángulo entre ellos. Entonces, ∥u × v∥ = ∥u∥⋅∥v∥⋅senθ. |
PruebaSean u = ⟨u₁, u₂, u₃⟩ y v = ⟨v₁, v₂, v₃⟩ vectores, y sea θ el ángulo entre ellos. Luego
Tomando raíces cuadradas y notando que
Nosotras tenemos el resultado deseado:
|
Esta definición del producto cruz nos permite visualizar o interpretar el producto geométricamente. Está claro, por ejemplo, que el producto cruz se define solo para vectores en tres dimensiones, no para vectores en dos dimensiones. En dos dimensiones, es imposible generar un vector simultáneamente ortogonal a dos vectores no paralelos.
EJEMPLO ILUSTRATIVO 10.4_5. Cálculo del producto cruz
Use las propiedades del producto cruzo para encontrar la magnitud del producto cruz de u = ⟨0,4,0⟩ y v = ⟨0,0, −3⟩.
Solución:
Tenemos
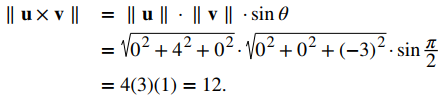
Determinantes y el producto cruz
Usar la ecuación dada en la definición del producto cruz para encontrar el producto cruz de dos vectores es sencillo y presenta el producto cruz en la forma de componente útil. La fórmula, sin embargo, es complicada y difícil de recordar. Afortunadamente, tenemos una alternativa. Podemos calcular el producto cruz de dos vectores usando notación de determinante.
♦ Un determinante 2 × 2 se define por
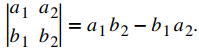
Por ejemplo

♦ El determinante 3 × 3 se define en términos de determinantes 2 × 2 de la siguiente manera:
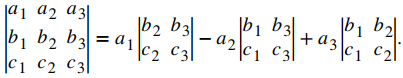
La ecuación anterior se conoce como la expansión del determinante a lo largo de la primera fila. Observe que los multiplicadores de cada uno de los determinantes 2 × 2 en el lado derecho de esta expresión son las entradas en la primera fila del determinante 3 × 3. Además, cada uno de los determinantes 2 × 2 contiene las entradas del determinante 3 × 3 que quedarían si tachara la fila y la columna que contiene el multiplicador. Por lo tanto, para el primer término a la derecha, a₁ es el multiplicador, y el determinante 2 × 2 contiene las entradas que quedan si tacha la primera fila y la primera columna del determinante 3 × 3. Del mismo modo, para el segundo término, el multiplicador es a₂, y el determinante 2 × 2 contiene las entradas que quedan si tacha la primera fila y la segunda columna del determinante 3 × 3. Observe, sin embargo, que el coeficiente del segundo término es negativo. El tercer término se puede calcular de manera similar.
EJEMPLO ILUSTRATIVO 10.4_6. Uso de la expansión a lo largo de la primera fila para calcular un determinante 3 × 3
Evaluar el determinante
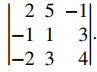
Tenemos
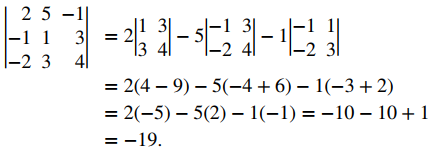
Técnicamente, los determinantes se definen sólo en términos de matrices de números reales. Sin embargo, la notación de determinante proporciona un dispositivo mnemónico útil para la fórmula del producto cruz.
REGLA: PRODUCTO CRUZ CALCULADO POR UN DETERMINANTESean u = ⟨u₁, u₂, u₃⟩ y v = ⟨v₁, v₂, v₃⟩ dos vectores. Entonces el producto cruz u × v viene dado por
|
EJEMPLO ILUSTRATIVO 10.4_7. Usando la notación de determinante para encontrar p × q
Sean p = ⟨− 1, 2, 5⟩ y q = ⟨4, 0, −3⟩. Encuentra p × q.
Solución:
Configuramos nuestro determinante colocando los vectores unitarios estándar en la primera fila, los componentes de u en la segunda fila y los componentes de v en la tercera fila. Entonces tenemos

Usando el producto cruz
El producto cruza es muy útil para varios tipos de cálculos, que incluyen encontrar un vector ortogonal a dos vectores dados, calcular áreas de triángulos y paralelogramos, e incluso determinar el volumen de la forma geométrica tridimensional hecha de paralelogramos conocidos como paralelepípedos.
EJEMPLO ILUSTRATIVO 10.4_8. Encontrar un vector unitario ortogonal a dos vectores dados
Sea a = ⟨5, 2, −1⟩ y b = ⟨0, −1, 4⟩. Encuentre un vector unitario ortogonal a a y b.
Solución:
El producto cruz a × b es ortogonal a ambos vectores a y b. Podemos calcularlo con un determinante:

Normalice este vector para encontrar un vector unitario en la misma dirección:
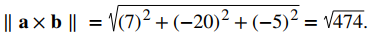
Así,

es un vector unitario ortogonal a a y b.
Para usar el producto cruz para calcular áreas, establecemos y probamos el siguiente teorema.
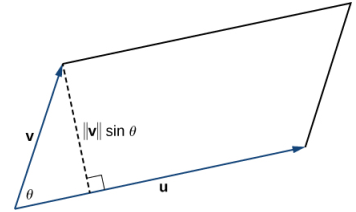
TEOREMA 10.4_3. Área de un paralelogramoSi ubicamos los vectores u y v de manera que formen lados adyacentes de un paralelogramo, entonces el área del paralelogramo viene dada por ∥u × v∥ (Figura 10.4_5). (Figura 10.4_5 El paralelogramo con lados adyacentes u y v tiene una base ∥u∥ y una altura ∥v∥senθ.) |
PruebaMostramos que la magnitud del producto cruz es igual a la base por la altura del paralelogramo.
|
EJEMPLO ILUSTRATIVO 10.4_9. Encontrar el área de un triángulo
Sean P = (1, 0, 0), Q = (0, 1, 0) y R = (0, 0, 1) los vértices de un triángulo (Figura 10.4_6). Encuentra su área.

Solución:
Tenemos
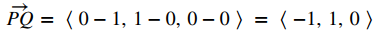
y
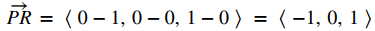
El área del paralelogramo con lados adyacentes
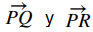
está dado por


El área de ΔPQR es la mitad del área del paralelogramo, o √3 / 2.
El producto escalar triple
Debido a que el producto cruz de dos vectores es un vector, es posible combinar el producto escalar y el producto cruz. El producto escalar de un vector con el producto cruz de otros dos vectores se llama producto escalar triple porque el resultado es un escalar.
DEFINICIÓN. Producto escalar tripleEl producto escalar triple de los vectores u, v y w es u⋅ (v × w). |
TEOREMA 10.4_4. Cálculo de un producto triple escalarEl producto escalar triple de los vectores u = u₁i + u₂j + u₃k, v = v₁i + v₂j + v₃k, y w = w₁i + w₂j + w₃k es el determinante de la matriz 3 × 3 formada por los componentes de los vectores:
|
PruebaEl cálculo es sencillo.
|
EJEMPLO ILUSTRATIVO 10.4_10. Cálculo del producto escalar triple
Sea u = ⟨1, 3, 5⟩, v = ⟨2, −1, 0⟩ y w = ⟨− 3, 0, −1⟩. Calcule el producto escalar triple u⋅ (v × w).
Solución:
Aplicar el cálculo de un producto escalar triple directamente:
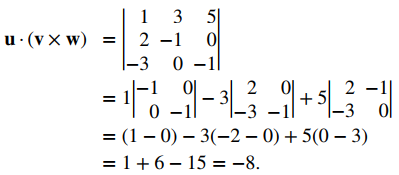


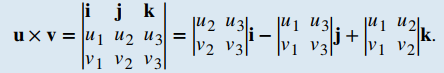
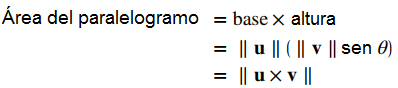
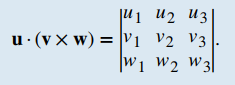
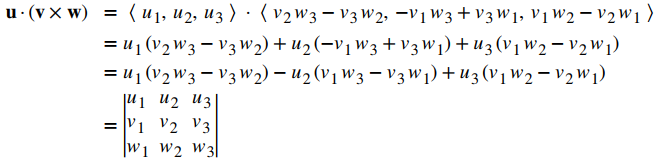
Hey there. I found your website via Google at the same time as searching for a related matter, your web site came up. It seems to be good. I have bookmarked it in my google bookmarks to visit then.
Great content! Super high-quality! Keep it up! 🙂