| 10. Cálculo vectorial – Vectores en el espacio | 10.4 El producto cruz |

Ejercicios propuestos para el Capítulo 10.4

Para los siguientes ejercicios, se dan los vectores $\mathbf{u}$ y $\mathbf{v}$.

1. Encuentre el producto vectorial $\mathbf{u} \times \mathbf{v}$ de los vectores $\mathbf{u}$ y $\mathbf{v}$. Exprese la respuesta en forma de componentes.
2. Esboce los vectores $\mathbf{u}$, $\mathbf{v}$ y $\mathbf{u} \times \mathbf{v}$.

183. $\mathbf{u} = \langle 2, 0, 0 \rangle, \mathbf{v} = \langle 2, 2, 0 \rangle$
184. $\mathbf{u} = \langle 3, 2, -1 \rangle, \mathbf{v} = \langle 1, 1, 0 \rangle$
185. $\mathbf{u} = 2\mathbf{i} + 3\mathbf{j}, \mathbf{v} = \mathbf{j} + 2\mathbf{k}$
186. $\mathbf{u} = 2\mathbf{j} + 3\mathbf{k}, \mathbf{v} = 3\mathbf{i} + \mathbf{k}$

187. Simplifique $(\mathbf{i} \times \mathbf{i} – 2\mathbf{i} \times \mathbf{j} – 4\mathbf{i} \times \mathbf{k} + 3\mathbf{j} \times \mathbf{k}) \times \mathbf{i}$.
188. Simplifique $\mathbf{j} \times (\mathbf{k} \times \mathbf{j} + 2\mathbf{j} \times \mathbf{i} – 3\mathbf{j} \times \mathbf{j} + 5\mathbf{i} \times \mathbf{k})$.

En los siguientes ejercicios, se dan los vectores $\mathbf{u}$ y $\mathbf{v}$. Encuentre un vector unitario $\mathbf{w}$ en la dirección del vector producto vectorial $\mathbf{u} \times \mathbf{v}$. Exprese su respuesta usando vectores unitarios estándar.

189. $\mathbf{u} = \langle 3, -1, 2 \rangle, \mathbf{v} = \langle -2, 0, 1 \rangle$
190. $\mathbf{u} = \langle 2, 6, 1 \rangle, \mathbf{v} = \langle 3, 0, 1 \rangle$
191. $\mathbf{u} = \overrightarrow{AB}, \mathbf{v} = \overrightarrow{AC}$, donde $A(1, 0, 1), B(1, -1, 3)$ y $C(0, 0, 5)$
192. $\mathbf{u} = \overrightarrow{OP}, \mathbf{v} = \overrightarrow{PQ}$, donde $P(-1, 1, 0)$ y $Q(0, 2, 1)$

193. Determine el número real $\alpha$ tal que $\mathbf{u} \times \mathbf{v}$ e $\mathbf{i}$ sean ortogonales, donde $\mathbf{u} = 3\mathbf{i} + \mathbf{j} – 5\mathbf{k}$ y $\mathbf{v} = 4\mathbf{i} – 2\mathbf{j} + \alpha\mathbf{k}$.

194. Demuestre que $\mathbf{u} \times \mathbf{v}$ y $2\mathbf{i} – 14\mathbf{j} + 2\mathbf{k}$ no pueden ser ortogonales para cualquier número real $\alpha$, donde $\mathbf{u} = \mathbf{i} + 7\mathbf{j} – \mathbf{k}$ y $\mathbf{v} = \alpha\mathbf{i} + 5\mathbf{j} + \mathbf{k}$.

195. Demuestre que $\mathbf{u} \times \mathbf{v}$ es ortogonal a $\mathbf{u} + \mathbf{v}$ y a $\mathbf{u} – \mathbf{v}$, donde $\mathbf{u}$ y $\mathbf{v}$ son vectores no nulos.

196. Demuestre que $\mathbf{v} \times \mathbf{u}$ es ortogonal a $(\mathbf{u} \cdot \mathbf{v})(\mathbf{u} + \mathbf{v}) + \mathbf{u}$, donde $\mathbf{u}$ y $\mathbf{v}$ son vectores no nulos.

197. Calcule el determinante $\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & -1 & 7 \\ 2 & 0 & 3 \end{vmatrix}$.

198. Calcule el determinante $\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & 3 & -4 \\ 1 & 6 & -1 \end{vmatrix}$.

Para los siguientes ejercicios, se dan los vectores $\mathbf{u}$ y $\mathbf{v}$. Use la notación de determinante para encontrar el vector $\mathbf{w}$ ortogonal a los vectores $\mathbf{u}$ y $\mathbf{v}$.

199. $\mathbf{u} = \langle -1, 0, e^t \rangle, \mathbf{v} = \langle 1, e^{-t}, 0 \rangle$, donde $t$ es un número real.
200. $\mathbf{u} = \langle 1, 0, x \rangle, \mathbf{v} = \langle \frac{2}{x}, 1, 0 \rangle$, donde $x$ es un número real distinto de cero.

201. Encuentre el vector $(\mathbf{a} – 2\mathbf{b}) \times \mathbf{c}$, donde $\mathbf{a} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 2 & -1 & 5 \\ 0 & 1 & 8 \end{vmatrix}$, $\mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & 1 & 1 \\ 2 & -1 & -2 \end{vmatrix}$, y $\mathbf{c} = \mathbf{i} + \mathbf{j} + \mathbf{k}$.

202. Encuentre el vector $\mathbf{c} \times (\mathbf{a} + 3\mathbf{b})$, donde $\mathbf{a} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 5 & 0 & 9 \\ 0 & 1 & 0 \end{vmatrix}$, $\mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & -1 & 1 \\ 7 & 1 & -1 \end{vmatrix}$, y $\mathbf{c} = \mathbf{i} – \mathbf{k}$.

203. [T] Use el producto vectorial $\mathbf{u} \times \mathbf{v}$ para encontrar el ángulo agudo entre los vectores $\mathbf{u}$ y $\mathbf{v}$, donde $\mathbf{u} = \mathbf{i} + 2\mathbf{j}$ y $\mathbf{v} = \mathbf{i} + \mathbf{k}$. Exprese la respuesta en grados redondeados al entero más cercano.

204. [T] Use el producto vectorial $\mathbf{u} \times \mathbf{v}$ para encontrar el ángulo obtuso entre los vectores $\mathbf{u}$ y $\mathbf{v}$, donde $\mathbf{u} = -\mathbf{i} + 3\mathbf{j} + \mathbf{k}$ y $\mathbf{v} = \mathbf{i} – 2\mathbf{j}$. Exprese la respuesta en grados redondeados al entero más cercano.

205. Use el seno y el coseno del ángulo entre dos vectores no nulos $\mathbf{u}$ y $\mathbf{v}$ para demostrar la identidad de Lagrange: $\|\mathbf{u} \times \mathbf{v}\|^2 = \|\mathbf{u}\|^2 \|\mathbf{v}\|^2 – (\mathbf{u} \cdot \mathbf{v})^2$.

206. Verifique la identidad de Lagrange $\|\mathbf{u} \times \mathbf{v}\|^2 = \|\mathbf{u}\|^2 \|\mathbf{v}\|^2 – (\mathbf{u} \cdot \mathbf{v})^2$ para los vectores $\mathbf{u} = -\mathbf{i} + \mathbf{j} – 2\mathbf{k}$ y $\mathbf{v} = 2\mathbf{i} – \mathbf{j}$.

207. Dos vectores no nulos $\mathbf{u}$ y $\mathbf{v}$ se llaman colineales si existe un escalar no nulo $\alpha$ tal que $\mathbf{v} = \alpha\mathbf{u}$. Demuestre que $\mathbf{u}$ y $\mathbf{v}$ son colineales si y solo si $\mathbf{u} \times \mathbf{v} = \mathbf{0}$.

208. Dos vectores no nulos $\mathbf{u}$ y $\mathbf{v}$ se llaman colineales si existe un escalar no nulo $\alpha$ tal que $\mathbf{v} = \alpha\mathbf{u}$. Demuestre que los vectores $\overrightarrow{AB}$ y $\overrightarrow{AC}$ son colineales, donde $A(4, 1, 0), B(6, 5, -2)$ y $C(5, 3, -1)$.

209. Encuentre el área del paralelogramo con lados adyacentes $\mathbf{u} = \langle 3, 2, 0 \rangle$ y $\mathbf{v} = \langle 0, 2, 1 \rangle$.

210. Encuentre el área del paralelogramo con lados adyacentes $\mathbf{u} = \mathbf{i} + \mathbf{j}$ y $\mathbf{v} = \mathbf{i} + \mathbf{k}$.

211. Considere los puntos $A(3, -1, 2)$, $B(2, 1, 5)$ y $C(1, -2, -2)$.

1. Encuentre el área del paralelogramo $ABCD$ con lados adyacentes $\overrightarrow{AB}$ y $\overrightarrow{AC}$.
2. Encuentre el área del triángulo $ABC$.
3. Encuentre la distancia desde el punto $A$ a la línea $BC$.

212. Considere los puntos $A(2, -3, 4)$, $B(0, 1, 2)$ y $C(-1, 2, 0)$.

1. Encuentre el área del paralelogramo $ABCD$ con lados adyacentes $\overrightarrow{AB}$ y $\overrightarrow{AC}$.
2. Encuentre el área del triángulo $ABC$.
3. Encuentre la distancia desde el punto $B$ a la línea $AC$.

En los siguientes ejercicios, se dan los vectores $\mathbf{u}$, $\mathbf{v}$ y $\mathbf{w}$.

1. Encuentre el triple producto escalar $\mathbf{u} \cdot (\mathbf{v} \times \mathbf{w})$.
2. Encuentre el volumen del paralelepípedo con las aristas adyacentes $\mathbf{u}$, $\mathbf{v}$ y $\mathbf{w}$.

213. $\mathbf{u} = \mathbf{i} + \mathbf{j}, \mathbf{v} = \mathbf{j} + \mathbf{k}, \text{ y } \mathbf{w} = \mathbf{i} + \mathbf{k}$
214. $\mathbf{u} = \langle -3, 5, -1 \rangle, \mathbf{v} = \langle 0, 2, -2 \rangle, \text{ y } \mathbf{w} = \langle 3, 1, 1 \rangle$

215. Calcule los triples productos escalares $\mathbf{v} \cdot (\mathbf{u} \times \mathbf{w})$ y $\mathbf{w} \cdot (\mathbf{u} \times \mathbf{v})$, donde $\mathbf{u} = \langle 1, 1, 1 \rangle$, $\mathbf{v} = \langle 7, 6, 9 \rangle$ y $\mathbf{w} = \langle 4, 2, 7 \rangle$.

216. Calcule los triples productos escalares $\mathbf{w} \cdot (\mathbf{v} \times \mathbf{u})$ y $\mathbf{u} \cdot (\mathbf{w} \times \mathbf{v})$, donde $\mathbf{u} = \langle 4, 2, -1 \rangle$, $\mathbf{v} = \langle 2, 5, -3 \rangle$ y $\mathbf{w} = \langle 9, 5, -10 \rangle$.

217. Encuentre los vectores $\mathbf{a}$, $\mathbf{b}$ y $\mathbf{c}$ con un triple producto escalar dado por el determinante $\begin{vmatrix} 1 & 2 & 3 \\ 0 & 2 & 5 \\ 8 & 9 & 2 \end{vmatrix}$. Determine su triple producto escalar.

218. El triple producto escalar de los vectores $\mathbf{a}$, $\mathbf{b}$ y $\mathbf{c}$ está dado por el determinante $\begin{vmatrix} 0 & -2 & 1 \\ 0 & 1 & 4 \\ 1 & -3 & 7 \end{vmatrix}$. Encuentre el vector $\mathbf{a} – \mathbf{b} + \mathbf{c}$.

219. Considere el paralelepípedo con aristas $OA, OB$ y $OC$, donde $A(2, 1, 0)$, $B(1, 2, 0)$ y $C(0, 1, \alpha)$.

1. Encuentre el número real $\alpha > 0$ tal que el volumen del paralelepípedo sea $3 \text{ unidades}^3$.
2. Para $\alpha = 1$, encuentre la altura $h$ desde el vértice $C$ del paralelepípedo al plano formado por las aristas $OA$ y $OB$.

220. Considere los puntos $A(\alpha, 0, 0)$, $B(0, \beta, 0)$ y $C(0, 0, \gamma)$, con $\alpha, \beta$ y $\gamma$ números reales positivos.

1. Determine el volumen del paralelepípedo con lados adyacentes $\overrightarrow{OA}, \overrightarrow{OB}$ y $\overrightarrow{OC}$.
2. Encuentre el volumen del tetraedro con vértices $O, A, B$ y $C$. (Sugerencia: El volumen del tetraedro es $1/6$ del volumen del paralelepípedo).
3. Encuentre la distancia desde el origen al plano determinado por $A, B$ y $C$. Esboce el paralelepípedo y el tetraedro.

221. Sean $\mathbf{u}, \mathbf{v}$ y $\mathbf{w}$ vectores tridimensionales y $c$ un número real. Demuestre las siguientes propiedades del producto vectorial.

1. $\mathbf{u} \times \mathbf{u} = \mathbf{0}$
2. $\mathbf{u} \times (\mathbf{v} + \mathbf{w}) = (\mathbf{u} \times \mathbf{v}) + (\mathbf{u} \times \mathbf{w})$
3. $c(\mathbf{u} \times \mathbf{v}) = (c\mathbf{u}) \times \mathbf{v} = \mathbf{u} \times (c\mathbf{v})$
4. $\mathbf{u} \cdot (\mathbf{u} \times \mathbf{v}) = 0$

222. Demuestre que los vectores $\mathbf{u} = \langle 1, 0, -8 \rangle$, $\mathbf{v} = \langle 0, 1, 6 \rangle$ y $\mathbf{w} = \langle -1, 9, 3 \rangle$ satisfacen las siguientes propiedades del producto vectorial.

1. $\mathbf{u} \times \mathbf{u} = \mathbf{0}$
2. $\mathbf{u} \times (\mathbf{v} + \mathbf{w}) = (\mathbf{u} \times \mathbf{v}) + (\mathbf{u} \times \mathbf{w})$
3. $c(\mathbf{u} \times \mathbf{v}) = (c\mathbf{u}) \times \mathbf{v} = \mathbf{u} \times (c\mathbf{v})$
4. $\mathbf{u} \cdot (\mathbf{u} \times \mathbf{v}) = 0$

223. Se dice que los vectores no nulos $\mathbf{u}$, $\mathbf{v}$ y $\mathbf{w}$ son linealmente dependientes si uno de los vectores es una combinación lineal de los otros dos. Por ejemplo, existen dos números reales no nulos $\alpha$ y $\beta$ tales que $\mathbf{w} = \alpha\mathbf{u} + \beta\mathbf{v}$. De lo contrario, los vectores se llaman linealmente independientes. Demuestre que $\mathbf{u}$, $\mathbf{v}$ y $\mathbf{w}$ son coplanares si y solo si son linealmente dependientes.

224. Considere los vectores $\mathbf{u} = \langle 1, 4, -7 \rangle$, $\mathbf{v} = \langle 2, -1, 4 \rangle$, $\mathbf{w} = \langle 0, -9, 18 \rangle$ y $\mathbf{p} = \langle 0, -9, 17 \rangle$.

1. Demuestre que $\mathbf{u}$, $\mathbf{v}$ y $\mathbf{w}$ son coplanares usando su triple producto escalar.
2. Demuestre que $\mathbf{u}$, $\mathbf{v}$ y $\mathbf{w}$ son coplanares usando la definición de que existen dos números reales no nulos $\alpha$ y $\beta$ tales que $\mathbf{w} = \alpha\mathbf{u} + \beta\mathbf{v}$.
3. Demuestre que $\mathbf{u}$, $\mathbf{v}$ y $\mathbf{p}$ son linealmente independientes; es decir, ninguno de los vectores es una combinación lineal de los otros dos.

225. Considere los puntos $A(0, 0, 2)$, $B(1, 0, 2)$, $C(1, 1, 2)$ y $D(0, 1, 2)$. ¿Son los vectores $\overrightarrow{AB}$, $\overrightarrow{AC}$ y $\overrightarrow{AD}$ linealmente dependientes (es decir, uno de los vectores es una combinación lineal de los otros dos)?

226. Demuestre que los vectores $\mathbf{i} + \mathbf{j}$, $\mathbf{i} – \mathbf{j}$ e $\mathbf{i} + \mathbf{j} + \mathbf{k}$ son linealmente independientes; es decir, no existen dos números reales no nulos $\alpha$ y $\beta$ tales que $\mathbf{i} + \mathbf{j} + \mathbf{k} = \alpha(\mathbf{i} + \mathbf{j}) + \beta(\mathbf{i} – \mathbf{j})$.

227. Sean $\mathbf{u} = \langle u_1, u_2 \rangle$ y $\mathbf{v} = \langle v_1, v_2 \rangle$ vectores bidimensionales. El producto vectorial de los vectores $\mathbf{u}$ y $\mathbf{v}$ no está definido. Sin embargo, si los vectores se consideran como los vectores tridimensionales $\mathbf{\tilde{u}} = \langle u_1, u_2, 0 \rangle$ y $\mathbf{\tilde{v}} = \langle v_1, v_2, 0 \rangle$, respectivamente, entonces, en este caso, podemos definir el producto vectorial de $\mathbf{\tilde{u}}$ y $\mathbf{\tilde{v}}$. En particular, en notación de determinante, el producto vectorial de $\mathbf{\tilde{u}}$ y $\mathbf{\tilde{v}}$ está dado por

$\mathbf{\tilde{u}} \times \mathbf{\tilde{v}} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ u_1 & u_2 & 0 \\ v_1 & v_2 & 0 \end{vmatrix}$.

Use este resultado para calcular $(\mathbf{i} \cos \theta + \mathbf{j} \sin \theta) \times (\mathbf{i} \sin \theta – \mathbf{j} \cos \theta)$, donde $\theta$ es un número real.

228. Considere los puntos $P(2, 1)$, $Q(4, 2)$ y $R(1, 2)$.

1. Encuentre el área del triángulo $P, Q$ y $R$.
2. Determine la distancia desde el punto $R$ a la recta que pasa por $P$ y $Q$.

229. Determine un vector de magnitud $10$ perpendicular al plano que pasa por el eje $x$ y el punto $P(1, 2, 4)$.

230. Determine un vector unitario perpendicular al plano que pasa por el eje $z$ y el punto $A(3, 1, -2)$.

231. Considere $\mathbf{u}$ y $\mathbf{v}$ dos vectores tridimensionales. Si la magnitud del vector producto vectorial $\mathbf{u} \times \mathbf{v}$ es $k$ veces mayor que la magnitud del vector $\mathbf{u}$, demuestre que la magnitud de $\mathbf{v}$ es mayor o igual a $k$, donde $k$ es un número natural.

232. [T] Suponga que se conocen las magnitudes de dos vectores no nulos $\mathbf{u}$ y $\mathbf{v}$. La función $f(\theta) = \|\mathbf{u}\| \|\mathbf{v}\| \sin \theta$ define la magnitud del vector producto vectorial $\mathbf{u} \times \mathbf{v}$, donde $\theta \in [0, \pi]$ es el ángulo entre $\mathbf{u}$ y $\mathbf{v}$.

1. Grafique la función $f$.
2. Encuentre el mínimo y máximo absolutos de la función $f$. Interprete los resultados.
3. Si $\|\mathbf{u}\| = 5$ y $\|\mathbf{v}\| = 2$, encuentre el ángulo entre $\mathbf{u}$ y $\mathbf{v}$ si la magnitud de su vector producto vectorial es igual a $9$.

233. Encuentre todos los vectores $\mathbf{w} = \langle w_1, w_2, w_3 \rangle$ que satisfacen la ecuación $\langle 1, 1, 1 \rangle \times \mathbf{w} = \langle -1, -1, 2 \rangle$.

234. Resuelva la ecuación $\mathbf{w} \times \langle 1, 0, -1 \rangle = \langle 3, 0, 3 \rangle$, donde $\mathbf{w} = \langle w_1, w_2, w_3 \rangle$ es un vector no nulo con una magnitud de $3$.

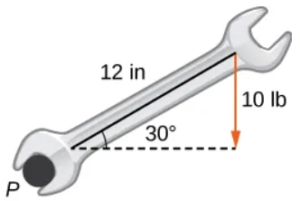
235. [T] Un mecánico usa una llave de $12\text{ pulgadas}$ para girar un perno. La llave forma un ángulo de $30^\circ$ con la horizontal. Si el mecánico aplica una fuerza vertical de $10\text{ lb}$ en el mango de la llave, ¿cuál es la magnitud del torque en el punto $P$? Exprese la respuesta en pies-libras redondeada a dos decimales.

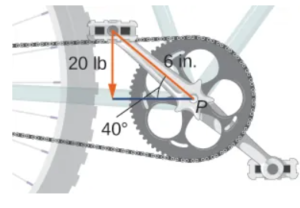
236. [T] Un niño aplica los frenos en una bicicleta aplicando una fuerza descendente de $20 \text{ lb}$ en el pedal cuando la biela de $6 \text{ pulgadas}$ forma un ángulo de $40^\circ$ con la horizontal. Encuentre el torque en el punto $P$. Exprese su respuesta en pies-libras redondeada a dos decimales.

237. [T] Encuentre la magnitud de la fuerza que debe aplicarse al extremo de una llave de $20\text{ cm}$ situada en la dirección positiva del eje $y$, si la fuerza se aplica en la dirección $\langle 0, 1, -2 \rangle$ y produce un torque de $100\text{ N} \cdot \text{m}$ al perno situado en el origen.

238. [T] ¿Cuál es la magnitud de la fuerza que debe aplicarse al extremo de una llave de $1\text{ ft}$ con un ángulo de $35^\circ$ para producir un torque de $20\text{ N} \cdot \text{m}$?

239. [T] El vector de fuerza $\mathbf{F}$ que actúa sobre un protón con una carga eléctrica de $1.6 \times 10^{-19}\text{ C}$ (en culombios) que se mueve en un campo magnético $\mathbf{B}$ donde el vector de velocidad $\mathbf{v}$ viene dado por $\mathbf{F} = 1.6 \times 10^{-19}(\mathbf{v} \times \mathbf{B})$ (aquí, $\mathbf{v}$ se expresa en metros por segundo, $\mathbf{B}$ está en teslas [T] y $\mathbf{F}$ está en newtons [N]). Encuentre la fuerza que actúa sobre un protón que se mueve en el plano $xy$ con una velocidad $\mathbf{v} = 10^5\mathbf{i} + 10^5\mathbf{j}$ (en metros por segundo) en un campo magnético dado por $\mathbf{B} = 0.3\mathbf{j}$.

240. [T] El vector de fuerza $\mathbf{F}$ que actúa sobre un protón con una carga eléctrica de $1.6 \times 10^{-19}\text{ C}$ que se mueve en un campo magnético $\mathbf{B}$ donde el vector de velocidad $\mathbf{v}$ viene dado por $\mathbf{F} = 1.6 \times 10^{-19}(\mathbf{v} \times \mathbf{B})$ (aquí, $\mathbf{v}$ se expresa en metros por segundo, $\mathbf{B}$ en T y $\mathbf{F}$ en N). Si la magnitud de la fuerza $\mathbf{F}$ que actúa sobre un protón es $5.9 \times 10^{-17}\text{ N}$ y el protón se mueve a una velocidad de $300\text{ m/seg}$ en un campo magnético $\mathbf{B}$ de magnitud $2.4\text{ T}$, encuentre el ángulo entre el vector de velocidad $\mathbf{v}$ del protón y el campo magnético $\mathbf{B}$. Exprese la respuesta en grados redondeados al entero más cercano.

241. [T] Considere $\mathbf{r}(t) = \langle \cos t, \sin t, 2t \rangle$ el vector de posición de una partícula en el tiempo $t \in [0, 30]$, donde las componentes de $\mathbf{r}$ se expresan en centímetros y el tiempo en segundos. Sea $\overrightarrow{OP}$ el vector de posición de la partícula después de $1\text{ seg}$.

1. Determine el vector unitario $\mathbf{B}(t)$ (llamado vector unitario binormal) que tiene la dirección del vector producto vectorial $\mathbf{v}(t) \times \mathbf{a}(t)$, donde $\mathbf{v}(t)$ y $\mathbf{a}(t)$ son el vector de velocidad instantánea y el vector de aceleración de la partícula después de $t$ segundos, respectivamente.
2. Use un CAS para visualizar los vectores $\mathbf{v}(1), \mathbf{a}(1)$ y $\mathbf{B}(1)$ como vectores que parten del punto $P$ junto con la trayectoria de la partícula.

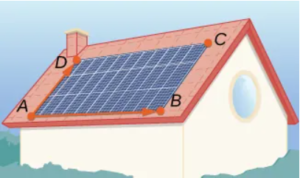
242. Un panel solar está montado en el techo de una casa. El panel puede considerarse posicionado en los puntos con coordenadas (en metros) $A(8, 0, 0)$, $B(8, 18, 0)$, $C(0, 18, 8)$ y $D(0, 0, 8)$.

1. Encuentre el vector $\mathbf{n} = \overrightarrow{AB} \times \overrightarrow{AD}$ perpendicular a la superficie de los paneles solares. Exprese la respuesta usando vectores unitarios estándar.
2. Suponga que el vector unitario $\mathbf{s} = \frac{1}{\sqrt{3}}\mathbf{i} + \frac{1}{\sqrt{3}}\mathbf{j} + \frac{1}{\sqrt{3}}\mathbf{k}$ apunta hacia el Sol en un momento particular del día y el flujo de energía solar es $\mathbf{F} = 900\mathbf{s}$ (en vatios por metro cuadrado $[\text{W/m}^2]$). Encuentre la cantidad predicha de potencia eléctrica que el panel puede producir, la cual está dada por el producto punto de los vectores $\mathbf{F}$ y $\mathbf{n}$ (expresada en vatios).
3. Determine el ángulo de elevación del Sol sobre el panel solar. Exprese la respuesta en grados redondeados al número entero más cercano. (Sugerencia: El ángulo entre los vectores $\mathbf{n}$ y $\mathbf{s}$ y el ángulo de elevación son complementarios).