| 9. Ecuaciones diferenciales | 9.5 Ecuaciones lineales de segundo orden | 9.5.1 Ecuaciones lineales homogéneas |
Ejercicios propuestos para el Capítulo 9.5.1
1. (a) Verifique que y1 = e2x y y2 = e5x son soluciones de
y″ − 7y′ + 10y = 0 (A)
en (−∞, ∞).
(b) Verifique que si c1 y c2 son constantes arbitrarias, entonces y = c1e2x + c2e5x es una solución de (A) en (−∞, ∞).
(c) Resuelva el problema de valor inicial
y″ − 7y′ + 10y = 0, y(0) = −1, y′(0) = 1.
(d) Resuelva el problema de valor inicial
y″ − 7y′ + 10y = 0, y(0) = k0, y′(0) = k1.
2. (a) Verifique que y1 = excosx e y2 = exsenx son soluciones de
y″ − 2y′ + 2y = 0 (A)
en (−∞, ∞).
(b) Verifique que si c1 y c2 son constantes arbitrarias, entonces y = c1ex cosx + c2ex senx es una solución de (A) en (−∞, ∞).
(c) Resuelva el problema de valor inicial
y″ − 2y′ + 2y = 0, y(0) = 3, y′(0) = −2.
(d) Resuelva el problema de valor inicial
y″ − 2y′ + 2y = 0, y(0) = k0, y′(0) = k1.
3. (a) Verifique que y1 = ex y y2 = xex son soluciones de
y″ − 2y′ + y = 0 (A)
en (−∞, ∞).
(b) Verifique que si c1 y c2 son constantes arbitrarias, entonces y = ex(c1 + c2x) es una solución de (A) en (−∞, ∞).
(c) Resuelva el problema de valor inicial
y″ − 2y′ + y = 0, y(0) = 7, y′(0) = 4.
(d) Resuelva el problema de valor inicial
y″ − 2y′ + y = 0, y(0) = k0, y′(0) = k1.
4. (a) Verifique que y1 = 1/(x − 1) y y2 = 1/(x + 1) son soluciones de
(x2 − 1)y″ + 4xy′ + 2y = 0 (A)
en (−∞, −1), (−1, 1) y (1, ∞). ¿Cuál es la solución general de (A) en cada uno de estos intervalos?
(b) Resuelva el problema de valor inicial
(x2 − 1)y″ + 4xy′ + 2y = 0, y(0) = −5, y′(0) = 1.
¿Cuál es el intervalo de validez de la solución?
(c) C/G Representa gráficamente la solución del problema de valor inicial.
(d) Verifique la fórmula de Abel para y1 y y2, con x0 = 0.
5. Calcule los Wronskianos de los conjuntos de funciones dados


6. Encuentre el Wronskiano de un conjunto dado {y1, y2} de soluciones de
y″ + 3(x2 + 1)y′ − 2y = 0,
dado que W(π) = 0
7. Encuentre el Wronskiano de un conjunto dado {y1, y2} de soluciones de
(1 − x2)y″ − 2xy′ + α(α + 1)y = 0,
dado que W(0) = 1. (Esta es la ecuación de Legendre).
8. Encuentre el Wronskiano de un conjunto dado {y1, y2} de soluciones de
x2y″ + xy′ + (x2 − ν2)y = 0,
dado que W(1) = 1. (Esta es la ecuación de Bessel.)
9. (Este ejercicio muestra que si conoce una solución no trivial de y″ + p(x)y′ + q(x)y = 0, usted
puede usar la fórmula de Abel para encontrar otra).
Suponga que p y q son continuas y y1 es una solución de
y″ + p(x)y′ + q(x)y = 0 (A)
que no tiene ceros en (a, b). Sea P(x) = ∫p(x)dx cualquier antiderivada de p sobre (a, b).
(a) Demuestre que si K es una constante arbitraria distinta de cero y y2 satisface
y1y2′ − y1′y2 = Ke−P(x) (B)
en (a, b), entonces y2 también satisface (A) en (a, b), y {y1, y2} es un conjunto fundamental de soluciones de (A) en (a, b).
(b) Concluya de (a) que si y2 = uy1 donde 

En los ejercicios 10 a 23, use el método sugerido en el ejercicio 9 para encontrar una segunda solución y2 que no sea un múltiplo constante de la solución y1. Elija K convenientemente para simplificar y2.
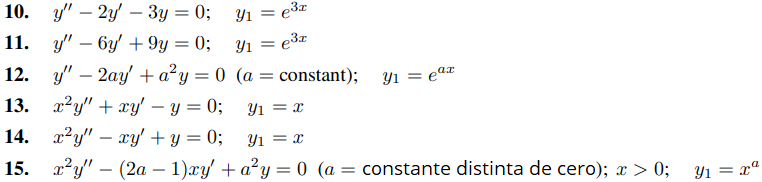
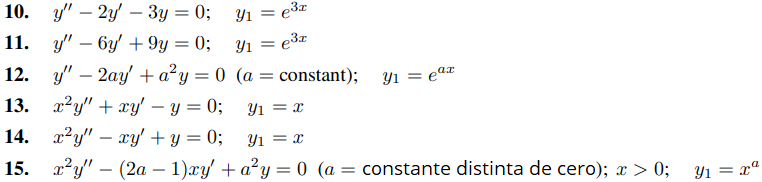
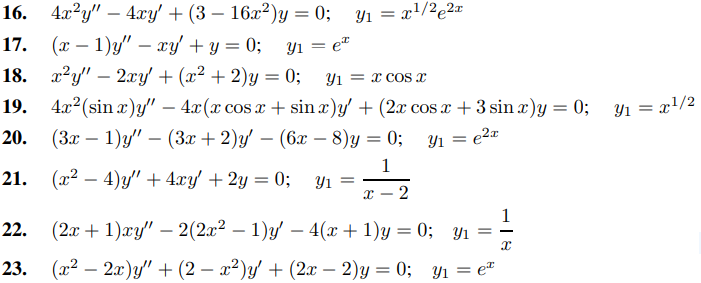
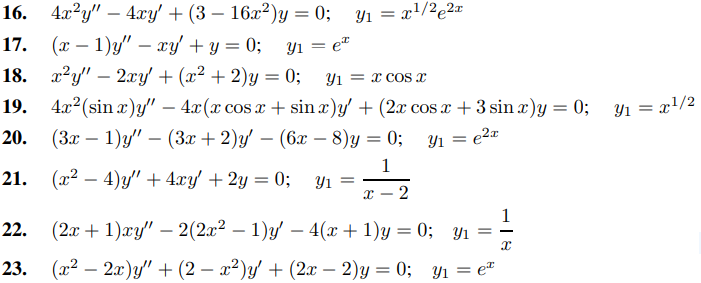
24. Suponga que p y q son continuas en un intervalo abierto (a, b) y sea x0 en (a, b). Utilice el teorema 9.5.1.1 para demostrar que la única solución del problema de valor inicial
y″ + p(x)y′ + q(x)y = 0, y(x0) = 0, y′(x0) = 0
en (a, b) es la solución trivial y ≡ 0.
25. Suponga que P0, P1 y P2 son continuas en (a, b) y sea x0 en (a, b). Demuestre que si alguna de las siguientes afirmaciones es verdadera, entonces P0(x) = 0 para alguna x en (a, b).
(a) El problema del valor inicial
P0(x)y″ + P1(x)y′ + P2(x)y = 0, y(x0) = k0, y′(x0) = k1
tiene más de una solución en (a, b).
(b) El problema del valor inicial
P0(x)y″ + P1(x)y′ + P2(x)y = 0, y(x0) = 0, y′(x0) = 0
tiene una solución no trivial en (a, b).
26. Suponga que p y q son continuas en (a, b) y y1 e y2 son soluciones de
y″ + p(x)y′ + q(x)y = 0 (A)
en (a, b). Sea
z1 = αy1 + βy2 y z2 = γy1 + δy2,
donde α, β, γ y δ son constantes. Muestre que si {z1, z2} es un conjunto fundamental de soluciones de (A) sobre (a, b), entonces también lo es {y1, y2}.
27. Suponga que p y q son continuas en (a, b) y {y1, y2} es un conjunto fundamental de soluciones de
y″ + p(x)y′ + q(x)y = 0 (A)
donde α, β, γ y δ son constantes. Muestre que si {z1, z2} es un conjunto fundamental de soluciones de (A) sobre (a, b) si y solo si αγ − βδ ≠ 0.
28. Suponga que y1 es diferenciable en un intervalo (a, b) y y2 = ky1, donde k es una constante. Muestre que el Wronskiano de {y1, y2} es idénticamente cero en (a, b).
29. Sea


(a) Demuestre que el Wronskiano de {y1, y2} está definido y es idénticamente cero en (−∞, ∞).
(b) Suponga que a < 0 < b. Muestre que {y1, y2} es linealmente independiente en (a, b).
(c) Use el ejercicio 25(b) para demostrar que estos resultados no contradicen el teorema 9.5.1.5, porque ni y1 ni y2 pueden ser una solución de una ecuación
y″ + p(x)y′ + q(x)y = 0
en (a, b) si p y q son continuas en (a, b).
30. Suponga que p y q son continuas en (a, b) y {y1, y2} es un conjunto de soluciones de
y″ + p(x)y′ + q(x)y = 0
en (a, b) tal que y1(x0) = y2(x0) = 0 o y1′ (x0) = y2′ (x0) = 0 para algún x0 en (a, b). Demuestre que {y1, y2} depende linealmente de (a, b).
31. Suponga que p y q son continuas en (a, b) y {y1, y2} es un conjunto fundamental de soluciones de
y″ + p(x)y′ + q(x)y = 0
en (a, b). Demuestre que si y1(x1) = y1(x2) = 0, donde a < x1 < x2) < b, entonces y2(x) = 0 para alguna x en (x1, x2). AYUDA: Demuestre que si y2 no tiene ceros en (x1, x2), entonces y1/y2 es estrictamente creciente o estrictamente decreciente en (x1, x2) y deduzca una contradicción.
32. Suponga que p y q son continuas en (a, b) y toda solución de
y″ + p(x)y′ + q(x)y = 0 (A)
en (a, b) se puede escribir como una combinación lineal de las funciones diferenciables dos veces {y1, y2}. Utilice el teorema 9.5.1.1 para demostrar que y1 e y2 son soluciones de (A) en (a, b).
33. Suponga que p1, p2, q1 y q2 son continuas en (a, b) y las ecuaciones
y″ + p1(x)y′ + q1(x)y = 0 y y″ + p2(x)y′ + q2(x)y = 0
tienen las mismas soluciones en (a, b). Demuestre que p1 = p2 y q1 = q2 en (a, b). PISTA: Usa la fórmula de Abel.
34. (Para este ejercicio, debe conocer los determinantes de 3×3). Demuestre que si y1 y y2 son dos veces continuamente diferenciables en (a, b) y el Wronskiano W de {y1, y2} no tiene ceros en (a, b) entonces la ecuación
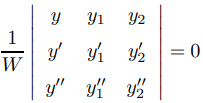
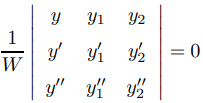
Se puede escribir como
y″ + p(x)y′ + q(x)y = 0 (A)
donde p y q son continuas en (a, b) y {y1, y2} es un conjunto fundamental de soluciones de (A) en (a, b). AYUDA: Expanda el determinante por cofactores de su primera columna.
35. Use el método sugerido por el ejercicio 34 para encontrar una ecuación lineal homogénea para la cual las funciones dadas formen un conjunto fundamental de soluciones en algún intervalo.


36. Suponga que p y q son continuas en (a, b) y {y1, y2} es un conjunto fundamental de soluciones de
y″ + p(x)y′ + q(x)y = 0 (A)
en (a, b). Demuestre que si y es una solución de (A) en (a, b), hay exactamente una forma de elegir c1 y c2 de modo que y = c1y1 + c2y2 en (a, b).
37. Supongamos que p y q son continuas en (a, b) y x0 está en (a, b). Sean y1 e y2 las soluciones de
y″ + p(x)y′ + q(x)y = 0 (A)
tal que
y1(x0) = 1, y1′ (x0) = 0 y y2(x0) = 0, y2′ (x0) = 1.
(El teorema 9.5.1.1 implica que cada uno de estos problemas de valor inicial tiene una solución única en (a, b).)
(a) Demuestre que {y1, y2} es linealmente independiente en (a, b).
(b) Demuestre que una solución arbitraria y de (A) en (a, b) se puede escribir como y = y(x0)y1 + y0(x0)y2.
(c) Exprese la solución del problema de valor inicial
y″ + p(x)y′ + q(x)y = 0, y(x0) = k0, y′(x0) = k1
como una combinación lineal de y1 e y2.
38. Encuentre soluciones y1 e y2 de la ecuación y″ = 0 que satisfagan las condiciones iniciales
y1(x0) = 1, y1′(x0) = 0 y y2(x0) = 0, y2′ (x0) = 1
Luego use el Ejercicio 37 (c) para escribir la solución del problema de valor inicial
y″ = 0, y(0) = k0, y′(0) = k1
como una combinación lineal de y1 e y2.
39. Sea x0 un número real arbitrario. Dado (Ejemplo 9.5.1.1) que ex y e−x son soluciones de y″ − y =0, encuentre las soluciones y1 y y2 de y″ − y = 0 tales que
y1(x0) = 1, y1′ (x0) = 0 y y2(x0) = 0, y2′ (x0) = 1.
Luego use el Ejercicio 37 (c) para escribir la solución del problema de valor inicial
y″ − y = 0, y(x0) = k0, y′(x0) = k1
como una combinación lineal de y1 e y2.
40. Sea x0 un número real arbitrario. Dado (Ejemplo 9.5.1.2) que cosωx y senωx son soluciones de y″+ ω2y = 0, encuentre soluciones de y″ + ω2y = 0 tales que
y1(x0) = 1, y1′ (x0) = 0 y y2(x0) = 0, y2′ (x0) = 1.
Luego use el Ejercicio 37 (c) para escribir la solución del problema de valor inicial
y″ + ω2y = 0, y(x0) = k0, y′(x0) = k1
como una combinación lineal de y1 e y2. Use las identidades
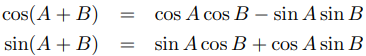
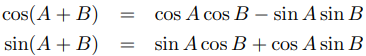
para simplificar sus expresiones para y1, y2 e y.
41. Recuerda del Ejercicio 4 que 1/(x − 1) y 1/(x + 1) son soluciones de
(x2 − 1)y″ + 4xy′ + 2y = 0 (A)
en (−1, 1). Encuentre soluciones de (A) tales que
y1(0) = 1, y1′ (0) = 0 y y2(0) = 0, y2′ (0) = 1.
Luego use el Ejercicio 37 (c) para escribir la solución del problema de valor inicial
(x2 − 1)y″ + 4xy′ + 2y = 0, y(0) = k0, y′(0) = k1
como una combinación lineal de y1 e y2.
42. (a) Verifique que y1 = x2 y y2 = x3 satisfacen
x2y″ − 4xy′ + 6y = 0 (A)
en (−∞, ∞) y que {y1, y2} es un conjunto fundamental de soluciones de (A) en (−∞, 0) y (0, ∞).
(b) Sean las constantes a1, a2, b1 y b2. Muestre que
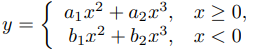
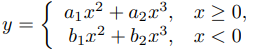
es una solución de (A) en (−∞, ∞) si y solo si a1 = b1. A partir de esto, justifica el enunciado de que y es una solución de (A) en (−∞, ∞) si y solo si
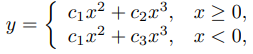
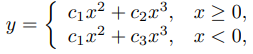
donde c1, c2 y c3 son constantes arbitrarias.
(c) ¿Para qué valores de k0 y k1 el problema de valor inicial


tiene una solución? ¿Cuáles son las soluciones?
(d) Demuestre que si x0 ≠ 0 y k0, k1 son constantes arbitrarias, el problema de valor inicial
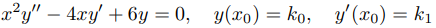
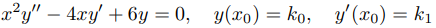
tiene infinitas soluciones en (−∞, ∞). ¿En qué intervalo (B) tiene solución única?
43. (a) Verifique que y1 = x y y2 = x2 satisfacen
x2y″ − 2xy′ + 2y = 0 (A)
en (−∞, ∞) y que {y1, y2} es un conjunto fundamental de soluciones de (A) en (−∞, 0) y (0, ∞).
(b) Sean las constantes a1, a2, b1 y b2. demuestre que


es una solución de (A) en (−∞, ∞) si y solo si a1 = b1 y a2 = b2. A partir de esto, justifique el enunciado de que la solución general de (A) en (−∞, ∞) es y = c1x + c2x2, donde c1 y c2 son constantes arbitrarias.
(c) ¿Para qué valores de k0 y k1 el problema de valor inicial


tiene una solución? ¿Cuáles son las soluciones?
(d) Demuestre que si x0 ≠ 0 y k0, k1 son constantes arbitrarias, entonces el problema de valor inicial
x2y″ − 2xy′ + 2y = 0, y(x0) = k0, y′(x0) = k1
tiene solución única en (−∞, ∞).
44. (a) Verifique que y1 = x3 y y2 = x4 satisfacen
x2y″ − 6xy′ + 12y = 0 (A)
en (−∞, ∞), y que {y1, y2} es un conjunto fundamental de soluciones de (A) en (−∞, 0) y (0, ∞).
(b) Demuestre que y es una solución de (A) en (−∞, ∞) si y solo si


donde a1, a2, b1 y b2 son constantes arbitrarias.
(c) ¿Para qué valores de k0 y k1 el problema de valor inicial
x2y″ − 6xy′ + 12y = 0, y(0) = k0, y′(0) = k1
tiene una solución? ¿Cuáles son las soluciones?
(d) Demuestre que si x0 ≠ 0 y k0, k1 son constantes arbitrarias, entonces el problema de valor inicial
x2y″ − 6xy′ + 12y = 0, y(x0) = k0, y′(x0) = k1 (B)
tiene infinitas soluciones en (−∞, ∞). ¿En qué intervalo (B) tiene solución única?
