Ecuaciones para un plano
Sabemos que una recta está determinada por dos puntos. En otras palabras, para dos puntos distintos, hay exactamente una recta que pasa a través de esos puntos, ya sea en dos dimensiones o en tres. Del mismo modo, dados tres puntos que no todos se encuentran en la misma recta, hay un plano único que pasa por estos puntos. Así como una recta está determinada por dos puntos, un plano está determinado por tres.
Esta puede ser la forma más sencilla de caracterizar un plano, pero también podemos usar otras descripciones. Por ejemplo, dadas dos rectas distintas que se intersecan, hay exactamente un plano que contiene ambas rectas. Un plano también está determinado por una recta y cualquier punto que no se encuentre en la recta. Estas caracterizaciones surgen naturalmente de la idea de que un plano está determinado por tres puntos. Quizás la caracterización más sorprendente de un plano es en realidad la más útil.
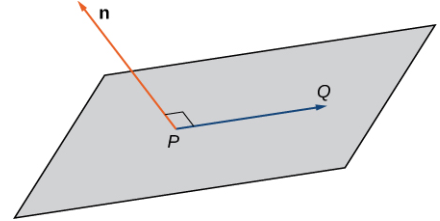
Imagine un par de vectores ortogonales que comparten un punto inicial. Visualice agarrando uno de los vectores y girándolo. A medida que gira, el otro vector gira y barre un plano. Aquí, describimos ese concepto matemáticamente. Sea n = ⟨a, b, c⟩ un vector y P = (x0, y0, z0) un punto. Entonces el conjunto de todos los puntos Q = (x, y, z) tal que el vector PQ es ortogonal a n forma un plano (figura 10.5_6). Decimos que n es un vector normal, o perpendicular al plano. Recuerde, el producto escalar de los vectores ortogonales es cero. Este hecho genera la ecuación vectorial de un plano: n⋅PQ = 0. Reescribir esta ecuación proporciona formas adicionales de describir el plano:
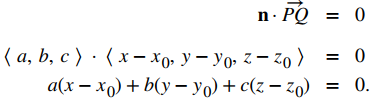
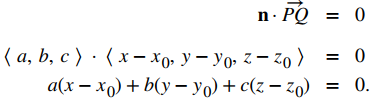
DEFINICIÓN. Ecuación de un plano
Definición. Ecuación de un planoDado un punto P y un vector n, el conjunto de todos los puntos Q que satisfacen la ecuación
forma un plano La ecuación
se conoce como la ecuación vectorial de un plano. La ecuación escalar de un plano que contiene el punto P = (x0, y0, z0) con el vector normal n = ⟨a, b, c⟩ es
Esta ecuación se puede expresar como ax + by + cz + d = 0, donde d = −ax0 − by0 − cz0. Esta forma de la ecuación a veces se llama la forma general de la ecuación de un plano. |
Como se describió anteriormente en esta sección, los tres puntos que no están todos en la misma recta determinan un plano. Dados tres de estos puntos, podemos encontrar una ecuación para el plano que contiene estos puntos.
EJEMPLO ILUSTRATIVO 10.5_5. Escribir una ecuación de un plano dados tres puntos en el plano
Escriba una ecuación para el plano que contiene los puntos P = (1, 1, −2), Q = (0, 2, 1) y R = (- 1, −1, 0) en forma estándar y general.
Solución:
Para escribir una ecuación para un plano, debemos encontrar un vector normal para el plano. Comenzamos identificando dos vectores en el plano:
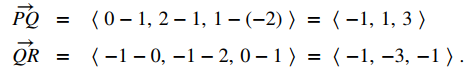
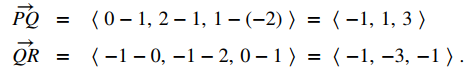
El producto cruz PQ × QR es ortogonal a ambos PQ y QR, por lo que es normal al plano que contiene estos dos vectores:
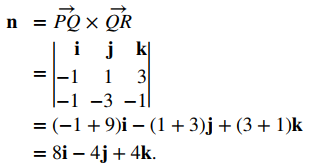
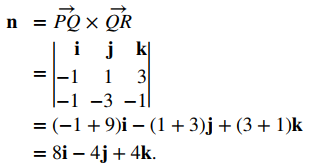
Por lo tanto, n = ⟨8, −4, 4⟩, y podemos elegir cualquiera de los tres puntos dados para escribir una ecuación del plano:
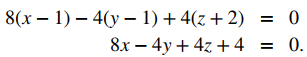
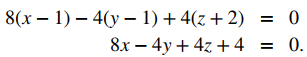
Las ecuaciones escalares de un plano varían según el vector normal y el punto elegido.
EJEMPLO ILUSTRATIVO 10.5_6. Escribir una ecuación para un plano dado un punto y una recta
Encuentre una ecuación del plano que pasa por el punto (1, 4, 3) y contiene la recta dada por x = (y − 1)/2 = z + 1.
Solución:
Las ecuaciones simétricas describen la recta que pasa a través del punto (0, 1, −1) paralelo al vector v1 = ⟨1, 2, 1⟩ (ver la siguiente figura). Use este punto y el punto dado, (1, 4, 3), para identificar un segundo vector paralelo al plano:
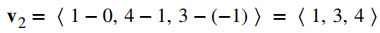
Use el producto cruz de estos vectores para identificar un vector normal para el plano:
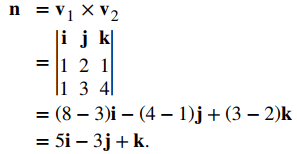
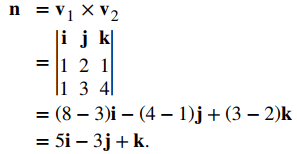
Las ecuaciones escalares para el plano son
5x − 3 (y − 1) + (z + 1) = 0 y 5x − 3y + z + 4 = 0.

Ahora que podemos escribir una ecuación para un plano, podemos usar la ecuación para encontrar la distancia d entre un punto P y el plano. Se define como la distancia más corta posible desde P hasta un punto en el plano.


Así como encontramos la distancia bidimensional entre un punto y una recta calculando la longitud de un segmento de recta perpendicular a la recta, encontramos la distancia tridimensional entre un punto y un plano calculando la longitud de un segmento de recta perpendicular al plano. Deje que R sea el punto en el plano de modo que el vector RP sea ortogonal al plano, y deje que Q sea un punto arbitrario en el plano. Luego, la proyección del vector QP sobre el vector normal describe el vector RP, como se muestra en la Figura 10.5_7.
TEOREMA 10.5_3. La distancia entre un plano y un puntoSuponga que un plano con el vector normal n pasa a través del punto Q. La distancia d desde el plano hasta un punto P que no está en el plano viene dada por
|
EJEMPLO ILUSTRATIVO 10.5_7. Distancia entre un punto y un plano
Encuentre la distancia entre el punto P = (3, 1, 2) y el plano dado por x − 2y + z = 5 (vea la siguiente figura).
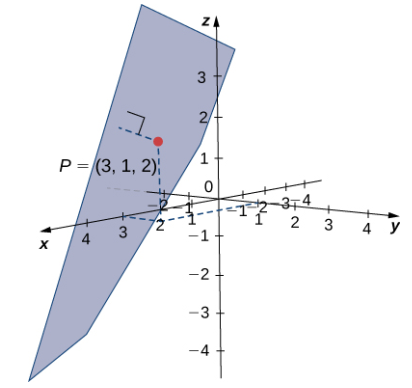

Solución:
Los coeficientes de la ecuación del plano proporcionan un vector normal para el plano: n = ⟨1, −2, 1⟩. Para encontrar el vector QP, necesitamos un punto en el plano. Cualquier punto funcionará, así que configure y = z = 0 para ver que el punto Q = (5, 0, 0) se encuentra en el plano. Encuentre la forma componente del vector de Q a P:
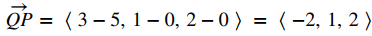
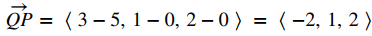
Aplique la fórmula de distancia entre un punto y un plano:
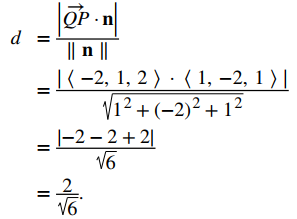
Planos paralelos e intersecantes
Hemos discutido las diversas relaciones posibles entre dos rectas en dos dimensiones y tres dimensiones. Cuando describimos la relación entre dos planos en el espacio, solo tenemos dos posibilidades: los dos planos distintos son paralelos o se intersecan. Cuando dos planos son paralelos, sus vectores normales son paralelos. Cuando dos planos se cruzan, la intersección es una recta (Figura 10.5_8).
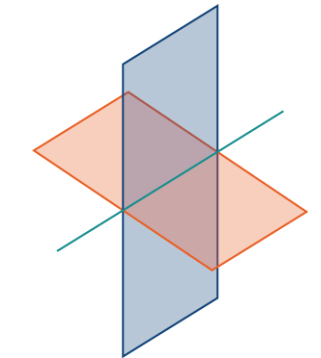

EJEMPLO ILUSTRATIVO 10.5_8. Encontrar la recta de intersección para dos planos
Encuentre ecuaciones paramétricas y simétricas para la recta formada por la intersección de los planos dados por x + y + z = 0 y 2x − y + z = 0 (vea la siguiente figura).
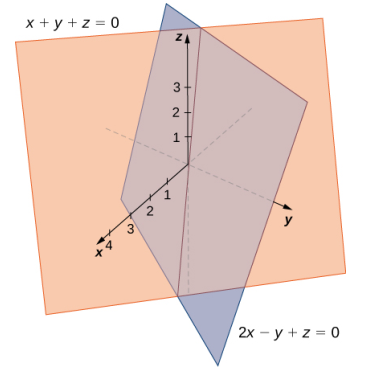

Solución:
Tenga en cuenta que los dos planos tienen normales no paralelas, por lo que los planos se intersecan. Además, el origen satisface cada ecuación, por lo que sabemos que la recta de intersección pasa a través del origen. Sume las ecuaciones planas para que podamos eliminar una de las variables, en este caso, y:
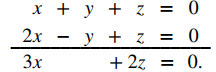
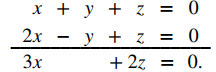
Esto nos da x = −(2/3)z. Sustituimos este valor en la primera ecuación para expresar y en términos de z:
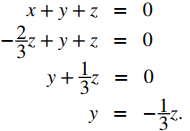
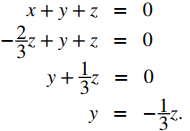
Ahora tenemos las dos primeras variables, x e y, en términos de la tercera variable, z. A continuación definimos z en términos de t. Para eliminar la necesidad de fracciones, elegimos definir el parámetro t como t = −(1/3)z. Entonces, z = −3t. Al sustituir la representación paramétrica de z en las otras dos ecuaciones, vemos que las ecuaciones paramétricas para la recta de intersección son x = 2t, y = t, z = −3t. Las ecuaciones simétricas para la recta son x/2 = y = z/(− 3).
Además de encontrar la ecuación de la recta de intersección entre dos planos, es posible que necesitemos encontrar el ángulo formado por la intersección de dos planos. Por ejemplo, los ingenieros que construyen una casa necesitan saber el ángulo donde se encuentran las diferentes secciones del techo para saber si el techo se verá bien y se drenará correctamente. Podemos usar vectores normales para calcular el ángulo entre los dos planos. Podemos hacer esto porque el ángulo entre los vectores normales es el mismo que el ángulo entre los planos. La figura 10.5_9 muestra por qué esto es cierto.
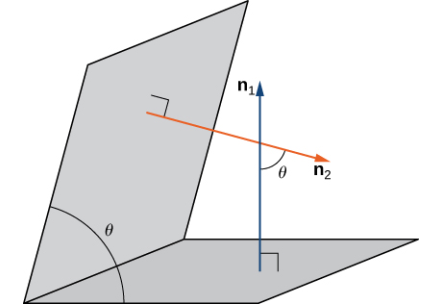

Podemos encontrar la medida del ángulo θ entre dos planos de intersección al encontrar primero el coseno del ángulo, usando la siguiente ecuación:
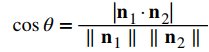
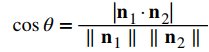
Entonces podemos usar el ángulo para determinar si dos planos son paralelos u ortogonales o si se cruzan en algún otro ángulo.
EJEMPLO ILUSTRATIVO 10.5_9. Encontrar el ángulo entre dos planos
Determine si cada par de planos es paralelo, ortogonal o ninguno. Si los planos se intersecan, pero no son ortogonales, encuentre la medida del ángulo entre ellos. Da la respuesta en radianes y redondea a dos decimales.
a) x + 2y − z = 8 y 2x + 4y − 2z = 10
b) 2x − 3y + 2z = 3 y 6x + 2y − 3z = 1
c) x + y + z = 4 y x − 3y + 5z = 1
Solución:
a) Los vectores normales para estos planos son n1 = ⟨1, 2, −1⟩ y n2 = ⟨2 ,4, −2⟩. Estos dos vectores son múltiplos escalares entre sí. Los vectores normales son paralelos, por lo que los planos son paralelos.
b) Los vectores normales para estos planos son n1 = ⟨2, −3, 2⟩ y n2 = ⟨6, 2, −3⟩. Tomando el producto punto de estos vectores, tenemos
![]()
![]()
Los vectores normales son ortogonales, por lo que los planos correspondientes también son ortogonales.
c) Los vectores normales para estos planos son n1 = ⟨1, 1 ,1⟩ y n2 = ⟨1, −3, 5⟩:
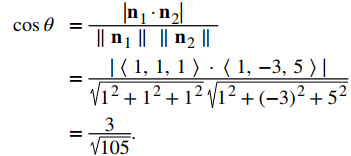
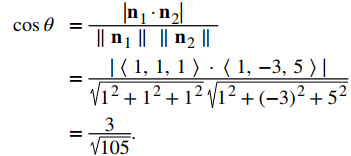
El ángulo entre los dos planos es 1.27 rad, o aproximadamente 73°.
Cuando descubrimos que dos planos son paralelos, es posible que necesitemos encontrar la distancia entre ellos. Para encontrar esta distancia, simplemente seleccionamos un punto en uno de los planos. La distancia desde este punto al otro plano es la distancia entre los planos.
Anteriormente, presentamos la fórmula para calcular esta distancia con la ecuación:
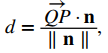
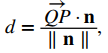
donde Q es un punto en el plano, P es un punto que no está en el plano y n es el vector normal que pasa por el punto Q. Considere la distancia desde el punto (x0, y0, z0) al plano ax + by + cz + k = 0. Sea (x1, y1, z1) cualquier punto del plano. Sustituyendo en la fórmula se obtiene
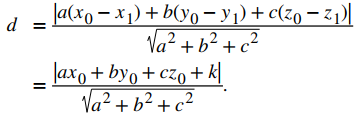
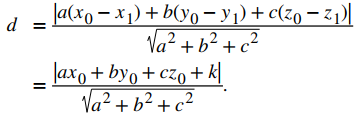
Establecemos este resultado formalmente en el siguiente teorema.
TEOREMA 10.5_4. Distancia desde un punto a un planoSea P (x0, y0, z0) un punto. La distancia de P al plano ax + by + cz + k = 0 viene dada por
|
EJEMPLO ILUSTRATIVO 10.5_10. Encontrar la distancia entre planos paralelos
Encuentre la distancia entre los dos planos paralelos dados por 2x + y − z = 2 y 2x + y − z = 8.
Solución:
El punto (1, 0, 0) se encuentra en el primer plano. La distancia buscada, entonces, es
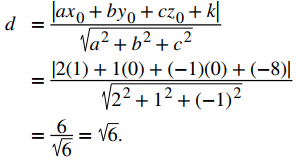
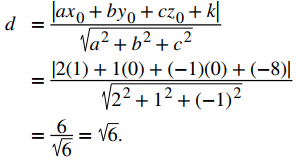

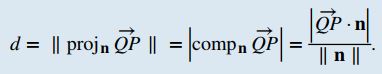
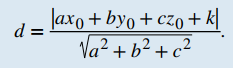
y si me dan la distancia entre esos dos puntos para que la necesito? Debo usarla para resolver la ecuación algebraica?
Un aporte muy interesante. Gracias por la información. Saludos.
Con gusto, bienvenida! 👍😺
Wow eso fue extraño. Acabo de escribir un comentario increíblemente largo, pero después de hacer clic en enviar, mi comentario no apareció. Grrrr … bueno, no voy a escribir todo eso otra vez. De todos modos, solo quería decir blog fantástico!
jajaja, a veces suceden esos inconvenientes, gracias por tomarte el tiempo en escribir.