Distancia entre un punto y una recta
Ya sabemos cómo calcular la distancia entre dos puntos en el espacio. Ahora ampliamos esta definición para describir la distancia entre un punto y una recta en el espacio. Existen varios contextos del mundo real cuando es importante poder calcular estas distancias. Al construir una casa, por ejemplo, los constructores deben considerar los requisitos de “retroceso”, cuando las estructuras o los accesorios deben estar a una cierta distancia de la línea de la propiedad. Los viajes aéreos ofrecen otro ejemplo. Las aerolíneas están preocupadas por las distancias entre las áreas pobladas y las rutas de vuelo propuestas.
Sea L una recta en el plano y sea M cualquier punto que no esté en la recta. Luego, definimos la distancia d de M a L como la longitud del segmento de recta MP, donde P es un punto en L tal que MP es perpendicular a L (Figura 10.5_1).
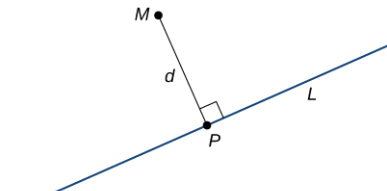
Figura 10.5_1 La distancia desde el punto M hasta la recta L es la longitud del segmento MP.
Cuando buscamos la distancia entre una recta y un punto en el espacio, también se aplica la figura 10.5_1. Todavía definimos la distancia como la longitud del segmento de recta perpendicular que conecta el punto con la recta. En el espacio, sin embargo, no hay una manera clara de saber qué punto de la recta crea un segmento de recta tan perpendicular, por lo que seleccionamos un punto arbitrario en la recta y utilizamos las propiedades de los vectores para calcular la distancia. Por lo tanto, sea P un punto arbitrario en la línea L y sea v un vector de dirección para L (Figura 10.5_2).
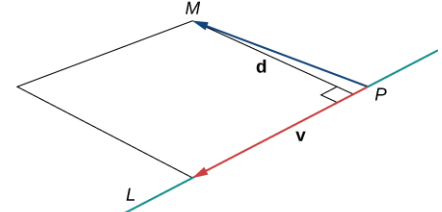

De acuerdo con el área de un paralelogramo, los vectores
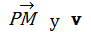
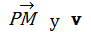
forman dos lados de un paralelogramo con área
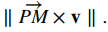
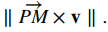
Usando una fórmula de geometría, el área de este paralelogramo también se puede calcular como el producto de su base y altura:
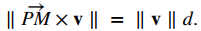
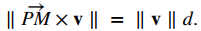
Podemos usar esta fórmula para encontrar una fórmula general para la distancia entre una recta en el espacio y cualquier punto que no esté en la recta.
TEOREMA 10.5_2. Distancia de un punto a una rectaSea L una recta en el espacio que pase por el punto P con el vector de dirección v. Si M es cualquier punto que no esté en L, entonces la distancia de M a L es
|
EJEMPLO ILUSTRATIVO 10.5_3. Calcular la distancia de un punto a una recta
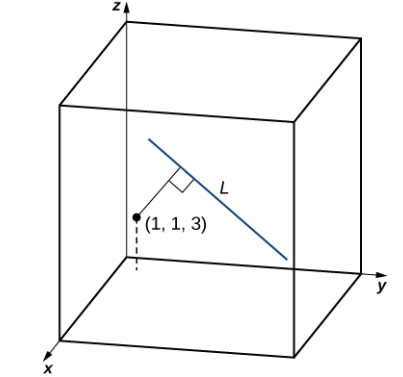
Encuentre la distancia entre el punto M = (1, 1, 3) y la recta (x − 3)/4 = (y + 1)/2 = z − 3.
Solución:
A partir de las ecuaciones simétricas de la recta, sabemos que el vector v = ⟨4, 2, 1⟩ es un vector de dirección para la recta. Al establecer las ecuaciones simétricas de la rect igual a cero, vemos que el punto P (3, -1, 3) se encuentra en la recta. Luego,
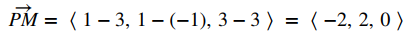
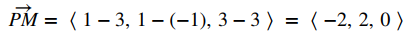
Para calcular la distancia, necesitamos encontrar
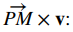
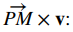


Por lo tanto, la distancia entre el punto y la recta es (Figura 10.5_3)



Relaciones entre rectas
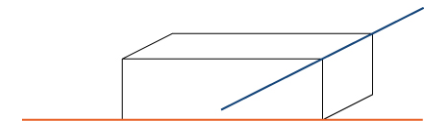
Dadas dos rectas en el plano bidimensional, las rectas son coincidentes, son paralelas pero no coincidentes, o se intersectan en un solo punto. En tres dimensiones, es posible un cuarto caso. Si dos rectas en el espacio no son paralelas, pero no se cruzan, entonces se dice que las rectas son rectas oblicuas (Figura 10.5_4).

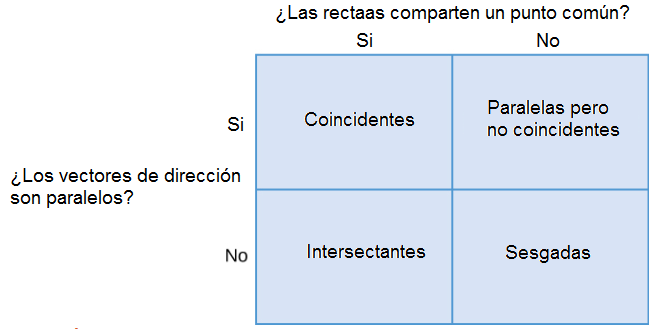
Para clasificar las rectas como paralelas pero no coincidentes, coincidentes, intersecantes o sesgadas, necesitamos saber dos cosas: si los vectores de dirección son paralelos y si las rectas comparten un punto (Figura 10.5_5).

EJEMPLO ILUSTRATIVO 10.5_4. Clasificación de rectas en el espacio
Para cada par de rectas, determine si las rectas son coincidentes, paralelas pero no coincidentes, sesgadas o interceptadas.
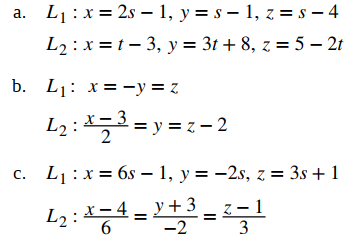
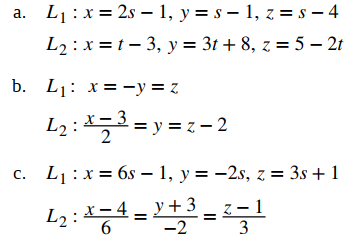
Solución:
a. La recta L1 tiene el vector de dirección v1 = ⟨2, 1, 1⟩; la recta L2 tiene el vector de dirección v2 = ⟨1, 3, −2⟩. Debido a que los vectores de dirección no son vectores paralelos, las rectas se intersecan o se sesgan. Para determinar si las rectas se cruzan, vemos si hay un punto, (x, y, z), que se encuentra en ambas rectas. Para encontrar este punto, usamos las ecuaciones paramétricas para crear un sistema de ecuaciones:
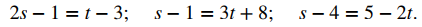
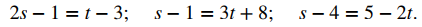
Por la primera ecuación, t = 2s + 2. Sustituyendo en la segunda ecuación se obtiene
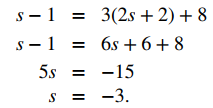
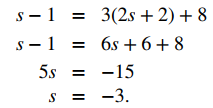
La sustitución en la tercera ecuación, sin embargo, produce una contradicción:
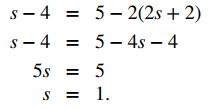
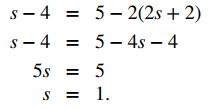
No existe un punto único que satisfaga las ecuaciones paramétricas para L1 y L2 simultáneamente. Estas rectas no se intersectan, por lo que son asimétricas (consulte la siguiente figura).


b. La recta L1 tiene el vector de dirección v1 = ⟨1, −1, 1⟩ y pasa a través del origen, (0, 0, 0). La recta L2 tiene un vector de dirección diferente, v2 = ⟨2, 1, 1⟩, por lo que estas rectas no son paralelas o coincidentes. Supongamos que r representa el parámetro para la recta L1 y que s representa el parámetro para L2:
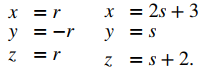
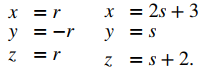
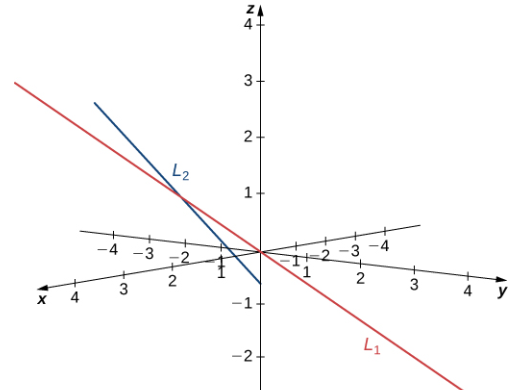
Resuelve el sistema de ecuaciones para encontrar r = 1 y s = −1. Si necesitamos encontrar el punto de intersección, podemos sustituir estos parámetros en las ecuaciones originales para obtener (1, −1, 1) (ver la siguiente figura).

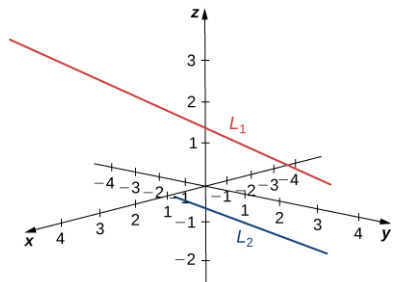
c. Las rectas L1 y L2 tienen vectores de dirección equivalentes: v = ⟨6, −2, 3⟩. Estas dos rectas son paralelas (ver la siguiente figura).


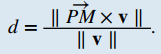
y si me dan la distancia entre esos dos puntos para que la necesito? Debo usarla para resolver la ecuación algebraica?
Un aporte muy interesante. Gracias por la información. Saludos.
Con gusto, bienvenida! 👍😺
Wow eso fue extraño. Acabo de escribir un comentario increíblemente largo, pero después de hacer clic en enviar, mi comentario no apareció. Grrrr … bueno, no voy a escribir todo eso otra vez. De todos modos, solo quería decir blog fantástico!
jajaja, a veces suceden esos inconvenientes, gracias por tomarte el tiempo en escribir.