Continuidad

Continuidad sobre un intervalo

Ahora que hemos explorado el concepto de continuidad en un punto, extendemos esa idea a la continuidad durante un intervalo. A medida que desarrollamos esta idea para diferentes tipos de intervalos, puede ser útil tener en cuenta la idea intuitiva de que una función es continua durante un intervalo si podemos usar un lápiz para rastrear la función entre dos puntos en el intervalo sin levantar el Lápiz del papel. En preparación para definir la continuidad en un intervalo, comenzamos mirando la definición de lo que significa que una función sea continua desde la derecha en un punto y continua desde la izquierda en un punto.

CONTINUIDAD DESDE LA DERECHA Y DESDE LA IZQUIERDA

Se dice que una función f (x) es continua desde la derecha en a si limx → a+ f (x) = f (a). Se dice que una función f (x) es continua desde la izquierda en a si limx → a− f (x) = f (a).

Una función es continua durante un intervalo abierto si es continua en cada punto del intervalo. Una función f (x) es continua durante un intervalo cerrado de la forma [a, b] si es continua en cada punto de (a, b) y es continua desde la derecha en a y es continua desde la izquierda en b. Análogamente, una función f (x) es continua durante un intervalo de la forma (a, b] si es continua sobre (a, b) y es continua desde la izquierda en b. La continuidad sobre otros tipos de intervalos se define en un moda similar.

Requerir que lim_{x → a+} f (x) = f (a) y lim_{x → b−} f (x) = f (b) asegura que podamos rastrear la gráfica de la función desde el punto (a, f (a)) hasta el punto (b, f (b)) sin levantar el lápiz. Si, por ejemplo, lim_{x → a+} f (x) ≠ f (a), tendríamos que levantar nuestro lápiz para saltar de f (a) a la gráfica del resto de la función sobre (a, b].

EJEMPLO 2.4_8. Continuidad en un intervalo

Indique los intervalo(s) durante los cuales la función

Es continua.

Solución:
Ya que

es una función racional, es continua en cada punto de su dominio. El dominio de f (x) es el conjunto (−∞, −2) ∪ (−2, 0) ∪ (0, + ∞). Por lo tanto, f (x) es continua en cada uno de los intervalos (−∞, −2), (- 2, 0) y (0, + ∞).

EJEMPLO 2.4_9. Continuidad sobre un intervalo

Indique los intervalo(s) durante los cuales la función

Es continua.

Solución:

De las leyes límite, sabemos que

para todos los valores de a en (−2, 2). También sabemos que

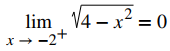
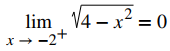
existe y

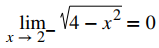
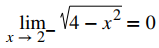
existe Por lo tanto, f (x) es continua durante el intervalo [−2, 2].

El teorema de la función compuesta nos permite ampliar nuestra capacidad para calcular límites. En particular, este teorema en última instancia nos permite demostrar que las funciones trigonométricas son continuas sobre sus dominios.

TEOREMA 2.4.2 Teorema de la función compuesta

Si f (x) es continua en L y entonces

Antes de pasar al ejemplo 2.4_10, recuerde que anteriormente, en la sección sobre leyes de límites, mostramos lim_{x → 0} cosx = 1 = cos (0). En consecuencia, sabemos que f (x) = cosx es continuo en 0. En el ejemplo 2.4_10 vemos cómo combinar este resultado con el teorema de la función compuesta.

EJEMPLO 2.4_10. Límite de una función de coseno compuesto

Evaluar

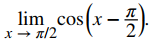
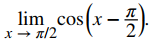
Solución:
La función dada es un compuesto de cosx  y  x − π/2. Ya que

y cosx es continuo en 0, podemos aplicar el teorema de la función compuesta. Así,

La prueba del siguiente teorema utiliza el teorema de la función compuesta, así como la continuidad de f (x) = senx y g(x) = cosx en el punto 0 para mostrar que las funciones trigonométricas son continuas en todos sus dominios.

TEOREMA 2.4.3 Continuidad de funciones trigonométricas

Las funciones trigonométricas son continuas en todos sus dominios.

Prueba Comenzamos demostrando que cosx es continuo en cada número real. Para hacer esto, debemos mostrar que limx → a cosx = cosa para todos los valores de a. La prueba de que senx es continua en cada número real es análoga. Debido a que las funciones trigonométricas restantes pueden expresarse en términos de senx y cosx, su continuidad se deriva de la ley de límite de un cociente.

 

Como puede ver, el teorema de la función compuesta es invaluable para demostrar la continuidad de las funciones trigonométricas. A medida que continuamos nuestro estudio del cálculo, revisamos este teorema muchas veces.

El teorema del valor intermedio

Las funciones que son continuas en intervalos de la forma [a, b], donde a y b son números reales, exhiben muchas propiedades útiles. A lo largo de nuestro estudio de cálculo, encontraremos muchos teoremas poderosos sobre tales funciones. El primero de estos teoremas es el teorema del valor intermedio.

TEOREMA 2.4.4 El teorema del valor intermedio

Sea f una función continua en un intervalo cerrado y acotado [a, b]. Si z es cualquier número real entre f (a) y f (b), entonces hay un número c en [a, b] que satisface f (c) = z en la Figura 2.4_7. Figura 2.4.7 Hay un número c ∈ [a, b] que satisface f (c) = z.

EJEMPLO 2.4_11. Aplicación del teorema del valor intermedio

Demuestre que f (x) = x − cosx tiene al menos un cero.

Solución:
Dado que f (x) = x − cosx es continua sobre (−∞, + ∞), a su vez, es continua sobre cualquier intervalo cerrado de la forma [a, b]. Si puede encontrar un intervalo [a, b] tal que f (a) y f (b) tengan signos opuestos, puede usar el Teorema del valor intermedio para concluir que debe haber un número real c en (a, b) que satisfaga f (c) = 0. Tenga en cuenta que

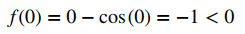
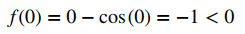
y

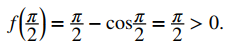
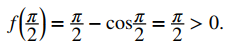
Usando el teorema del valor intermedio, podemos ver que debe haber un número real c en [0, π / 2] que satisfaga f (c) = 0. Por lo tanto, f (x) = x − cosx tiene al menos un cero.

EJEMPLO 2.4_12. ¿Cuándo puede aplicar el teorema del valor intermedio?

Si f (x) es continua sobre [0, 2], f (0) > 0 y f (2) > 0, ¿podemos usar el Teorema del valor intermedio para concluir que f (x) no tiene ceros en el intervalo [0 , 2]? Explique.

Solución:
No. El teorema del valor intermedio solo nos permite concluir que podemos encontrar un valor entre f (0) y f (2); no nos permite concluir que no podemos encontrar otros valores. Para ver esto más claramente, considere la función f (x) = (x − 1)². Satisface f (0) = 1 > 0, f (2) = 1 > 0 y f (1) = 0.

EJEMPLO 2.4_13. ¿Cuándo puede aplicar el teorema del valor intermedio?

Para f (x) = 1 / x, f (−1) = – 1 < 0  y  f (1) = 1 > 0. ¿Podemos concluir que f (x) tiene un cero en el intervalo [−1, 1]?

Solución:
No. La función no es continua sobre [−1, 1]. El teorema del valor intermedio no se aplica aquí.

Ejercicios resueltos